3.9. Теорема об изменении кинетического момента механической системы относительно центра и оси

1. Теорема моментов относительно центра.

Производная по времени от кинетического момента механической системы относительно некоторого неподвижного центра равна геометрической сумме моментов всех внешних сил, действующих на систему, относительно того же центра.

Доказательство.

Для точки системы . Выполняя суммирование по всем точкам системы, получим , где ; — главный момент внешних сил относительно центра ; — по свойству внутренних сил.

(3.34)

Следствие. Если главный момент внешних сил относительно некоторого центра равен нулю, то кинетический момент системы относительно этого центра не изменяется (закон сохранения кинетического момента).

2. Теорема моментов относительно оси.

Производная по времени от кинетического момента механической системы относительно некоторой неподвижной оси равна сумме моментов всех внешних сил, действующих на систему, относительно этой оси.

Доказательство. Спроектируем векторное равенство (3.34) на оси декартовых координат, получим

, , (3.35)

где , , — кинетические моменты механической системы относительно осей координат; , , — главные моменты внешних сил относительно осей координат.

Следствие. Если главный момент внешних сил относительно некоторой оси равен нулю, то кинетический момент системы относительно этой оси не изменяется.

Н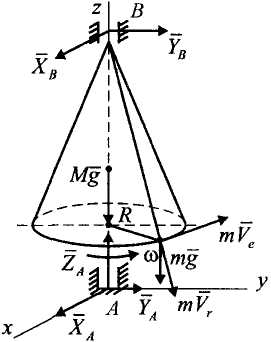 апример, , тогда .

Пример 9.

Используя условие примера 7, определить угловую скорость вращения конуса в момент, когда материальная точка будет находиться на основании конуса, если в начальный момент она находилась в вершине конуса, а его угловая скорость . Масса точки , масса конуса .

Рисунок 18

ешение. Внешними силами, действующими на механическую систему (конус + материальная точка), являются силы тяжести конуса и точки, реакции подпятника —