Раздел 3. Динамика.

Тема 3. Общие теоремы динамики материальной точки и механической системы (часть 1)

3.1. Теорема о движении центра масс системы

Теорема. Центр масс механической системы движется как любая материальная точка, масса которой равна массе всей механической системы и к которой приложена сила, равная главному вектору внешних сил.

Доказательство.

Основное уравнение динамики для материальной точки . Для всей механической системы

, (3.1)

где — по свойству внутренних сил; — главный вектор всех внешних сил, приложенных к системе;

.

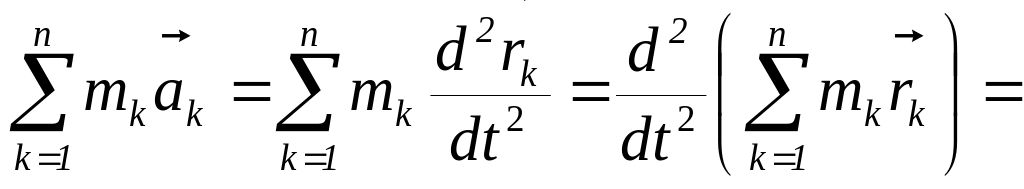
С учетом этого (3.1) примет вид

(3.2)

Уравнение (3.2) может быть записано в скалярной форме в проекциях на оси декартовых координат или на естественные оси. В декартовых осях (3.2) имеет вид

, , , . (3.3)

Следствия из теоремы:

1. Если главный вектор внешних сил, действующих на систему, равен нулю, то центр масс механической системы движется равномерно и прямолинейно либо покоится.

2. Если проекция главного вектора внешних сил, действующих на систему, на какую-либо ось равна нулю, то проекция центра масс на эту ось либо покоится, либо движется равномерно, т. е., например, если 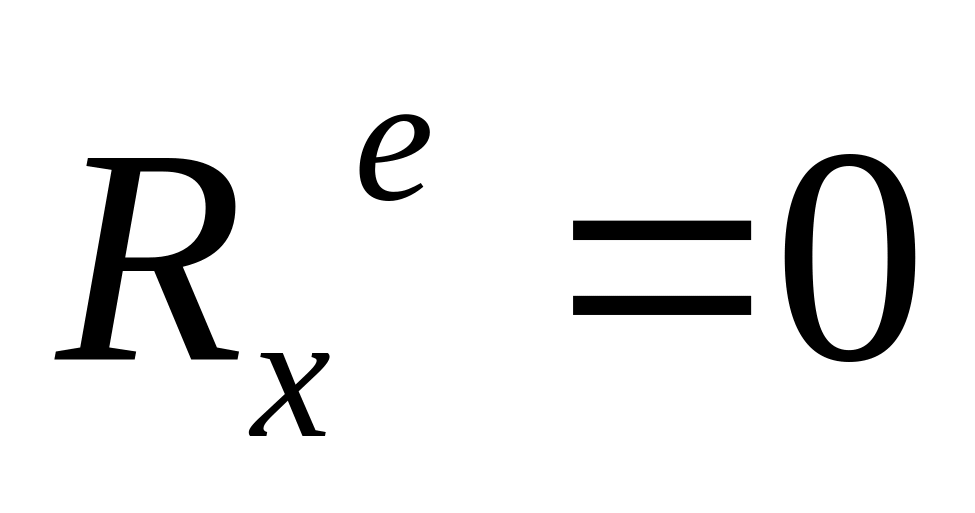, то .

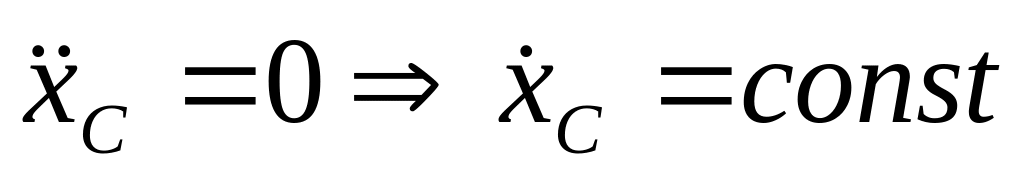Если в начальный момент система покоилась, то — проекция центра масс покоится. При центр масс будет двигаться вдоль оси с постоянной скоростью.

Эти следствия выражают закон сохранения движения центра масс механической системы. При справедливо равенство

, (4.3)

где — приращение координаты центра масс тела при изменении положения тел в механической системе, равное проекции абсолютного перемещения этой точки на ось .

Пример 1.

К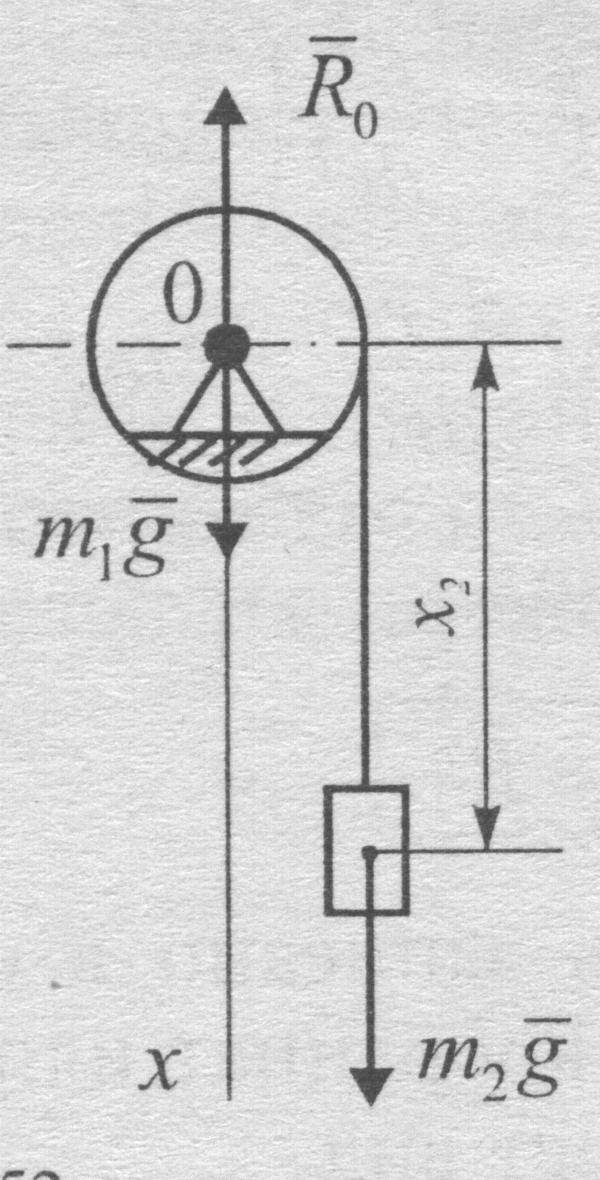 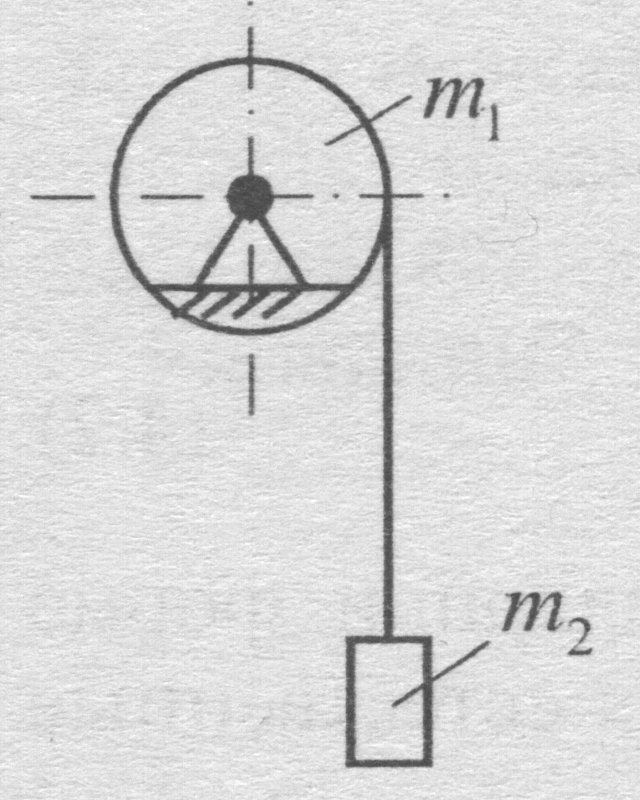концу троса, навитого на барабан, подвешен груз массы . Барабан массы может вращаться вокруг горизонтальной оси. Определить реакцию оси, если груз начнет двигаться с постоянным ускорением (рис. 1, а).

Р

Рисунок 1, а, б

ешение. Покажем внешние силы — вес барабана , вес груза , реакцию оси (рис. 1, б). Запишем теорему о движении центра масс механической системы: . Выберем начало оси в точке и направим ее вниз. Спроектируем векторное равенство на эту ось: . Отсюда . Запишем координату центра масс: , т.к. , а . Продифференцируем дважды, определим ускорение центра масс: . Тогда . Ответ.

П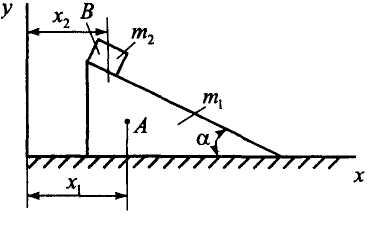 ример 2.

П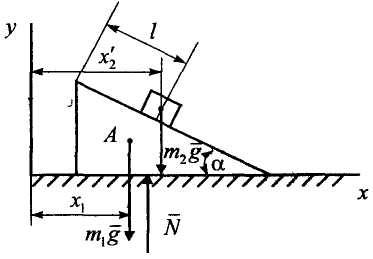 ризма массы покоится на гладкой горизонтальной плоскости. По наклонной плоскости призмы из состояния покоя начинает перемещаться груз массы . Пренебрегая размерами груза, определить перемещение призмы, когда он переместится на расстояние ; (рис. 2, а).

Р

Рисунок 2, а, б

ешение. Внешние силы, действующие на систему: вес призмы, вес груза и нормальная реакция плоскости (рис. 2, б).

Теорема о движении центра масс . Так как (все силы перпендикулярны оси ), то на основании формулы (3.4) , где . .

Ответ: призма переместится влево на .