
- •Функции одной переменной
- •1.Предел последовательности
- •Дайте определение предела последовательности. Докажите, исходя из определения, что .
- •Докажите единственность предела сходящейся последовательности.
- •Докажите ограниченность сходящейся последовательности. Приведите пример ограниченной последовательности, не имеющей предела.
- •Существует ли ? Ответ обоснуйте.
- •Дайте определение функции, непрерывной в точке. Найдите значение , при котором функция является непрерывной в точке .
- •Дайте определение точки разрыва функции. Приведите примеры функций, для которых является: а) точкой разрыва I рода со скачком, равным 2; б) точкой разрыва II рода.
- •Сформулируйте теорему о существовании нуля непрерывной функции. Используя эту теорему, докажите, что уравнение имеет корень на отрезке .
- •Функция определена следующим образом . А) Существует ли ? б) Будет ли функция непрерывной в точке ? Дайте обоснованные ответы.
- •На рисунке изображен график функции .
- •Следует ли из существования производной функции в точке ее непрерывность в этой точке? Ответ обоснуйте.
- •Докажите теорему о производной суммы двух функций.
- •Докажите теорему о производной произведения двух функций.
- •На рисунке изображен график производной функции .
- •Функция такова, что для всех действительных значений , и . Какой из представленных графиков может быть графиком функции ?
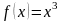 ,
- произвольное число. f ’(x)=3х2
,
- произвольное число. f ’(x)=3х2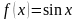 ,
- произвольное число. f ’(x)=cos x
,
- произвольное число. f ’(x)=cos x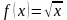 ,
,
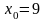 .
f ’(x)=1/(2
.
f ’(x)=1/(2 ),
f ’(x0)=1/6
),
f ’(x0)=1/6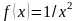 ,
,
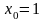 .
f ’(x)= -2 / x3, f ’(x0) = -2
.
f ’(x)= -2 / x3, f ’(x0) = -2 ,
,
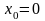 .
|x| не имеет производной в х0=0
.
|x| не имеет производной в х0=0Следует ли из существования производной функции в точке ее непрерывность в этой точке? Ответ обоснуйте.
Если функция U=f(x) дифференцирована в некоторый точке x=x0, то она непрерывна в этой точке. Это условие необходимое, но недостаточное.
Доказательство: пусть функция u= f(x) дифференцирована, тогда существует =а, тогда =а+(x), где (x) – бмп. Тогда y=xа + x(x), y = ( f ’(x0) x +x) = 0 в силу непрерывности.
Докажите теорему о производной суммы двух функций.

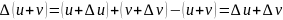
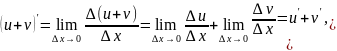
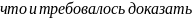
Докажите теорему о производной произведения двух функций.
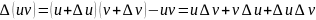
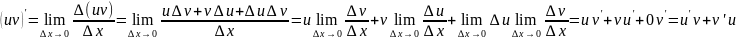
Дайте определение дифференциала функции в точке . Используя дифференциал, найдите приближенное значение величины:
Дифференциалом функции в точке х0 называется главная линейная часть приращения функции в этой точке
При
x0,
dy=y’x
или
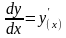 .
.

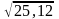 =
=
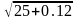 ,
25= x0,
0,12=x
=> f(x)=
,
25= x0,
0,12=x
=> f(x)=
 => f’(x)=1/10
=> f’(x)=1/10
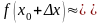 5+0.1*0.12=5.012
5+0.1*0.12=5.012
ln(1+0,09)= ln1+1*0.09=0.09
Дайте определение эластичности функции в точке. Найдите эластичность функции в точке :
Эластичностью
функции y
= f(x)
в точке х0
называется предел
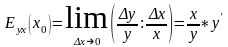 .
.
Ey = (lnx)’ * x
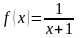 ,
,
 .
Ey
= - x
/ (x+1).
Ey
(4)= -4/5
.
Ey
= - x
/ (x+1).
Ey
(4)= -4/5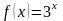 ,
,
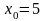 .
Ey
= 3x*ln3*x
/ 3x
= x * ln3. Ey
(5)=5ln3
.
Ey
= 3x*ln3*x
/ 3x
= x * ln3. Ey
(5)=5ln3Дайте определение и сформулируйте необходимое условие локального экстремума функции одной переменной. Приведите пример функции, для которой это условие выполнено в некоторой точке, но экстремум отсутствует.
Точками
локального экстремума явл. точки
локального максимума (минимума). Точкой
локального максимума точка явл. если
существует окрестность т. Мо,
в которой для любой точки М(x,y)
выполняется неравенство f(M)f(M0).
Необходимое условие: если f’(x,y)
имеет частные производные 1-ого порядка
в точке локального экстремума M0(x,y),
то
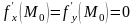 .
Примером является х3,
х0=0
– точка перегиба, но не экстремума.
.
Примером является х3,
х0=0
– точка перегиба, но не экстремума.
На рисунке изображен график производной функции .
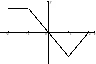
Какое из утверждений верно:
а)
функция
убывает для
 ;
нет
;
нет
б)
функция
возрастает для
 ;
нет, только на х на интервале [-2; 0). Точка
0 – дочка локального максимума.
;
нет, только на х на интервале [-2; 0). Точка
0 – дочка локального максимума.
в)
функция
возрастает для
 ;
нет
;
нет
г) функция имеет локальный минимум при ; нет, максимум
д)
функция
не дифференцируема при
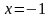 и при
и при
 .
Дифференцируема, так как существует
значение производной.
.
Дифференцируема, так как существует
значение производной.
Функция такова, что для всех действительных значений , и . Какой из представленных графиков может быть графиком функции ?
а) б)

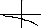
в) г)


д)

Рассмотрим. значит, что ф-ция находится под Ох (то есть ф-ция приминает только отрицательные значения при любом значении аргумента). значит, что функция убывает во всех значениях своего аргумента. И, наконец, означает, что ф-ция вогнута. Всем этим условиям соответствует только б)
Сформулируйте теорему Ролля. Докажите, что производная функции
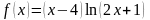 обращается в нуль в некоторой точке
интервала
обращается в нуль в некоторой точке
интервала
 .
.
Пусть
ф-ция f(x)
непрерывна на отрезке [a;b],
дифференцируема на интервале (a;b)
и f(a) = f(b), то найдётся хотя бы одна точка
 ,
в которой
,
в которой .
.
, f(0)=0, f(4)=0. Ф-ция непрерывна и диф-ма на промежутке. В таком случае по теореме Ролля на этом промежутке существует экстремум ф-ции.
Сформулируйте теорему Лагранжа. Докажите, что если
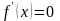 на интервале
на интервале
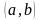 ,
то функция
постоянна на этом интервале.
,
то функция
постоянна на этом интервале.
Пусть
ф-ция f(x)
непрерывна на отрезке [a;b],
дифференцируема на интервале (a;b),
тогда существует точка с О из (a, b) такая,
что f(b) − f(a) = f '(c) · (b − a).
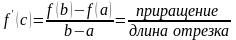 .
=>
.
=>
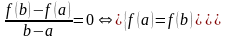 .
.
Используя теорему Лагранжа, докажите, что если
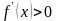 на интервале
,
то функция
возрастает на этом интервале.
на интервале
,
то функция
возрастает на этом интервале.
Пусть функция у=f(x) имеет f’(x)и.непрерывна на отрезке [a, b]; Тогда существует точка такая, что f(b) − f(a) = f '(c) · (b − a).
Пусть функция у=f(x) имеет f’(x)и.непрерывна на отрезке [a, b]; Тогда существует точка такая, что f(b) − f(a) = f '(c) · (b − a)
F'(c)
> 0 ->
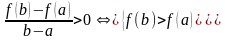 возрастает.
возрастает.
Функция дифференцируема на промежутке
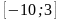 .
Известно, что
.
Известно, что
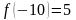 ,
,
 и
и
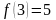 .
.
а) Какое наименьшее количество нулей может иметь данная функция на указанном промежутке? 2 нуля (достаточно отметить точки f(-10) f(-1) и f(3) на графике чтобы это понять)
б)
Существует ли такое значение
 ,
что
,
что
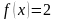 ?
Да, так как существует f(-10)=5
и f(-1)=-1.
Функция непрерывна, и поэтому она должна
проходить в точке f(c)=2.
?
Да, так как существует f(-10)=5
и f(-1)=-1.
Функция непрерывна, и поэтому она должна
проходить в точке f(c)=2.
в) Существуют ли на промежутке у функции горизонтальные касательные? Да, так как она сначала убывает, а потом возрастает. В точке смены убывания на возрастание (f’(x)=0) у функции будет горизонтальная касательная.
г) Если у функции есть только одна точка экстремума на , будет ли она точкой максимума или минимума? Точкой минимума, так как ф-ция меняет свое поведение с убывания на возрастание.
