Если t  0, то:

dp₀/ dt = - p₀ (₁ + ₂) + p₁₁ + p₂₂.

dp₀/ dt= p₁₁ + p₂₂ - p₀ (₁ + ₂) .

Рассуждая аналогичным образом для всех остальных состояний, получаем систему дифференциальных уравнений, описывающих зависимость вероятности каждого состояния от времени:

Теперь можно сформулировать общее правило составления уравнений Колмогорова: в левой части каждого уравнения стоит производная вероятности i-ого состояния. В правой части – сумма произведений вероятностей всех состояний,из которых идут стрелки в данное состояниена интенсивности соответствующих потоков событий,минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-ого) состояния.

Пользуясь этим правилом можно записать уравнения Колмогорова для рассмотренной выше системы отказов блоков системы:

входящие выходящие потоки

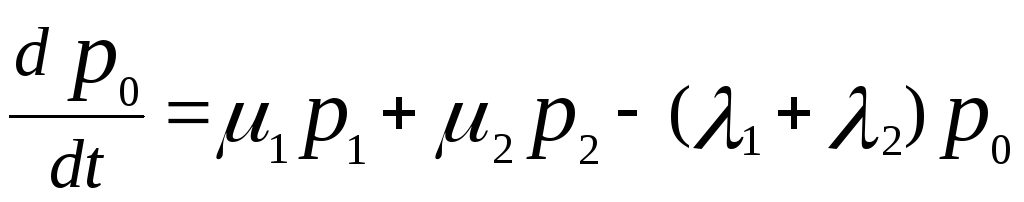
Чтобы решить систему, необходимо задать начальные условия при t= 0. Обычно принимается одна из вероятностей за 1, а остальные равны 0. Для последней системы естественно задать следующие начальные условия:

p₀(0) = 1;p₁(0) =p₂(0) =p₃(0) = 0.

Пример.

Рассмотрим вариант, когда t. Возникает вопрос вероятности состояний стремиться к каким-то пределам. Если эти пределы существуют, то они называютсяфинальными вероятностями состояний. В теории случайных процессов доказывается, что: если числоnсостояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое, то финальные вероятности существуют.

Очевидно, что в сумме они составляют 1. Финальную вероятность состояния S_i можно понимать как среднее относительное время пребывания системы в этом состоянии. Например, система имеет 3 состояния, финальные вероятности которых равны 0,2; 0,3; 0,5. Это значит, что в предельном, стационарном режиме система в среднем 0,2 времени проводит в состоянииS₁, 0,3 – в состоянииS₂и 0,5 в состоянииS₃. Для вычисления финальных вероятностей необходимо левые части уравнений приравнять нулю, т. к. вероятности не изменяются во времени. В результате мы получаем систему алгебраических уравнений:

₁p₁+₂p₂- (₁+₂)p₀= 0 ,

₁p₀+₂p₃- (₂+₁)p₁= 0 ,

₂p₀+₁p₃- (₁+₂)p₂= 0 ,

₂p₁+₁p₂- (₁+₂)p₃= 0 .

Однако в таком виде крайне неудобно вычислять финальные вероятности, т. к. мы имеем однородные уравнения. Введем нормировочное условие:

p₀+p₁+p₂+p₃= 1. При этом любое уравнение можно исключить, т. к. оно вытекает как следствие из остальных.

Зададим для последнего примера численные значения интенсивностей: ₁= 1,₂= 2,₁= 2,₂= 3 и определим финальные вероятности. Пожертвуем четвертым уравнением, добавив вместо него нормировочное условие. Уравнения примут вид:

3p₀ = 2p₁ + 3p₂ ,

4p₁ = p₀ + 3p₃ ,

4p₂ = p₀ + 2p₃ ,

p₀ + p₁ + p₂ + p₃ = 1.

Решая их, получим :

p₀= 0,4 ;p₁= 0,2 ;p₂= 0,27 ;p₃= 0,13 .

Рассмотрим пример составления системы дифференциальных уравнений, описывающих динамику вероятностей состояний для приведенного ранее графа состояний для сонно-бодрой периодики:

Исследуем сначала динамику переходов экспериментально, например, за 1 час.

Получаем:t₁= 0,5 ,t₂= 0,4 ,t₃= 0,1 , гдеt_i- время нахождения объекта вi-ом состоянии.

Далее:n_1-2= 5,n_2-1= 3,n_2-3= 2,n_3-2= 1,n_3-1= 1

Нарисуем последовательность событий во времени (один из вариантов):

1.  2 12121232312 .

Время наблюдения 1 час.

Рассчитаем интенсивность потоков:

₁₂=5/0.5 = 10,₃₁+₃₂= 2/0.1 = 10,₃₁= 10 и₃₂= 10;

₂₁= 3/0.4 =7.5,₂₃= 2/0.4 = 5.

Составим систему дифференциальных уравнений:

Окончательно:

dp₁/dt= - 10p₁+ 7,5p₂+ 10p₃,

dp₂/ dt = 10 p₁ – (7,5 + 5) p₂ + 10 p₃ ,

dp₃/dt = 0  p₁ + 5 p₂ – (10 + 10) p₃ .

Рассчитаем финальные вероятности:

1. левые части приравниваем к0 ,

2. исключаем одно из уравнений, например, 2-ое,

3. добавляем нормированное условие: p₁+p₂+p₃= 1.

П

-10 p₁+ 7,5p₂+ 10p₃= 0,

0 p₁+ 5p₂- 20p₃= 0,

p₁+p₂+p₃= 1.

олучаем систему алгебраических уравнений:

Решив его, получаем финальные вероятности состояний:

,

,,

. Отсюда на основании формулы Крамера: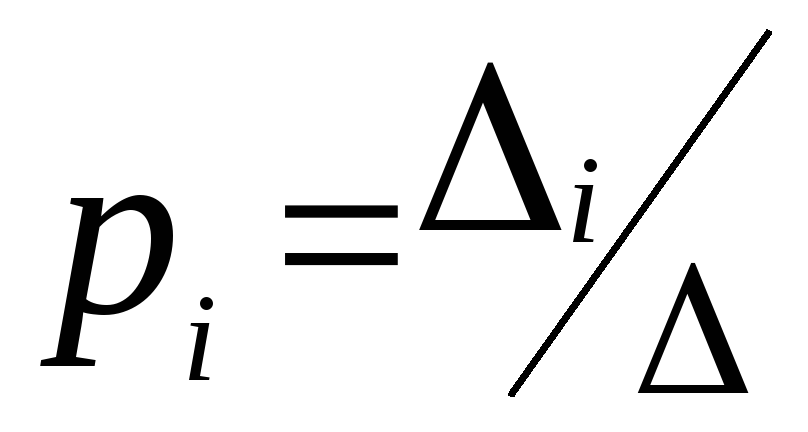, получаем:p₁= 0,44 ,p₂= 0,44 ,p₃= 0,12.

Моделирование систем массового обслуживания с очередями.

Рассмотрим наиболее распространенный случай: n– канальная система массового обслуживания (СМО) с неограниченной очередью.

₁ ₂ _k _k+1 _n _n+1 _n+r

    

S₀ S₁ S_k S_n S_n+1 S_n+r

      2 k(k+1) n nn n

Расшифруем обозначенные состояния:

S₀– в СМО заявок нет (все каналы свободны),

S₁– занят один канал, остальные свободны,

S_k– занятоkканалов, остальные свободны,

S_n– занятоnканалов (все каналы заняты, очереди нет),

S_n+1– заняты всеnканалов, одна заявка в очереди,

S_n+r– заняты всеnканалов,rзаявок стоят в очереди,

Условие существования финальных вероятностей: /n< 1. Если/n1 , то очередь растет до бесконечности.

Для нахождения вероятностей наступления каждого состояния воспользуемся тем же правилом, которое использовалось для расчета коэффициентов СМО без очереди, а именно: в числителе– произведение всех интенсивностей потоков слева направо до данного состояния, взнаменателе– произведение всех интенсивностей потоков справа налево, начиная от данного состояния. Все это отношение умножается наp₀.

,

,

,

.

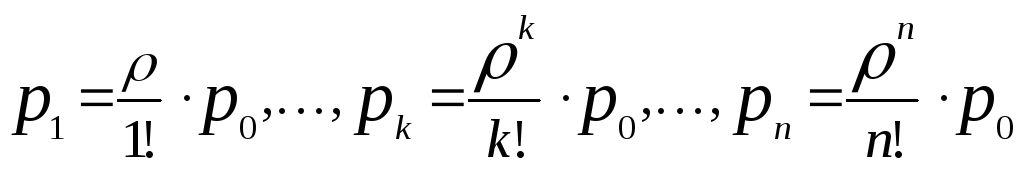Подставим формулы для определения вероятностей (p_k):

,

В скобках мы имеем 2 ряда. Первый из них вычисляется в виде суммы. Второй ряд этосумма бесконечно убывающей геометрической прогрессии.

Общий вид такой прогрессии:

В пределе получается сумма ряда:

Вынесем за скобку в результате:

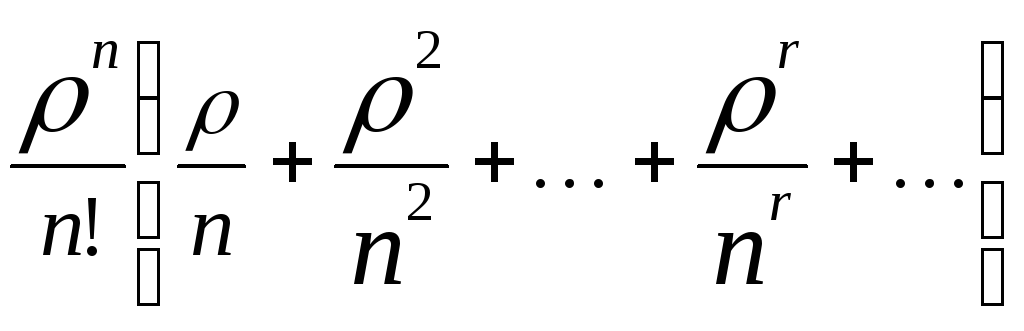- бесконечно убывающая геометрическая прогрессия.

В конечном результате, после ряда преобразований, можно получить формулу Эрланга с очередью:

,

.

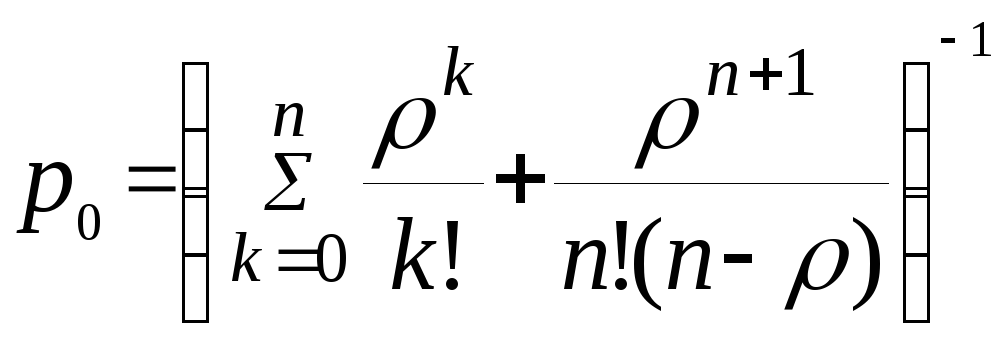В результате вероятность того, что к-ый канал будет занят несколько снижается за счет того, что существует также вероятность появления очереди, а сумма вероятностей по-прежнему равна единице.

Для данной СМО важно рассчитать две общие характеристики ее функционирования: вероятность наличия очереди (р_оч) и среднююдлину очереди (m_s).

. Эта формула после преобразования может быть приведена к более простому виду:

Пример: рассмотрим функционирование поликлиники, которая обслуживает 20000 человек в год.

,, т.е. 12 минут на обслуживание одним врачом.

, таким образом, чтобы очередь не росла, и существовали финальные вероятности, необходимо, чтобы параллельно работало не менее 3 врачей.

В этом случае:

p₁ = 2.65  0.03 = 0.079;

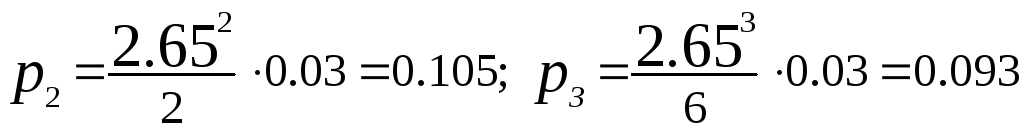
p _оч. = 1(0.03 + 0.079 + 0.105 + 0.093) = 10.307 = 0.693;

Марковские процессы с очередями.

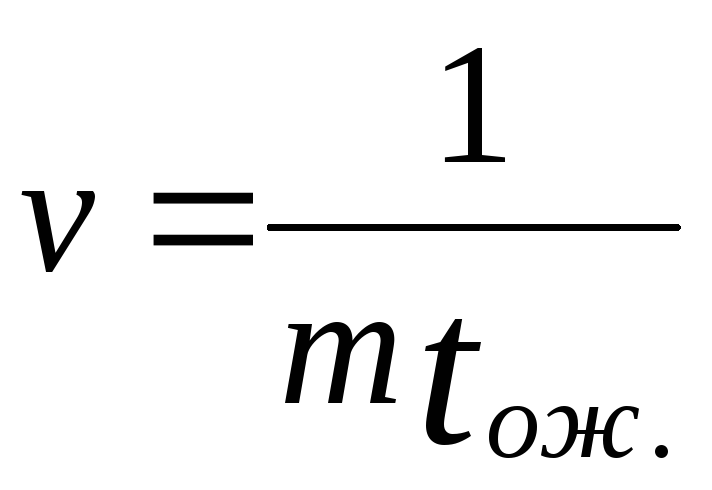 величина, обратная среднему времени ожидания. Это плотность потока ухода заявок, стоящих в очереди.

 вероятность того, что пациент уйдет из системы необслуженным.

 вероятность того, что всеnврачей заняты, аsпациентов ожидают обслуживания.

Пример с очередью:

N= 2000 пациентов в год ;= 0,022;= 0,083 ;n= 1

Показатель установившегося режима:

(;0 с чистым ожиданием )

1. Так как установочный режим существует, то p₀= 0,735;p₁= 0,195.

, 0kn(в этой формуле0),

т. е. согласно этой формулы время обслуживания одного пациента не выходит за пределы возможностей системы. ( < n)

2. Вероятность наличия очереди: p _оч = 1 –p₀–p₁= 0.07

3. Средняя длина очередиm_s= 0,096 человека

Если n= 2:p₀= 0,766 ;p₁= 0,203 ;p₂= 0,026 .

P _оч.= 0.004;m_s= 0,0046 .

N= 20000;= 0,22;= 0,083;= 2,65.

Поэтому для n< 3 не существует стационарного режима с чистым ожиданием. Поэтому характеристики дляn= 3

p₀= 0,03;p₁= 0,078;p₂= 0,104;p₃= 0,092;p _оч.= 0,696;m_s= 5,929.

Система медицинского обслуживания с ограничением длины очереди.

Начальное условие: если очередь оказывается > m, то пациент уходит.

  p₀+p₁= 0;

- - - - - - - - - - - - -

 p_k-1  (  + k ) p_k + ( k + 1)  p_k+1 = 0;

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

 p_n-1  (  + n ) p_n + n  p_n+1 = 0;

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

 p_n+s-1  (  + n ) p_n+s + n  p_n+s+1 = 0;

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

 p_n+m-1  n  p_n+m = 0.

Пример:N= 20000;= 0,22;= 0,083;m= 6.

n= 1:p₀= 0,0007;p₁= 0,0018;p₃= 0,0013;p₄= 0,033;p₅= 0,089;p₆= 0,235;q= 0,377;Q= 0.083.

Относительная пропускная способность: q= 1 –p_n+m, гдеp_n+m– вероятность того, что пациент уйдет необслуженным.

Абсолютная пропускная способность: число обслуживаемых в единицу времени пациентов: Q = q.

Уравнения Колмогорова в задачах массового обслуживания.

Рассмотрим очень широко используемую на практике многоканальную модель обслуживания. (Моделирование многоканальных систем).

Примеры : врачи в больнице, парикмахерская, телеф. сеть, приборы в клинике.

Б

     

  - -   - -  

S₀ S₁ S₂ S_k S_k+1 S_n-1 S_n

   - - - -

 2k(k+1)(n-1)n

лок-схема функционирования такой системы:

Имеют место 2 встречных потока:

  поток заявок (количество заявок в единицу времени, например, пациентов);

  поток, связанный с обслуживанием заявок (1 / m_tобсл.), т.е. количество обслуживаний в единицу времени.

Если использовать рассмотренный ранее принцип построения системы дифференциальных уравнений, то получим следующее:

dp₀ /dt= -p₀+p₁,

dp₁/dt= - (+)p₁+p₀+ 2p₂,

dp₂ /dt = - (2 + ) p₂ +  p₁ + 3 p₃ ,

- - - - - - - - - - - - - - - - - - - - - - - - - -

dp_k / dt =  p_k-1 – ( + k) p_k +  (k + 1) p_k+1,

- - - - - - - - - - - - - - - - - - - - - - - - - -

dp_n / dt = =  p_n-1 -  n p_n .

для одноканальный вход;

для многоканальный поток (путь).

Пример: Больница обслуживает 2000 чел. в год. Работа по 6 часов в день на протяжении 255 дней / год. Единица времени – минута. Один человек обслуживается за 12 мин.

λ = 2000 / 255 660 = 0,022 чел / мин;= 1 / 12 = 0,083 обсл. / мин.

Допустим, что работает один человек:

dp₀ / dt =  0,022  p₀ + 0,083  p₁, 0 =  0,022  p₀ + 0,083  p₁,

dp₁ / dt = 0,022  p₀ - 0,083  p₁. 1 =p₀+p₁.

Решаем систему двух линейных алгебраических уравнений 1-ого порядка:

p₀= 1 –p₁,

 0,022 ( 1 – p₁) + 0,083p₁= 0;p₁( 0,022 + 0,083 ) = 0,022;

p₀= 0,791 – простой,p₁= 0,209 – занятость, т. е. вероятность отказа.

Однако в случае увеличения числа каналов такой подход неэффективен, т. к. необходимо решать системы уравнений высоких порядков. Кроме того, необходимо также вычислить ряд других параметров, например: относительную (Q) и абсолютную (A) пропускную способность, среднее число занятых каналов (K). Важно также определить, имеет ли система финальные вероятности.

В связи с этим выведем формулы для аналитического расчета всех необходимых параметров системы. С этой целью зададим нумерацию интенсивностям. Воспользуемся уравнениями Колмогорова, которые представлены выше для системы массового обслуживания. Возьмем случай для расчета финальных вероятностей, приравняв все производные вероятностей к нулю. В результате:

для 1-ого уравнения:p₀=p₁,

Д

+ (+)p₁=p₀+ 2p₂,

+ p₁+p₁=p₀+ 2p₂.

ля 2-ого уравнения:

Но p₀=p₁ . В результатеp₁= 2p₂.

Д

(2+)p₂=p₁+ 3p₃,

2p₂+p₂=p₁+ 3p₃.

ля 3-ого уравнения:

Но p₁= 2p₂ . В результатеp₂= 3p₃ .

Итак, можно вывести следующую закономерность:

_k+1p_k= (k+ 1)p_k+1

Составляем новую систему уравнений:

p₀ =  p₁

 p₁ = 2 p₂

 p₂ = 3 p₃

- - - - - - - -

 p_k-1 = k p_k

- - - - - - - -

 p_n-1=np_n

Решив эту систему уравнения получим в результате:

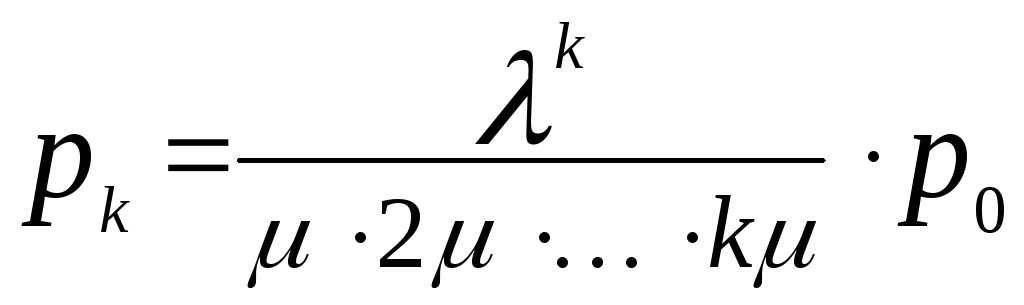
В числителепроизведение всех интенсивностей потоков слева направо до данного состояния, а взнаменателепроизведение всех интенсивностей потоков справа налево, начиная с данного состояния.

Обозначим =λ/μ. Это среднее число заявок, приходящихся на среднее время обслуживания одной заявки (t_обсл/t_заявка)

(< 1) - условие существования финальной вероятности для одноканальной системы.



 < 1 дляn– каналов.

n

В таком случае: .

Определим p₀:p₀+p₁+p₂++p_к++p_n= 1 .

Разделим на p₀левую и правую части.

Отсюда: .

Подставим в это уравнение формулы определения вероятностей:

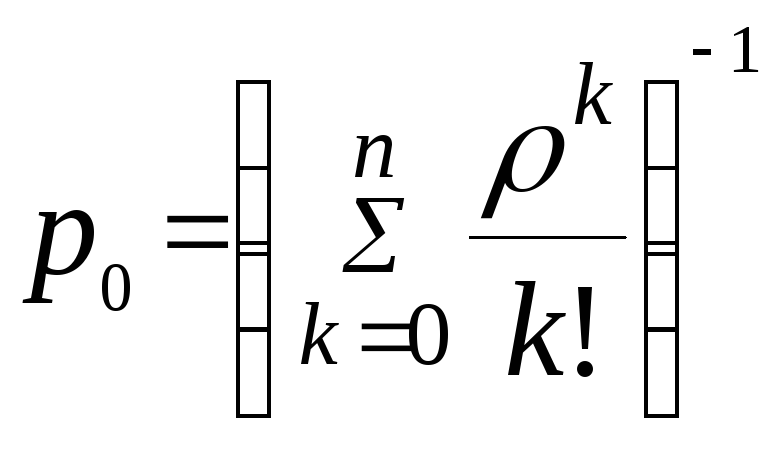
Таким образом финальные вероятности найдены. По ним можно вычислить характеристики эффективности смоделированной СМО.

1. p_отк.вероятность того, что пришедшая заявка получит отказ (не будет обслужена). Для этого нужно, чтобы все каналы были заняты :

p_отк.= p _n = ⁿp₀ /n!

2. Qотносительная пропускная способность – вероятность того, что заявка будет обслужена :

Q= 1p_отк.= 1ⁿp₀ /n!

3) A– абсолютная пропускная способность:

A=Q=(1ⁿp₀ /n!). Если p _отк. = 0, тоA = 

Это есть интенсивность потока обслуженных системой заявок, т. е. количество заявок, обслуженных системой в единицу времени.

4) k– среднее число занятых каналов:

k=A/это означает, что каждый занятый канал в единицу времени обслуживает в среднемзаявок. Поэтому для нахожденияkнеобходимо интенсивность потока обслуживания системы заявок разделить на.

Вернемся к ранее рассмотренному примеру моделирования одноканальной системы обслуживания больных.

Вычислим все параметры системы :

 = λ/ μ = 0,022 / 0,083= 0.265

p₀ = ( 1 +  ) ^–1 = ( 1 + 0.265 ) ^–1 = 0.791 ,

p₁ =   p₀ = 0,265  0,79 = 0,209 .

Эти данные, полученные аналитическим путем по выведенным формулам, совпадают с результатами решения системы уравнений.

Далее:

P _отк.=p_k=p₁= 0,209 .

Q= 1P _отк.= 10,209 = 0,791, относительная пропускная способность (р, что заявка будет обслужена).

A=Q= 0,0220,791 = 0,0174, абсолютная пропускная способность (количество заявок, обслуженных системой в единицу времени)

k=A/= 0,0174 / 0,083 = 0,2, среднее число занятых каналов.