Задача медицинской диагностики как задача распознавания образов

При решении практических задач анализа медицинских и био­логических наблюдений для последующего принятия решения о ди­агностике и прогнозировании состояния исследователю приходит­ся иметь дело с совокупностью одновременно зафиксированных на объекте исследования количественных и качественных признаков (x₁,x₂, …,x_p). Абсолютное большинство этих признаков под­вержено некоторому неконтролируемому разбросу при переходе от одного объекта наблюдения к другому, при изменении состояния одного и того же объекта и т.д. Так, например, исследуя одно­родные (по возрастному и национальному составу) группы паци­ентов с целью оценки воздействия на них некоторым лекарствен­ным препаратом, т.е. ,подразумевая подx₁ ,например, час­тоту сердечного ритма, подx₂-систолическое давление, подx₃ -диастолическое давление и т.д., нетрудно убедиться, что при переходе от одного пациента к другому каждый из признаков имеет некоторый неконтролируемый разброс. Однако для каждого заболевания на однородной группе объектов это варьирование признаков, как правило, подчиняется некоторым общим тенденци­ям и закономерностям как в смысле пределов, так и в смысле зависимости варьирования.

В общем случае постановку задач сбора и накопления медико-биологических данных для последующего принятия решений можно представить в виде схемы (рис.6.2). 3десь осьJотражает последовательность накопления информации о признакахx_j .Ось I отражает накопление объектов исследованияf_i(может быть один и тот же объект в различных состояниях). Осьtхарактеризует возможность изменения и накопления объектов множества F во времени, т.е. учитывает динамические особенности данных объектов исследования. В этом случае совокупность наблюдаемых величин (объектов и призна­ков) может быть представлена в виде матрицы таблицы экспериментальных данных (ТЭД), что позволяет наметить решение основных задач, возникающих при диагностике и прогнози­ровании состояния:

1. Снижение размерности исходного пространства признаков;

2. Разбиение исходных данных на однородные группы;

3. Классификация исходных данных;

4. Принятие решения;

5. Отображение полученных данных.

Структурный подход к обработке экспериментальных данных

Основные трудности при обработке экспериментальных дан­ных связаны, прежде всего, с необходимостью установить достовер­ность тех или иных априорных предположений, принятых иссле­дователями и используемых в том или ином виде в математических моделях, на которых основываются алгоритмы обработки данных.

Именно желание приблизить различные статистические методы анализа данных к исследователю породило огромное количество частных схем решения задач обработки. В тоже время для обоснованного выбора одной схемы при решении конкретной задачи требуются уже знания профессионала в области обработки данных, которыми чаще всего не

Обладает исследователь в предметной области (медик).

В настоящее время методы обработки экспериментальных дан­ных используются все более широким кругом ученых и специали­стов, работающих в разных областях науки и техники. В силу раз­личной специфики исследований в этих областях данные экспе­риментов (испытаний, наблюдений) существуют в различных фор­мах, отличаясь как по уровню формализации (описание на есте­ственном языке, измерение при помощи приборов), так и по спо­собу представления (графический, текстовой, числовой…).

При автоматизации научных исследований данные, прежде всего, должны отражать существующую модель предметной (исследуе­мой) области реального мира. Очевидно, в этом случае структура изучаемого явления должна найти свое отражение в структуре данных, для того чтобы по ней можно было делать выводы о законо­мерностях, присущих реальности. Отметим, что если структура данных (СД) адекватно отражает предметную область реального мира, то на ее основе возможно решение многих исследуемых проб­лем и, наоборот, если данным навязана конкретная, узкая струк­тура, то они могут быть вообще непригодны для анализа. Так, предположив, например, нормальность распределения некоторой характеристики (т. е. ограничив СД заранее нормальным законом), можно прийти к неверным выводам по всему комплексу изучаемых вопросов, если исходное предположение о законе распределения было неверно (такая проблема возникла, например, при обработке психодиагностических данных).

Таким образом, встает задача выявления и исследования струк­туры анализируемых данных. Мы под СД будем понимать (по­скольку анализируются не только количественные, но и качествен­ные, описательные характеристики объектов множества Е) совокупность описаний объектов и отношений между этими описаниями. Будем считать, что характеристики, кото­рыми описываются объекты Е, т. е. множество признаков в ТЭД, адекватно отражают существо решаемой задачи. Тогда исследо­вание СД сводится к анализу пространственной структуры мно­жества точек — образов объектов Е в П - пространстве, поскольку отношения между объектами Е реализуются через значения при­знаков — координат объектов в П^p.

Как правило, целью анализа СД является построение матема­тической модели исследуемого явления в виде функционального, статистического или иного описания. Такая модель позволяет заменить экспериментальные данные как способ представления явления на некоторый более общий закон, из которого исходные данные вытекают уже как частный случай. Следовательно, СД можно рассматривать как пространственное выражение закономер­ностей, которые эти данные представляют, или, иначе, как пред­ставление данных в виде некоторого описания, характеризую­щего расположение объектов Е в П - пространстве.

Поскольку исследуемое явление может описываться несколь­кими различными моделями, анализ СД содержит, как правило, два необходимых этапа.

1. Разбиение множества объектов Е на непересекающиеся классы S₁, …S_k, каждый из которых соответствует определенной модели исследуемого явления или одной части исследуемого явления. Эта задача решается, как правило, методами автоматической клас­сификации или распознавания образов.

2. Поиск законов, описывающих поведение объектов каждого из классов S₁, …S_k. Эта задача может решаться самыми разно­образными методами: например, при помощи регрессионного, факторного анализов; интерполяции, аппроксимации; методов сни­жения размерности и т. д.

Отметим, что вследствие естественной иерархичности струк­туры явлений реального мира иерархической же структурой за­частую обладают и экспериментальные данные, поэтому указанные этапы анализа СД могут повторяться для выявления собственных структур множеств S₁, …S_k и т. д.

Рассмотрим более подробно первый этап анализа СД. На нем для получения разбиения Е следует применить некоторый мате­матический метод (алгоритм) Н. Выбор метода уже сам по себе на­кладывает на данные в пространстве описания некоторую струк­туру (например, метрику), которая может в принципе исказить исходную СД. Различные методы классификации (распознавания) могут давать в результате различные разбиения Е на классы, по­этому встает задача обоснованного выбора либо метода класси­фикации, либо одного из полученных разбиений. Здесь большую роль могут сыграть априорные знания исследователя и его про­фессиональный опыт. Они оказываются, как правило, полезными при анализе разбиения Е при помощи различных математических методов.

Введем подмножества А_i

как субъективную оценку исследователем количества частейlобъ­емом |А_i|, на которое должно быть классифицировано множество Е. Далее введем подмножества S_k, k=1,…, т, где т —объективное ко­личество частей объемом |S_k|, на которое может быть классифици­ровано множество Е с помощью некоторого набора математических правил Н при заданном пространстве описания.

Определение. Под классом будем понимать объединение объектов исследования в подмножество S_kс помощью того или иного выбранного метода. В общем случае состав и количество клас­сов могут изменяться в зависимости от метода обработки, т. е. от выбора решающего правила.

Определение. Под образом А_iбудем понимать объеди­нение объектов множества Е вlгрупп, соответствующих субъек­тивной оценке исследователя.

Таким образом, здесь появляется возможность учета целевой установки, или, более точно, целевой функции исследователя, ко­торую определим как проблему согласования классификации S_kс ее полезностью с точки зрения «учителя» без каких-либо ап­риорных добавлений к исходной совокупности сведений.

Итак, основным математическим аспектом решения, исходя из определений, является поиск допустимого алгоритма (системы алгоритмов) при согласованииA_i и S_k.

Для уяснения ролиA_i, рассмотрим варианты возможной взаимо­связи междуA_iи S_k:

1. образы разделяются полностью:

, , приi  j;

2. образы имеют области пересечения:

, приi  j;

Первая ситуация возникает в следующих случаях:

(6.1)

(6.2)

Более сложная вторая ситуация отражается соотношением

(6.3)

Случай (6.1) соответствует частному случаю, когда правило принятия решения удовлетворяет исследователя и на основе выбран­ного математического аппарата обеспечивает взаимно однозначную связь между классами и образами.

Случай (6.2) является более сложным вариантом, пока­зывающим необходимость компоновки образа из различных клас­сов. Этот случай указывает на всегда имеющуюся возможность введения аппроксимаций высшего порядка, которые в принципе могут отражать собой более глубокую дифференциацию данных, чем это необходимо для конкретной задачи. Смысловая интер­претация классов, составляющих конкретный образ, является обя­зательным этапом серьезного исследования.

Случай (6.3) является наиболее общим. Он представляет собой ситуацию, когда окончательное решение задачи обработки данных возможно только при введении исследователем дополнительных све­дений или, что не всегда принимается во внимание, корректировки своих субъективных представлений о сущности искомого резуль­татаA_i.. Именно этот вариант наиболее типичен для обработки экспериментальных данных и обосновывает необходимость введе­ния какой-либо формы диалогового режима.

Дадим графическую интерпретацию приведенных ситуаций. На рис. 6.3, а представлен случай (6.1). В приведенном примере m=l=4. Следовательно, A_i=S_k.

Более сложная ситуация (6.2) иллюстрируется рис. 6.3, б. В этом случае l=2,m=4. Следовательно, вниманию исследователя должны быть представлены следующие варианты:

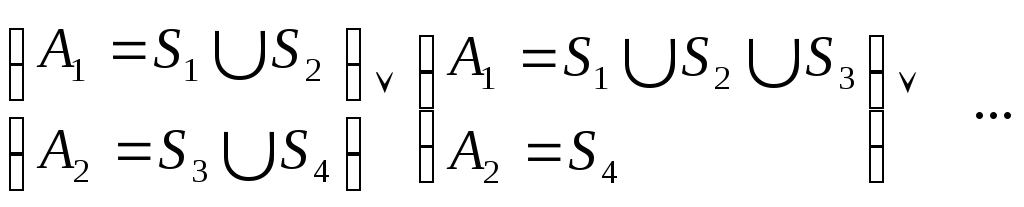т.д.

Случай (6.3) может быть интерпретирован следующим образом (рис. 6.3, в): математический аппарат Н и априорная информация исследователя А_iне согласованы между собой. Следовательно, надо либо изменить пространство описания П^p, либо искать другие решающие правила Н, либо исследовать физический смысл полученного группирования и внести коррективы в априорное пред­положение исследователя об образе А_i.

Отметим, что такое разнообразие альтернатив исследования яв­ляется в какой-то мере учетом поискового характера решений в ис­следовательском процессе, приводящего к необходимости поста­новки управляемого эксперимента. Грубейшей ошибкой следует считать восприятие как догмы результатов работы какого-либо алгоритма классификации без творческого осмысления специали­стом полученных результатов.

Выделение классов, т. е. объединение объектов Е в возможно более однородные группы, в общем случае состоит в определении семейства частей (подмножеств) S_kмножества Е, образующих по­крытие этого множества. Задача состоит в том, чтобы из всех возможных покрытий множества Е выбрать такое, которое окажется наиболее согласованным с информацией исследователя о допусти­мых разбиенияха_i.

Разобьем множество Е из N элементов на т подмножествS₁, … ,S_mтак, что

Рассматривая выбор из возможных разбиений как комбина­торную задачу, отметим, что задание образов А_iили правил Н можно интерпретировать как сужение комбинаторного перебора.

Итак, если возникает задача: сколько элементов, принадлежа­щих конечному множеству, обладает некоторым свойством или неко­торой совокупностью свойств, то это задача пересчета. Если же при этом требуется список элементов, обладающих этим свойством (или свойствами), то приходим к задаче перечисления. Однако при большом числе элементов (объектов) множества Е решение задачи перечисления прямым комбинаторным методом приводит к боль­шому объему вычислений. Поэтому-то на практике так часто и ре­шают задачу структуризации. В этом случае вместо соответствую­щего перечисления отдельных объектов выделяются подмножества S_kи правила вхождения элементов (объектов) множества Е в S_kс помощью какого-либо соотношения (критерия Н).

Интерпретация структуризации как экономного описания экспе­риментальных данных позволяет ввести ограничение сверху, т. е. исключить из рассмотрения слишком «мелкие» разбиения. При этом появляется возможность априорного ограничения числа подмно­жеств, или, иными словами, выделения максимального числа по­крытий множества Е, внутри которого возможен комбинаторный выбор.

Практически приходим к оптимизационной задаче — нахож­дению минимального числа т классов S_kмножества Е при условии максимальной «плотности»S_k. Под плотностью S_kпонимается отно­шение числа объектов, принадлежащих выделенному подмножеству, к объему, который оно занимает в пространстве описания:

(6.4)

Тогда задача выявления СД может быть представлена как вы­бор таких разбиений {P_*} множества Е, при котором получаем ми­нимальное число классов максимальной плотности_k. Свяжем с каждым допустимым разбиениемP_iвеличину средней плотности

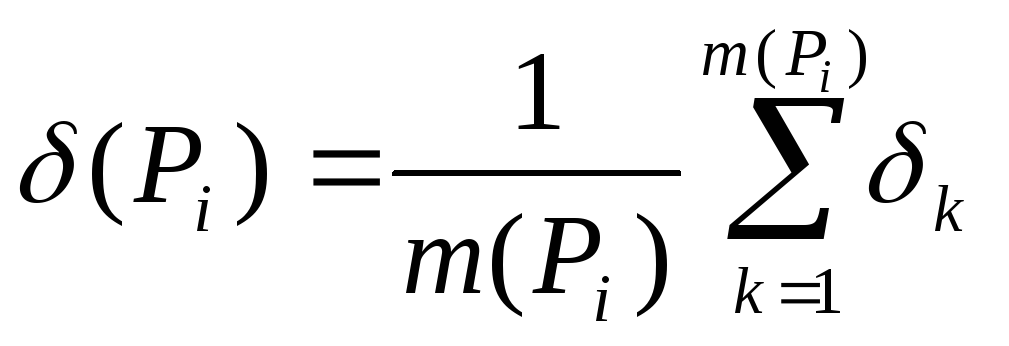
В этом случае разбиения {P_*} можно искать, например, как одновременно удовлетворяющие условиям:

(6.5)

(6.6)

Выражения (6.5), (6.6) позволяют еще более сузить перебор. Описанный комбинаторный принцип структуризации дает возможность проводить сопоставительный анализ между отдель­ными объектами, составляющими образыA_i, и классы S_k, что явля­ется необходимым условием организации диалогового режима при создании интерактивной системы обработки данных. Теоретико-множественный подход к решению задач структуризации и упоря­дочения объектов, использующий в своей основе принципы ком­бинаторной геометрии, позволяет ввести и использовать в качестве критерия упорядочения S_kвеличину условной «плотности»_k. Отсюда следует теоретико-множественная интерпретация задачи упорядочения и классификации как взаимно однозначного отобра­жения множества объектов исследования Е во множество допусти­мых решений V, которое определяется в пространстве R¹. Такое определение дает возможность визуального восприятия объектов Е, заданных в многомерном пространстве описания, т. е. ЕVR¹.

Следует заметить, что в любых схемах принятия решения всегда имеет место сведение многокритериального (многопараметриче­ского) описания задачи к однопараметрическому, так как про­странство R¹ — числовая шкала — обладает естественным и одно­значным отношением порядка.

По сути дела, вся проблема заключается в том, по какой мате­матической схеме реализуется подобная редукция. Так, например, в задачах распознавания образов байесовское решающее правило для определения принадлежности вектора х⁽¹⁾, ..., х^(p)к одному из двух образов А₁, А₂описывается выражением:

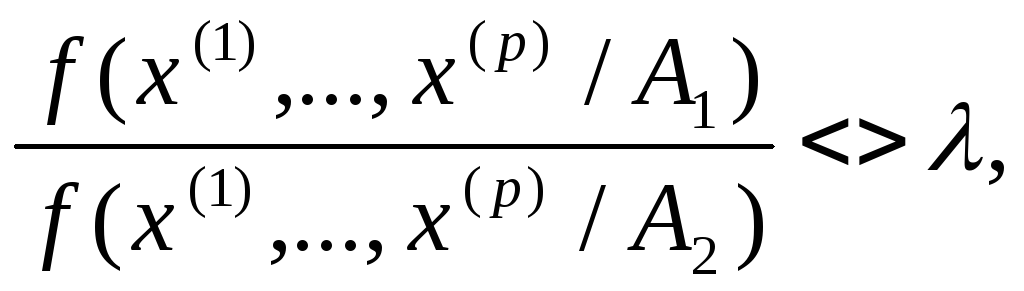
гдеf(•) — условная функция плотности распределения образа;R¹— пороговое значение, равное отношению априорных ве­роятностей появления объектов образовA₂и А₁, т. е. окончательное решение принимается в одномерном пространстве.

На рис. 6.4, а изображен случай распознавания образов, т. е. некоторый результат отображения ЕVR¹, когда все объектыA₁отображаются, к примеру, в левую часть, а все прочие — в правую. На рис. 6.4, б рассматривается случай автоматической классификации, когда решение о группировании принимается по какому-либо критерию, так или иначе связанному с оценкой критерия «плотности»и установления порога отсечки₀. Именно необходимость выбора значения порога отсечки₀или₀^’и опре­деляет возможную неоднозначность решения задачи классифика­ции. Приведенная на рис. 6.4, а, б условная интерпретация задач распознавания и классификации показывает роль субъективной классификации, задаваемой «учителем» в виде зон принятия ре­шения на R¹, а выбор порога₀— роль. На рис. 6.4, в показана условная интерпретация задачи функ­ционального упорядочения, возникающей, например, при опти­мизации на равномерной сетке вП^р. здесь=F ((х⁽¹⁾, . . ., х^(p)), где F — оптимизируемая функция;: П^pR¹ — функция отоб­ражения.

формального математического критерия.

Приведенная выше интерпретация позволяет анализировать с единых позиций различные математические схемы обработки данных, исследуя свойства подобных отображений и ограничения их применения.