Производные и ее основные свойства

Определение Пусть существует f определенная на (a,b), пусть x₀(a,b), тогда говорят, что функция f имеет производную в точке x₀, если существует (1)

Говорят, что функция дифференцируема в точке х₀ , если существует такая постоянная величина А и некая (h) при h0, для которых справедливо свойство:

f(x₀+h)-f(x₀)=Ah+(h) (2) и (3)

Теорема: Функция f имеет производную в точке х₀, тогда и только тогда, когда она дифференцируема в точке х₀. При это для значения f `(x<sub>0</sub>) и для числа А справедливо равенство А= f `(x₀)

Замечание: Из определения производной функции в силу свойства единственности предела, следует, что если существует производная в точке х₀, то она единственна. Определение не гарантирует, что существует единственное А.

Применение этой теоремы влечет единственность А

Доказательство: теоремы

Пусть существует производная

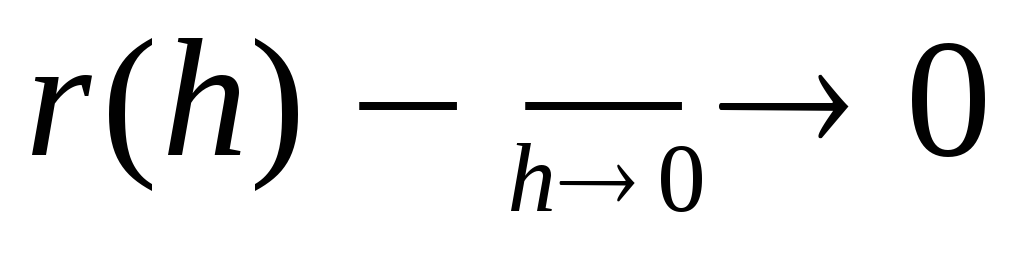1. => (5)

2. <=> f(x₀+h)-f(x₀)= f `(x₀)+hr(h)

A=f `(x₀)

(5)=>(3)

Пусть функция дифференцируема

=>f `(x₀)=A

Арифметические свойства функции, имеющей производную

1. f определена на (a,b), x₀(a,b), тогда f непрерывна на (а,b)

Доказательство:

f(x₀+h)-f(x₀)=Аh+(h) <=> f(x₀+h)=f(x₀)+Аh+(h)

f(x₀) = f(x₀) +0 + 0 (h0)

Значит f непрерывна на (а,b)

2. Пусть существует f `(x₀), C, тогда

(Cf)`(x<sub>0</sub>)=C f `(x₀)

Доказательство:

по свойствам предела

3. Пусть существует f `(x<sub>0</sub>), g `(x₀), тогда (f­+g)`(x<sub>0</sub>)=f `(x₀)+g `(x₀)

Доказательство:

4. Пусть существует f `(x<sub>0</sub>), g `(x₀), тогда (fg)`(x<sub>0</sub>)=f `(x₀) g(x₀)+g `(x₀) f(x₀)

Доказательство:

= f `(x<sub>0</sub>) g(x<sub>0</sub>)+g `(x₀) f(x₀)

5. Пусть существует g `(x₀) : g(x₀)0 x(a,b), тогда

Доказательство:

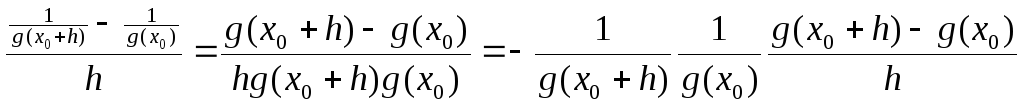
6. Пусть существует f `(x<sub>0</sub>), g `(x₀) : g(x₀)0 x(a,b), тогда

Доказательство:

7. Производная сложной функции

f определена на (a,b) : p<f(x)<q x(a,b) и существует g(y) определенная на (p,q), тогда y₀=f(x₀) существует g`(y₀)

(x₀)=g(f(x₀))

`(x<sub>0</sub>)=g`(y₀)f `(x₀)

Доказательство:

По определению и равенства (8)

(8)=>H=f(x₀+h)-f(x₀)=f `(x₀)h+₂(h) (9)

=> g`(y<sub>0</sub>) (f `(x₀)h+₂(h))+₁(f `(x₀)h+₂(h)

?????????????????

8. Производная обратной функции.

Пусть f определена, непрерывна и строго монотонна на [a,b]

Пусть x₀(a,b)

Пусть f дифференцируема в точке x₀, существует f `(x₀)0

g(y) – обратная функция, у₀=f(x₀)

Тогда g дифференцируема в точке y₀ и g`(y<sub>0</sub>)=1/f `(x₀)

Доказательство:

f(x₀+h)-f(x₀)=f `(x₀)h+(h)

f(x₀+h)=y₀+l

g(f(x₀+h))=g(y₀+l), x₀+h=g(y₀+l)

f(x₀)= у₀

g(f(x₀))=g(y₀)

x₀= g(y₀)

h= g(y₀+l)-g(y₀)

y₀+l-y₀=f `(x₀)(g(y₀+l)-g(y₀))+(g(y₀+l)-g(y₀))

(1)=> g(y₀+l)-g(y₀)=1/ f `(x<sub>0</sub>)<sup>.</sup>l +((-1/ f `(x₀))(g(y₀+l)-g(y₀)))

₁(l)= (1/ f `(x₀))(g(y₀+l)-g(y₀))

g(y₀+l)-g(y₀)=(1/ f `(x₀))₁(l)

Таблица основных производных

1) С`=0 Доказательство:

2) x`=1 Доказательство:

2`) (ax+b)`=1 Доказательство: (ax+b)`=ax`+b`=a

3) (x²)`=(x x)`=x` x+x x`=2x

(xⁿ)`=nx^n-1 ; xⁿ⁺¹=xⁿ x

3`)x0 (x<sup>-n</sup>)`=1/xⁿ= -nx^-n-1

4) (e^x)`= e^x Доказательство:

4`) (e<sup>Cx</sup>)`= C e^Cx Доказательство: (e^Cx)`= (e<sup>y</sup> )` (Cx)` (y=Cx)

5) (ln x)`=1/x , x>0 Доказательство:

y=ln x <=> x=e^y

(ln x)`=1/e^y=1/x (Обратная функция)

6. r0 rR, x>0 (x^r)`=r x^r-1 Доказательство:

(r ln x)`=r (ln x)`=r/x

(x^r)=(e^{r ln x})`= (e^{r ln x})(r/x)= r x^r-1

7. (Sin x)`=Cos x

(Cos x)`=-Sin x

Доказательство:

Пусть x=0,

Sin x= Sin (x-x₀+x₀)=Sin x₀ Cos(x-x₀)+ Cos x₀ Sin(x-x₀)

Cos x=Cos(x-x₀+x₀)=Cos x₀ Cos(x-x₀)-Sin x₀ Sin(x-x₀)

(Sin x)`=Sin x<sub>0</sub>(Cos(y))`(x-x₀)`+ Cos x<sub>0</sub>(Sin(y))`(x-x₀)`= Sin x₀ 1 0+Cos x₀ 1 1= =Cos x₀ (x=x₀)

Cos x аналогично

8. (tg x)`=1/cos²x

(ctg x)`=-1/sin²x

(tg x)`=

9. (arcsin(x))`=

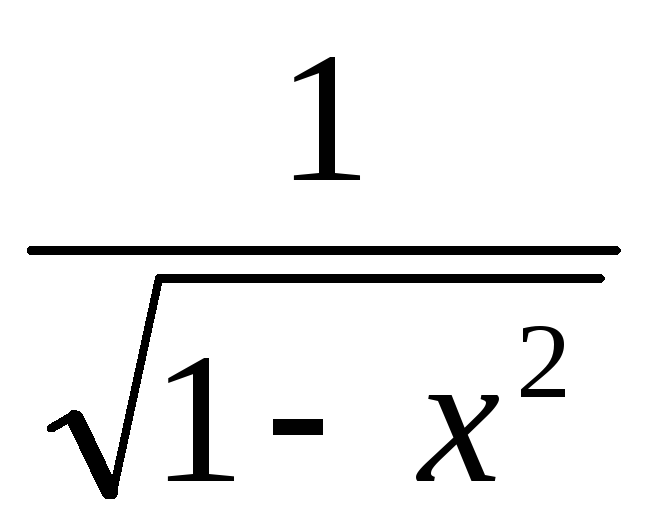
(arccos(x))`=

Доказательство:

y=arcsin(x), x=sin(y) -/2<y</2

(arcsin(x))`=1/(sin(y))`=1/cos(y)=

10) (arctg(x))`=

(arcctg(x))`=–

y=arctg(y), x=tg(y) -/2<y</2

(arctg(x))`=1/(tg(y))`=cos²(y)

x=tg y => x²+1= tg²y+1= sin²(y)/cos²(y)+1=1/cos²(y)