2. Структурная схема системы.

Структурная схема ЭСС, разработанная на основе ее функциональной схемы представлена на рис 2.

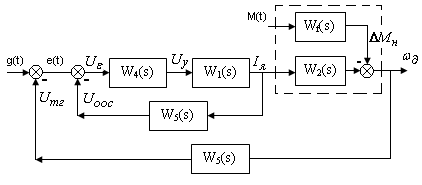
Рис. 2. Структурная схема ЭСС.

Причем:

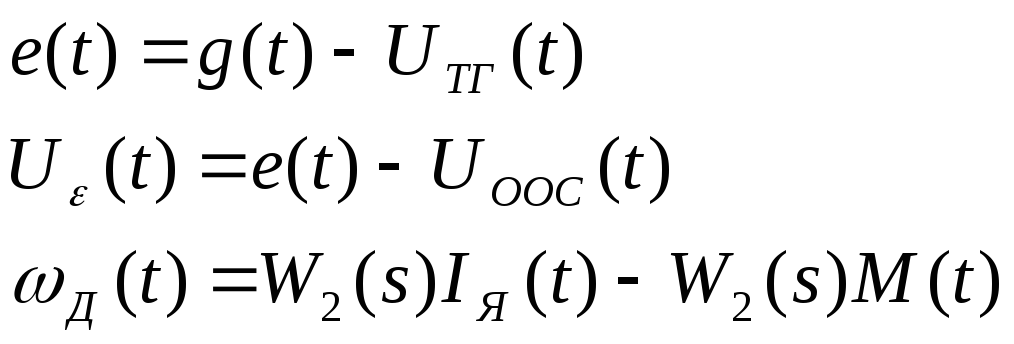
Знак “-” в последней формуле отражает уменьшение скорости при увеличении возмущающего воздействия на исполнительном валу двигателя

Соответствующие передаточные функции, с учетом произвольного выбора параметров из заданных интервалов, сведены в табл. 1.

Элементы ЭСС	Передаточные функции	Размерность
ЭМУ
УПТ		б/р
ИД по управлению
ИД по возмущению
ТГ
КУ		Ом

Параметры подлежат расчету на основе требований предъявляемых к системе.

3. Требования, предъявляемые к эсс.

Проектируемая следящая система создается для работы при скоростях и максимальном возмущающем воздействии.

Требования, предъявляемые к системе классифицированы по категориям, и сведены в табл. 2.

Требования	Параметр	Величина
Статические	Статическая ошибка стабилизации системы от задающего воздействия (на максимальных оборотах),
	Статическая ошибка стабилизации системы от возмущающего воздействия,
	Суммарная статическая ошибка стабилизации системы (на максимальных оборотах),
Динамические	Перерегулирование,
	Время регулирования,	< 0.3сек.
Частотные	Запас по амплитуде,
	Запас по фазе,
Чувствительность	Сохранение статических и динамических характеристик при изменении параметров

4. Анализ исходной системы.

4.1 Определение общего вида передаточных функций системы.

Исходя из составленной выше структурной схемы ЭСС (рис. 2.), определим общий вид передаточных функций, системы и ее ошибки.

Для регулируемой величины y(t) и ошибкиe(t) можно записать:

где - передаточная функция внутреннего контура системы.

Решая совместно два этих уравнения, получаем для регулируемой величины y(t):

и для ошибки:

Также определим ПФ разомкнутого контура:

В представленных выше формулах размерность регулируемой величины- [рад/с], а ошибки:- [В].

Из полученного выражения для регулируемой величины выделим передаточные функции замкнутого контура системы:

а) по заданию,

б) по возмущению.

Соответственно для ошибки:

а) по заданию,

б) по возмущению.

4.2 Расчет статического режима.

Поскольку местная отрицательная обратная связь является гибкой (не оказывает влияния на работу системы в статическом режиме), это позволяет перейти к расчету коэффициента усиления УПТ, обеспечивающего заданный уровень статической ошибки. Найдем ее из полученного выше выражения:

Положим s= 0,

где 125.6 рад/с - максимально возможная скорость движения исполнительного вала двигателя, а- максимально возможный момент сил нагрузки.

Поскольку , окончательно получаем:

где К - коэффициент усиления разомкнутого контура,

Из этого соотношения следует, что для обеспечения статической ошибки, не хуже 5 об/мин, коэффициент усиления должен быть не менее 49.23 дБ. Выбрав суммарное усиление разомкнутого контура 50 дБ (316 раз), окончательно получим , при этом система будет обеспечивать в рабочем диапазоне следующие статические ошибки:

- по заданию -

- по возмущению -

- суммарная ошибка -