20.Властивості міри Лебега.

Лема1 (про вимірність доповнення). Якщо Е вимірна множина, і то множина E:= I/E також вимірна, і виконується рівність

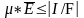Доведення: За означенням вимірної множини, та Оскільки I/F є відкритою, то За озн довжини замкненої множини, Тому .Оцінимо внутрішню міру. Позначимо . Тоді і замкнена множина. Використовуючи означення довжини замкненої множини, маємо = = Отже для будь-якого Внаслідок довільності - маємо

Тобто множина I/E вимірна і

Властивість(адетивність):Якщо множини Е₁ і Е₂ вимірні і Е₁ , то їх об’єднання є також вимірною множиною і

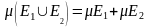
Властивість 4. Якщо множини Е₁ і Е₂ вимірні, то їх перетин є також вимірною множиною.

9.Множини потужності континуум та їх властивості.Потужність множини дійсни числ.

Теорема: Множина точок вдрізка [0,1] незчислена.

Множина точок [0,1] – зчистленна. Між точками відрізку [0,1] числової прямої та множини н.д.д., що мають цілу частину 0, окрім числа 1,000…, існує взаємооднозначна відповідність, тому будемо шукати потужність вказаної множини н.д.д., пам’ятаючи домовленість про відсутність в запису н.д.д. 9 в періоді. Тоді переіменуємо елементи вказаної множини:

Число b неспівпадає з жодним з чисел послідовності і не має 9 в періоді. Тобто це цисло виявилось не перенумерованим, що неможливо за припущенням. Отримано протиріччя.

ОЗН: Потужністю континуума або потужністю с називається потужність відрізку [0,1].

З означення випливає, що усі множини, що еквівалентні відрізку [0,1], мають потужність континуума.

Теорема2:Будь-який інтервал (a,b), відрізок [a,b] ,півінтервал [a,b) або (a,b] має потужність континуума.

Доведення:Оскільки [a,b]=с і відомо , що [0,1]~ [a,b], то [a,b]=с.Усі інші множини (ф вони є нескінченними) можна отримати відкиданням із відрізку скінченої кількості точок, наприклад,

Тому вони не змінюють потужність відрізка [a,b], залишаючись множинами потужності континуума.

Таким чином, відрізок [0,1] розробили на n півінтервалів, кожен з яких мае потужність с. Кожному з відповідних півінтервалівбієктивно співставляемо надвні множини:

Наслідок: Множина дійсних чисел має потужність с.

29. Рівність функцій майже всюди та інтеграл Лебега.

Теорема. Коли f(x) і обмежені вимірні функції на множині Е, , то

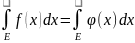
Позначивши

за попередньою теоремою ,

, з наслідку випливає . Для маємо і, отже, і .

Інтеграл Лебега визначають індуктивно, переходячи від більш простих функцій до складних. Будем вважати, що дано простір з мірою , і на ньому визначена вимірна функція .

Озн. Нехай — проста функція, де 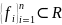, а — скінченне розбиття на вимірні множини. Тоді

.

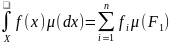Пр. Розглянемо функцію Діріхле 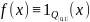, задану на , де — борелівська σ-алгебра на , а — міра Лебега. Ця функція принимає значення 1 в раціональних точках і 0 в ірраціональних. Легко побачити, що не інтегровна в сенсi Рімана. Однак, вона є простою функцією на просторі зі скінченною мірою, бо приймає тільки два значення, а тому її інтеграл Лебега визначений і дорівнює:

.