1.Взаємо-однозначна відповідність. Еквів. Множин.

Озн. Відображенням називається закон, за яким кожному елем. ставиться у відповідність єдиний ел. . Множина A називається множиною визначення відоб. f. .

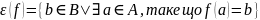Озн. Відображенням назив. ін’єкцією, якщо з умови

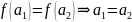
Озн. Відображенням назив. сюр’єкцією, якщо з умови .

Озн. Відображенням назив. бієкцією, якщо f ін’єкція і сюр’єкція.

Теорема. Якщо бієкція, то тоді визначено обернене відображення - бієкція.

Дов. .

1. f – обернене відображення?

, але f – ін’єкція, тому .

2. – ін’єкція?

Якщо , то тоді .

3. – сюр’єкція?

, а отже, – сюр’єкція. Доведено.

2. Потужність множин. Порівняння потужностей.

Озн. Говорять, множини 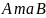мають однакову потужність(або та 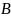еквівалентні), якщо 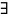відобр. , таке що 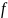– бієкція.

Відношення A~B еквівалентне, якщо

1. A~A

Потрібно побудувати . - буде бієкцією.

а) якщо то 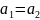і f – ін’єкція;

б) очевидно, що , тому – сюр’єкція, а отже, – бі’єкція

2. Із A~B випливає B~A

- бієкція, за теоремою про обернене відображення – бієкція, а отже B~A.

3. Із A~B і B~C випливає A~C

, покажемо, що знайдеться бієктивне відображення , тобто задається складене відображення g(f), що діє .

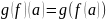а) Оскільки g- ін’єкція, то маємо 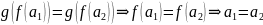, бо f – ін’єкція. Отже, g(f) – ін’єкція.

б) Доведемо, що . Для цього нехай дано елем. . Раз g – сюр’єкція, 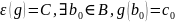. Раз f – сюр’єкція, то . Остаточно і . Доведено, що , отже, g(f) – сюрєкція, а отже, g(f) – бієкція. Тим самим всі множини розбиваються на класи еквівалентних множин.

Якщо маємо відображення і кількість елементів множини A – n, множини B – m, то з умови f – ін’єкція ви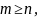пливає а з умови f – сюр’єкція випливає 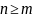, а так як f – бієкція, то , тобто еквівалентними будуть скінченні множини з однаковою кількістю елементів.

3. Теорема Кантора-Бернштейна.

Теорема. Якщо дві непорожні мн. A та B і - підмножина B, а – підмножина A, то тоді A~B.

Доведення.

Розглянемо взаємно-однозначну відповідність між , тоді підмножині буде відповідати підмножина 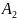, причому 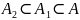, тобто 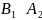. А так як і то за транзитивністю 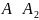. 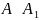, , отже, A~B. Доведено.

4. Поняття зчисленної множини. Найпростіші властивості.

Озн. Множина М назив зчисленною, якщо M~N, де N – множина натуральних чисел, тобто існую бієкція .

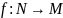Для зчисленною множини М існує бієкція , тобто і заповнюють усю множину M, тобто всі елементи M – перелічені (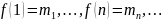 ), отже, можуть бути пронумеровані.

Властивості.

1. Будь-яка нескінченна множина X має зчисленну підмножину.

Нескінченність множини X означає, що існують елементи ,

Виділена підмножина еквівалентна N, тобто зчисленна.

2. Якщо A,B – зчисленні множини складені з різних елементів, то - зчисленна множина.

Проведемо нумерацію елементів по стовчиках, тобто спочатку пронумеруємо перші елементи множин, потім другі і так далі, остаточно всі елементи будуть пронумеровані, а отже, множина є зчисленною.

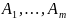3. Якщо - зчисленні множини складені з різних елементів, то тоді їх об’єднання є також зчисленна множина.

Доведення.

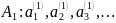
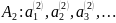
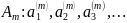
Проведемо нумерацію елементів по стовчиках, тобто спочатку пронумеруємо перші елементи множин, потім другі і так далі, остаточно всі елементи будуть пронумеровані, а отже, множина об’єднання даних множин є зчисленною.