25. Властивості вимірних функцій: вимірність суми, різниці, добутку та частки вимірних функцій.
1).
Якщо функції f(х), g(х) – вимірні на множині
А, то і сума (f(х) + g(х)) вимірна на множині
А. Доведення:
нехай дано число а, а є R, f(х), а-g(х)=а+(-1)
g(х) – вимірні. {х
є А/ f(х)
а g(х)}
– вимірна, {
х є А/ f(х) - g(х)
}
– вимірна для будь-яких а є R.
2). Якщо функції f(х), g(х) – вимірні на множині А, то і різниця (f(х) - g(х)) вимірна на множині А.
3).
Якщо f(х) – вимірна на множині А, то і
вимірна на множині А.
4)
Якщо функції f(х), g(х) – вимірні на множині
А, то і добуток
вимірний
на множині А. Доведення:
.
5).
Якщо f(х) – вимірна на множині А, і
то
і
вимірна на множині А.
6).
Якщо функції f(х), g(х) – вимірні на множині
А, і g(х)
вимірна
на множині А.
26. Інтеграл Рімана. Критерій інтегрованості функції за Ріманом.
26. Інтеграл Рімана. Критерій інтегрованості функції за Ріманом.
– інтеграл
Рімана – це границя інтегральних сум,
тобто
,
.
,
.
,
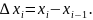
d
= max(
).
Теорема: для того, щоб
була інтегрована за Ріманом на [a,b]
необхідно і достатньо, щоб вона була
обмежена на [a,b],
міра множини її точок розриву дорівнювала
0. Властивості інтеграла Рімана: 1. Якщо
функції φ(х) та ψ(х) інтегровані по Ріману
на [a,b],
то
=
+
.
2. Якщо
інтегровна на [a,b]
і [b,с],
то вона інтегрована на [a,с],
при чому
=
+
.
3.
обмежена
інтегровна за Ріманом на [a,b],
то
.
27. Прості функції, інтеграл Лебега від простої функції.
Функція
називається
простою на множині А, якщо вона вимірна
на А та приймає не більше зчисленної
кількості значень. Твердження: функція
,
що на А приймає значення у1,
у2,…,
уn
… (попарно різні між собою), буде простою
тоді і тільки тоді, коли множина
вимірні за Лебегом. Якщо
проста функція на множині А, то
=
,
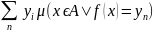якщо записаний ряд буде абсолютно
збіжним. Інтеграл Лебега від простих
функцій: 1.
=
,
якщо інтеграл існує і
проста. Доведення:
=
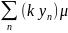{x
}
= k
{x
}
= k
.
2. Якщо
,
,
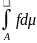то тоді
=
+
.
3. Обмежена проста функція
на
вимірній множині А інтегрована і за
умови, що
виконується рівність
.
.
28. Інтеграл Лебега, його найпростіші властивості
Озн.
Функція
називається сумовною на множині А, якщо
існує послідовність
простих
сумовних функцій, така що існує
=
,
при
і тоді інтегралом Лебега від функції
на множині А називається
=
Властивості: сумовна функція (не обов’язково проста).
1.
.
2.
=
Дов:
Нехай
рівномірно збігається до
,
при
,
,
тоді
=
=
=
=
.
3.
Адитивність.
,
,
то тоді
=
+
4. Обмежена
на вимірній множині А функція f(х)
інтегрована на множині А. 5. Якщо
на множині А і
,
то тоді
.
6. Якщо
та
,
,
то тоді
.
7. Якщо
множина А вимірна і на цій множині
нерівність
і
,
то має місце нерівність
Дов:
Маємо
.
=
=
.
8. якщо
,
то тоді
.
9.
та
існують або не існують одночасно.