31. Правило «северо-западного угла»

Груз распредел. с загрузки левой верхней, условно назыв-й северо-зап.,Если а₁>b₁, то х₁₁=b и первый потреб-ль В₁будет полностью удовл.В дальн первый столбец табл в расчет не приним, в нем перем x_i1=0(i= ). Двигаясь вправо по перв строке табл, заносим в кл-ку (1;2) меньш из чисел a₁ –b₁илиb₂, т.е. х₁₂=min(a₁ –b₁,b₂). Если a₁ –b₁<b₂, то х₁₂=a₁ –b₁и запасы перв пост-ка исчерп, перв строка табл в дальн в расчет не приним. Если а₁<b₁, то х₁₁=a₁и запас перв пост-ка будет исчерп. В дальн перв строка табл в расчет не приним, в нем перем x_1j=0(j=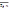 ). Двиг вниз по перв столбцу табл, заносим в кл-ку (2;1) меньш из чисел a₂,b₁–a₁, т.е. х₂₁=min(a₂,b₁–a₁). Если a₂>b₁-a₁, тох₂₁=b₁–a₁ перв потреб-ль будет полн удовл, перв столбец табл в дальн в расчет не приним. Далее аналог.

Процесс рапре-ия по 2й,3-й и последющим строкам(столбцам) произв-ся аналог распределению по 1й строке или 1му столбцу до тех пор,пока не исчерпаются рес-ы. Послед бужет заполнена кл-ка (m,n).

32.Прав «миним эл-та» (наим стоим»)

В распредел табл Просматр тарифы в распред-ной табл и в перв очередь заполн-ся клетка с миним знач тарифа. При этом в клетку запис-ся макс возмож знач поставки. Затем из рассмотрения исключ строку, соотв пост-ку, запасы которого полностью израсходованы, или столбец, соответствующий потребителю, спрос кот полн удовл. После этого из остав-ся клеток табл снова выбирают клетку с наим тарифом. Процесс распред закан-ся, когда все запасы пост-ков исчерп, а спрос потреб-ей полн удовл. В рез-те получ опорн план, кот должен содерж m+n-1 загруж.клеток.Но в процессе запол-ия табл м.б. однов-но искл. И строк и столбец.Так бывает когда полностью исчерпан запас груза и полностью удовлетворен спрос потребит. В этом случ в своб клетке,к-я не образ-т цикл с занятыми клет,надо зап-ть число 0 и усл-но считать такую кл-ку заня-й.

33. Теор о потенц. Алг теор

П лан ТЗ Х*=[x_ij]_mn явл. Оптим-м, если ему соотв-т система из m+n чисел Ui и Vj, кот. удовл-т след. Усл-м: 1) Ui+Vj*=Cij, x_j^*≥0; 2) ∆ij=cij-(Ui*+Vj*)≥0, X*ij=0 Расс-мТЗ: minF=Ʃ_i=1^mƩ_j=1ⁿc_ijx_ij–уравн1; Ʃ_j=1ⁿx_ij=a_i,i=1,m- уравн2; Ʃ_i=1^mx_ij=l_j,j=1,n–уравн3; x_ij≥0,i=1,m,j=1,n–уравн4. ТЗ 1-4 можно расм-ть как двойств.задачу к некот-й исходностизадачи,реш-ой на max. Построим задачу:Каждому i-му огранич-ю из 2 присвоим потенциалUi, а j-му огранич-ю из 3u_j.Тогда исход задача запиш в виде maxφ= + , Ui+Vj≤Ciji=1,m,j=1,nДля ТЗ оптим явл-ся план Х* а для исх. Задачи оптим явл план У*.На основ 1 теоремы двойств.задач имеет место правило: minF=maxF.А на основ 2-йтеор. Двойст.для оптим-ти планов пары двойствен задач вып-ся след усл:1)Ui*+Vj*=Cij, xij*>0; 2)Ui*+Vj*<Cij, xij*=0,На основ теор. след., что для ОП ТЗ необх. выполн-е усл-й: 1)кажд. занятой кл-ке в распред. табл. соотв. ∑ потенциалов, ровная тарифу этой клетки; 2)кажд. своб. кл-ке соотв-т ∑ потенц-в, не превыш-я тарифа этой кл-ке. Эк-кая оценка показ-т на сколько ден.ед. уменьш. трансп. издержки от загрузки данной кл-ки ед. груза. Алгоритм реш. ТЗ мет. потенциалов. 1)Проверить какого типа задача(откр.закр).В случае необход. Вводим фиктив.поставщика или потребит.2)Усл ТЗ запис-м в распред-ю табл.3) Строим нач-й опорный план по 1-му из правил.4)Опре-м потенциалы поставщ. Потребит-й: u_i+v_j=c_ijпо занятым клеткам.5) Опред-м оценки своб-х клеток ij.Если все они ≥0 то опорн-й план явл.оптим-м.Если все > то оптим. План явл.единст-м.6) если хотя бы 1 оценка < 0 то переходим с помощью цикла к др опорному плану.