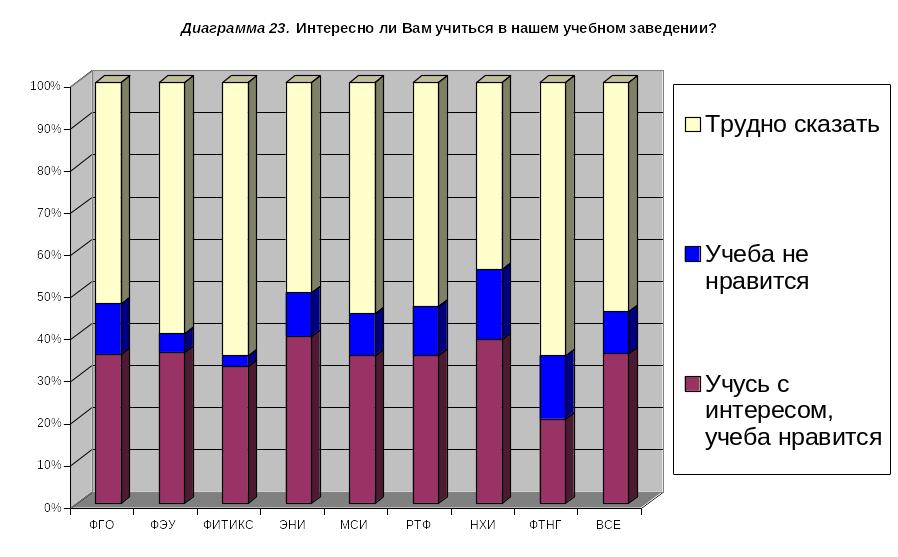
2. Двумерный анализ данных

Теперь мы мо­жем перейти к более сложному виду анализа, каким является двумерный анализ. Здесь рассматривается связь между двумя переменными. Мы имеем пары на­блюдений, полученные на одном объекте. Это могут быть, например, результаты по двум тестам. Нас инте­ресует, как один изучаемый признак связан с другим.

Таблица 3. Взаимосвязь между видом СМИ и характером суждений

Суждение	Вид СМИ		Всего
	Газета «Московский комсомолец»	Экспертный журнал
Рациональное (причины, анализ)	50 (19,6)	200 (81,6)	250
Оценочное (эмоционально-нравственное)	205 (80,4)	45 (18,4)	250
	255 (100)	245 (100)	500

В таблице 3 два столбца (для образования) и две строки, следовательно, размерность этой таблицы 2х2. Кроме того, имеются дополнительные крайний столбец и крайняя строка (маргиналы таблицы), указывающие общее количество наблюдений в данной строке или в столбце. В правом нижнем углу указана общая сумма, т. е. общее число наблюдений в выборке.

Обычно характер взаимоотношений между переменными в небольшой таблице можно определить даже «на глазок», сравнивая числа в столбцах или строках. Еще легче это сделать, если вместо абсолютных значений стоят проценты. Чтобы перевести абсолютные частоты, указанные в клетках таблицы, в проценты, нужно разделить их на маргинальные частоты и умножить на 100. Если делить на маргинал столбца, мы получим процент по столбцу.

Например, 50/255х100 = 19,6%, т. е. 19,6% газет МК имеют рациональные суждения. Если делить на маргинал строки, то мы получим другую величину - процент по строке.

Элементарная таблица сопряженности размерности 2х2 - это минимально необходимое условие для вывода о наличии взаимосвязи двух переменных.

3) Строится диаграмма распределения.

Между переменными могут существовать различные зависимости: линейные, нелинейные.

Между переменными Х и Y существует линейное отношение: если одна переменная возрастает по величине, то это же происходит и с другой. Очевидно, что чем более ком­пактно, «скученно» располагаются точки-наблюдения вокруг пунктирной пря­мой линии (описывающей идеальное линейное отношение Х и Y), тем сильнее зависимость. На рисунке 22 приведены три диаграммы рассеивания.

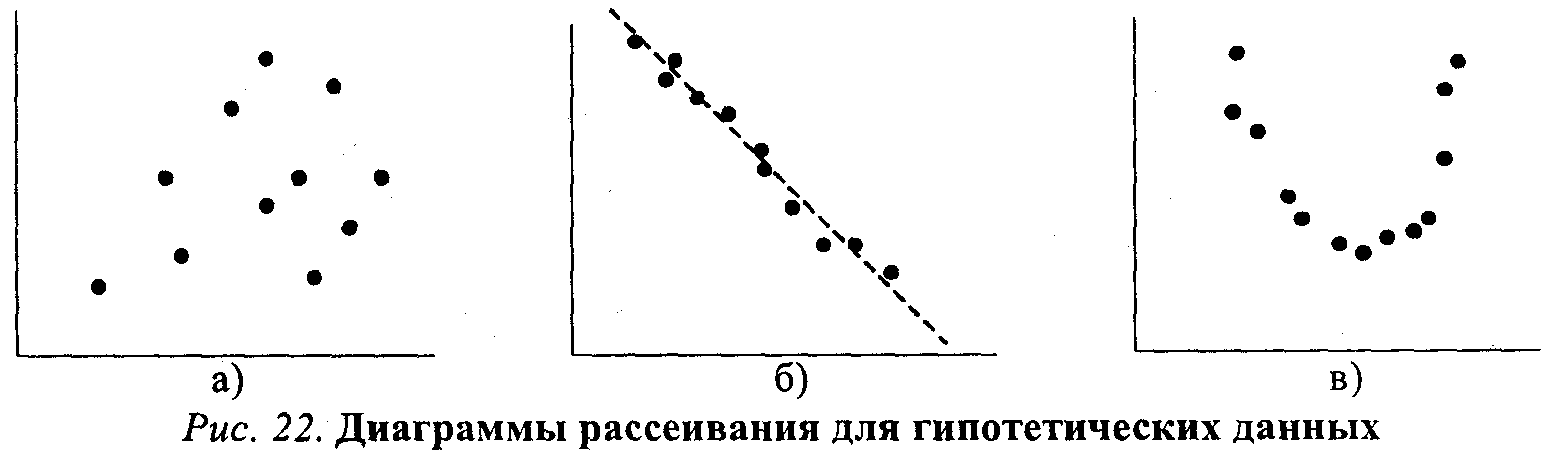
Очевидно, что на рисунке 22а какая-либо связь между x и y попросту отсут­ствует. На рисунке 22б воображаемая прямая линия (отмечена пунктиром) пе­ресекла бы диаграмму сверху вниз, из левого верхнего в правый нижний угол. Иными словами, линейная связь в этом случае имеет обратное направление: чем больше X, тем меньше зависимая переменная У.

Заметим также, что «куч­ность» расположения точек вдоль воображаемой прямой на рисунке 22б не очень велика, а значит и связь (корреляция) между переменными не только обратная, отрицательная, но еще и не очень сильная, умеренная.

Наконец, на рисунке 22в зависимую и независимую переменную связывает явно нелинейное отноше­ние: воображаемый график нисколько не похож на прямую линию и напомина­ет скорее параболу.

Методы анализа, о которых сейчас пойдет речь, не годятся для этого нелинейного случая, так как обычная формула для подсчета коэффициента корреляции даст нулевое значение, хотя связь между переменными существует.

Существует обобщенный показатель, позволяющий оценить, насколько связь между переменными приближается к линейному функциональному отношению, которое на диаграмме рассеивания выглядит как прямая линия. Это коэффици­ент корреляции, измеряющий тесноту связи между переменными, т. е. их тенденцию изменяться совместно.

Само слово «корреляция» как раз и озна­чает «взаимосвязь». Какого типа отношения возмож­ны между двумя переменными? Ну, во-первых, признаки могут быть совершенно независимыми друг от друга. Тогда изменения одного никак не связаны с из­менением другого. Мы говорим, что переменные не коррелированны между собой. Если признаки связаны, то сама связь может быть прямой или обратной.

В первом случае большим значениям одного признака соответствуют более высокие значения другого и на­оборот.

Во втором случае увеличение первого призна­ка сопровождается уменьшением второго, а уменьше­ние первого — увеличением второго.

Статистики гово­рят о положительной и отрицательной корреляции. Наконец, степень связи тоже может варьироваться от максимума, когда значения одного признака позволя­ют уверенно предсказывать значения другого, до ее полного отсутствия. Коэффициент корреляции отра­жает всю гамму возможных отношений. Его значение может варьироваться от +1 до — 1. Положительные значения указывают на прямую связь между перемен­ными, отрицательные — на обратную. Нуль соответствует случаю отсутствия корреляции.

Пример. Предположим, что у многих людей измеряют рост и вес тела. Каждый человек описывается двумя пока­зателями, и в результате образуются два ряда измере­ний. Сравнивая между собой пары измерений, мы стремимся выявить характер связи между переменными. Между ростом и весом тела существует довольно высокая положительная корреляция. Это значит, что высокий человек, как правило, весит больше, чем человек меньшего роста. Связь эта не однозначная: вы­сокий человек может быть очень худым, а человек не­высокого роста может быть очень полным. Поэтому значение коэффициента корреляции в данном случае находится где-то между 0 и +1, видимо, чуть ближе к единице.

Коэффициент корреляции по-разному вычисляет­ся для измеренных показателей (рост, вес) и для ран­жированных данных (оценки, предпочтения). Но его окончательная форма и интерпретация остаются теми же. Если данные носят качественный характер (муж­чина — женщина, совершеннолетний — несовершен­нолетний, работающий — пенсионер), то вместо коэф­фициента корреляции применяются другие меры связи, основанные на сравнении частот. Для тех случаев, когда два ряда получены с помощью разных шкал, име­ются свои вычислительные процедуры. Но общая ло­гика анализа сохраняется.

Социальные науки чаще всего имеют дело с явле­ниями, которые отличаются множественной детерми­нацией и контекстуальным характером. Поэтому необходима осо­бая тщательность в интерпретации наблюдаемых фак­тов.