- •1.Основные понятия
- •2. Компьютерное исследование точности
- •3.Исследование датчиков псевдослучайных чисел
- •3.1 Генерация псевдослучайных чисел
- •3.1.1 Генерация равномерных чисел
- •3.1.2 Генерация случайных чисел,
- •3.2 Тестирование датчиков
- •3.2.1.Проверка на соответствие заданному закону
- •3.2.2. Проверка независимости и некоррелированности
- •3.3. Наиболее часто встречающиеся законы распределения
- •3.4. Контрольные вопросы
- •4. Оценка параметров распределения
- •4.1. Вычисление точечных оценок
- •4.2. Вычисление интервальных оценок
- •4.2.1.Интервальная оценка дисперсии
- •4.2.2.Интервальная оценка математического ожидания
- •4.3. Точность оценивания параметров
- •4.4.Контрольные вопросы
- •5.1. Проверка гипотезы о математическом ожидании
- •5.2. Проверка гипотезы о дисперсии нормально распределенной
- •5.3. Проверка гипотезы о параметре экспоненциального
- •5.4. Точность проверки
- •5.5. Контрольные вопросы
- •6. Проверка статистических гипотез по критериям значимости (согласия)
- •6.1. Критерий значимости (согласия)
- •6.2. Проверка гипотез о параметрах нормально распределенной случайной величины
- •6.4. Точность проверки гипотез по критериям значимости
- •6.5. Контрольные вопросы
- •7.1.2.Проверка гипотезы по критерию Вилкоксона
- •7.2. Проверка гипотезы о наличии статистической независимости
- •7.2.1 Коэффициент ранговой корреляции Спирмена
- •7.2.2. Коэффициент ранговой корреляции Кендалла
- •7.3. Исследование точности ранговых критериев
- •7.4. Контрольные вопросы

 московский
московский
АВИАЦИОННЫЙ ИНСТИТУТ
В.В. БОМАС
М.А. КРАСОВСКАЯ
КОМПЬЮТЕРНОЕ
ИССЛЕДОВАНИЕ
ТОЧНОСТИ
СТАТИСТИЧЕСКИХ
МЕТОДОВ
МОСКВА • 1998
Бомас В.В., Красовская М.А. Компьютерное исследование точности статистических методов: Учебное пособие. – М.: Изд-во МАИ, 1998ю-68 с.:ил.
Рассматриваются наиболее распространенные в статистической практике методы оценки параметров и проверки статистических гипотез. В отличие от традиционных пособий на эту же тему, делается упор на использовании методов в случаях малых выборок и оценку точности принимаемых решений на основе компьютерного моделирования.
Пособие ориентировано на студентов специальности « Автоматизированные системы обработки информации и управления» МАИ, выполняющих в процессе изучения курса «Теория вероятностей и математическая статистика» лабораторные и курсовые работы.
Рецензенты: А.Р. Федоров, Н.К.Бодунов
Предисловие
Современные вычислительные средства позволяют генерировать псевдослучайные числа, подчиненные произвольно выбранному, т.е.любому, распределению. При этом объем генерируемых выборок и их число находится во власти экспериментатора. Это создало возможность экспериментального исследования точности и корректности применения статистических методов, основанных на предельных распределениях и законах больших чисел, когда объем выборок невелик и упомянутые распределения, строго говоря, неприменимы.
В пособии рассматриваются задачи точечного и интервального оценивания и проверки статистических гипотез о параметрах и законах распределения случайных величин. Отличительной чертой изложения является акцентирование внимания на тех элементах процедур оценивания, которые опираются на большой объем выборок. При этом ставится задача оценки влияния невыполнения этого условия на точность решения и приводятся алгоритмы, ориентированные на исследования точности рассмотренных методов применительно к выборкам малого объема.
В методическом и терминологическом отношении данная работа опирается на учебную литературу [1,2 и4].
Практическое применение предлагаемых в пособии приемов исследования точности статистических процедур предполагается в рамках лабораторных работ по «Теории вероятностей и математической статистика» [6], которые легко адаптируются к указанным задачам.
Авторы пользуются случаем поблагодарить своих коллег и соавторов [6] Павленко А.И. и Зайцева А.В., чьи разработки были использованы при написании пособия.
1.Основные понятия
В математической статистике одним из фундаментальных является понятие генеральной совокупности. Под этим понимается множество всех возможных реализаций случайной величины, в которой частота повторений каждого значения равна его вероятности. Генеральная совокупность содержит исчерпывающую информацию о случайной величине. Однако генеральная совокупность практически нереализуема и является абстракцией, удобной для дальнейших рассуждений, так как её свойства – это свойства случайной величины.
Экспериментируя со случайной величиной, мы получаем в результате множество наблюдений, которое можно рассматривать как случайную выбранную часть генеральной совокупности. Поэтому экспериментальные данные в статистике принято называть выборочной совокупностью, или случайной выборкой, или просто выборкой. Число наблюдавшихся значений, т.е число опытов, обозначают как объем выборки. Таким образом, случайная выборка принципиально ограничена.
На основе введенных понятий задачу обработки наблюдений случайной величины можно сформулировать так: определить по случайной выборке свойства генеральной совокупности. Однако такая задача при ближайшем рассмотрении оказывается неразрешимой. Дело в том, что в силу случайности выборки она не обладает основным свойством генеральной совокупности: частоты наблюдавших значений не только не равны соответствующим вероятностям, но могут значительно от них отличаться. Причем в этом качестве каждая новая выборка будет отлична от предыдущих. Поэтому характеристики одной и той же случайной величины, находимые по разным выборкам, будут отличаться как друг от друга, так и от аналогичных характеристик генеральной совокупности. В математической статистике принято, в силу этого, говорить не об определении свойств генеральной совокупности, а лишь об их оценивании, понимая под этим поиск подходящих числовых значений по данным случайной выборки ограниченного объема.
Таким образом, по данным эксперимента находятся не распределения случайных величин и их параметры, а лишь оценки этих распределений и параметров. Можно сказать, что оценка некоторой характеристики случайной величины – это её значение, найденное экспериментальным путем (по случайной выборке). Выборки носят случайный характер, поэтому и оценки являются случайными. Они характеризуются, как и все случайные величины, с помощью законов распределения или же числовых характеристик. Это свойство оценок принципиально.
Еще одним фундаментальным понятием является статистика. Под статистикой понимается любая функция случайной выборки (результатов наблюдений). Например: среднее значение наблюдений, среднее значение квадрата или любой другой степени наблюдений и т.п. Чаще всего, по причинам, о которых будет сказано ниже, статистики формируются в виде сумм. Используя понятие статистики, оценку можно определить следующим образом: оценкой некоторой характеристики случайной величины называется статистика, которую мы приравниваем (полагаем равной) этой характеристике.
Например, оценкой математического ожидания обычно служит среднее арифметическое наблюдавшихся значений случайной величины.
Пусть мы производим n наблюдений дискретной случайной величины X. Обозначим случайную выборку объема n следующим образом:
![]() ,
,
где
![]() - порядковый номер наблюдения (опыта);
- порядковый номер наблюдения (опыта);
![]() - значение случайной величины в i-м
опыте; n – число наблюдений
(опытов).
- значение случайной величины в i-м
опыте; n – число наблюдений
(опытов).
Множество {xi}содержит повторяющиеся элементы и неупорядоченно по x. Последовательность x1, … , xn называют неупорядоченным статистическим рядом. Это, по существу, первичный протокол эксперимента.
Первоначальная обработка результатов
эксперимента заключается в упорядочении
множества {xi}и
создании нового множества {xj},
![]() (k ≤ n),
обладающего свойством
(k ≤ n),
обладающего свойством
![]() Оно состоит уже только из неповторяющихся
элементов и каждому из них ставится в
соответствие число его повторений в
эксперименте m j
или частота
Оно состоит уже только из неповторяющихся
элементов и каждому из них ставится в
соответствие число его повторений в
эксперименте m j
или частота
![]() Множество {xj}называют
вариационным рядом.
Множество {xj}называют
вариационным рядом.
Вариационный ряд удобно представить в виде следующей табл.1.
Таблица1
|
|
|
…… |
|
|
|
|
|
…… |
|
|
|
|
|
…… |
|
|
В табл.1
![]()
Выше было сказано, что X – дискретная величина. Это не нарушает общности, так как если X непрерывна, она в процессе измерений неизбежно квантуется с дискретной, равной точности измерений. Кроме того, в процессе создания вариационного ряда можно, если это удобно, разбить множество значений непрерывной X на интервалы, приписав каждому из них значения в одной из его точек ( например, в центре) и дискретизировать X таким образом.
На основе вариационного ряда можно
вычислить функцию
![]() ,
представляющую собой статистический
аналог функции распределения и называемую
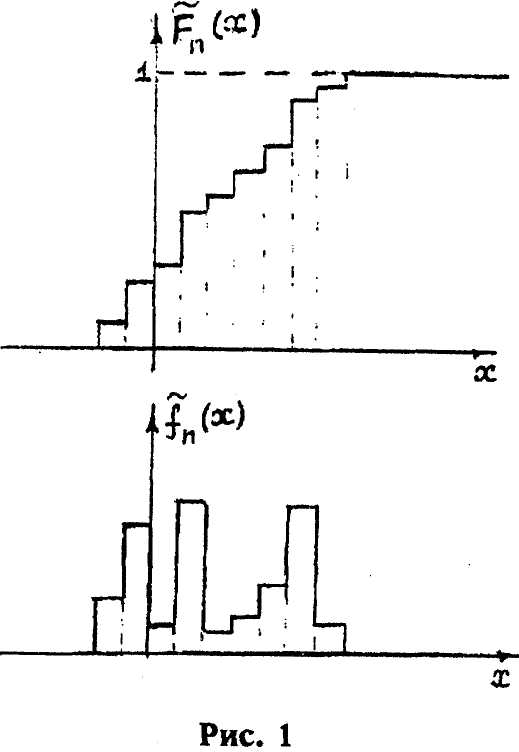
эмпирической функцией распределения.
,
представляющую собой статистический
аналог функции распределения и называемую
эмпирической функцией распределения.
Для непрерывной X, которая
приближена совокупностью k
интервалов длиной ∆, можно вычислить
ступенчатую функцию![]() где
где
![]() – частота, с которой X
принимает значение внутри j-го
интервала, а xj
– постоянное в пределах ∆ j
значения X. Функция
– частота, с которой X
принимает значение внутри j-го
интервала, а xj
– постоянное в пределах ∆ j
значения X. Функция
![]() является статистическим аналогом
плотности распределения и называется
гистограмма.
является статистическим аналогом
плотности распределения и называется
гистограмма.
На рис. 1 показаны эмпирическая функция и гистограмма распределения X.
В математической статистике различают две задачи, связанные с получением и обработкой наблюдений:
оценивание законов распределения и их параметров;
проверка гипотез о законах распределения и их параметрах.
Обе эти задачи решаются на основе случайных выборок. Первая состоит в том, чтобы по данным эксперимента найти наиболее подходящие к нему характеристики распределения случайной величины. Вторая заключается в том, чтобы оценить, насколько выдвинутая ранее гипотеза о распределении случайной величины согласуется с полученными экспериментальными данными.