Простейшие свойства линейного оператора

1º. Линейный оператор переводит нейтральный элемент пространства в нейтральный элемент пространства .

►Пусть – линейный оператор. Тогда .◄

2º. При линейном операторе линейно зависимые векторы пространства переходят в линейно зависимые векторы пространства .

►Пусть – линейно зависимые векторы. Это значит, что существуют числа 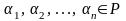, не все равные нулю, такие, что

. (4.7)

Подействуем линейным оператором на обе части равенства (4.7). Тогда

(4.7) [(4.3) и 1º]

.

Так как среди чисел есть отличные от нуля, то система { } линейно зависима.◄

Теорема 4.1. Пусть и – линейные пространства над одним и тем же полем P и пусть в пространстве задан базис

, (4.4)

а в пространстве – произвольная система векторов

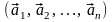. (4.5)

Тогда существует единственный линейный оператор , переводящий базис (4.4) в систему (4.5), то есть такой, что

: . (4.6)

►Построение. Выберем произвольный вектор и разложим его по базису (4.4): . Положим по определению

.

Линейность. Если – произвольные векторы, , то , , , . Тогда

= [определение f] = ;

.

Выполнение (4.6). Заметим, что все координаты вектора в базисе (4.3) равны нулю, за исключением k-й, которая равна 1. Таким образом, i-я координата вектора равна , то есть . Тогда

,

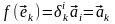значит, условие (4.6) выполнено.

Единственность. Предположим, что существует еще один линейный оператор , , переводящий (4.4) в (4.5), то есть такой, что . Тогда 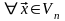: – противоречие.◄

17. Определение матрицы линейного оператора. Связь координат вектора с координатами его образа.

Пусть в линейном пространстве над полем задан базис

(4.8)

и пусть – линейный оператор (читается так: в себя). Построим систему векторов

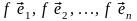( ). (4.9)

Каждый из векторов системы (4.9) можно разложить по базису (4.8):

(4.10)

Сокращенно система (4.10) записывается одним равенством:

. (4.11)

Расположим числа в матрицу А по нашей договоренности: верхний индекс обозначает номер строки, а нижний – номер столбца:

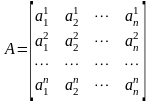
Заметим, что столбцы полученной матрицы А являются координатными столбцами образов векторов базиса (4.8) в том же базисе. Обозначим

[ ] = .

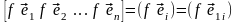Равенство (4.11) можно переписать и так: , откуда, руководствуясь правилом цепочки, (4.11) записываем в матричном виде:

. (4.12)

Матрицей линейного оператора в некотором базисе называется матрица А, столбцами которой являются координатные столбцы образов базисных векторов в том же базисе. Это матрица , элементы которой удовлетворяют системе равенств (4.10) или (4.11), а сама матрица удовлетворяет матричному равенству (4.12).