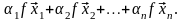- •Определение линейного пространства и простейшие следствия из аксиом.
- •2.Определение линейной зависимости и независимости элементов линейного пространства. Свойства линейной зависимости и независимости.
- •3.Базис и координаты в линейном пространстве. Свойства координат векторов.
- •Свойства координат векторов
- •4.Матричный критерий линейной зависимости и независимости.
- •5.Определение размерности линейного пространства. Теорема о связи базиса и размерности. Следствия.
- •6.Определение аффинного пространства и следствия из аксиом.
- •Как пример аффинного, евклидова и метрического пространств.
- •Свойства расстояния
- •Подпространства линейного пространства.
- •Линейные оболочки. Теорема о размерности линейной оболочки произвольной системы векторов.
- •10.Теорема о размерности линейной оболочки строк (столбцов) матрицы.
- •11. Сумма и пересечение подпространств линейного пространства. Теорема о сумме и пересечении подпространств.
- •Свойства матрицы перехода
- •14. Определение матрицы перехода. Изменение координат вектора при изменении базиса. Изменение координат вектора при изменении базиса
- •15. Понятие отображения. Произведение (композиция) отображений. Ассоциативность произведения. Тождественное отображение и его свойства. Взаимно однозначное отображение. Обратное отображение.
- •16. Определение линейного оператора и его простейшие свойства. Теорема о существовании линейного оператора.
- •Простейшие свойства линейного оператора
- •17. Определение матрицы линейного оператора. Связь координат вектора с координатами его образа.
- •Связь координат вектора с координатами его образа
- •18. Изменение матрицы линейного оператора при изменении базиса. Подобные матрицы. Изменение матрицы линейного оператора при изменении базиса
- •19. Операции над линейными операторами.
- •20. Невырожденные линейные операторы. Теорема о матрице.
- •21.Невырожденные линейные операторы. Теорема о взаимной однозначности.
- •22.Обратный линейный оператор.
- •23.Определение и свойства изоморфизма линейных пространств.
- •Свойства изоморфизма
- •24. Определение изоморфизма линейных пространств. Теорема о размерности изоморфных пространств.
- •25.Определение изоморфизма линейных пространств. Теорема об изоморфизме пространств одинаковой размерности.
- •26.Линейные формы.
- •27. Определение и свойства собственных векторов.
- •Свойства собственных векторов
- •30. Лемма о размерности пространства собственных векторов с одинаковыми собственными значениями.
- •31. Определение приводимости квадратной матрицы к диагональному виду и вторая теорема о приводимости.
- •32. Присоединенные векторы и правило их нахождения.
- •Правило нахождения присоединенных векторов
15. Понятие отображения. Произведение (композиция) отображений. Ассоциативность произведения. Тождественное отображение и его свойства. Взаимно однозначное отображение. Обратное отображение.
Пусть
Х
и Y
– множества элементов произвольной
природы. Говорят, что задано отображение
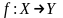 (читается:
отображение
f
множества X
во множество Y),
если задан закон, по которому каждому
элементу
(читается:
отображение
f
множества X
во множество Y),
если задан закон, по которому каждому
элементу
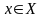 ставится в соответствие вполне
определенный элемент
ставится в соответствие вполне
определенный элемент
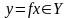 (рис. 4.1).
(рис. 4.1).

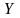

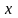
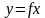

Рис. 4.1
Если
,
то
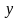 называется образом
элемента
;
– прообразом
элемента
при отображении f.
называется образом
элемента
;
– прообразом
элемента
при отображении f.
Примерами
отображений являются функции, которые
изучаются в школьном курсе математики
и в математическом анализе, например,
функция
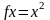 – отображение
– отображение
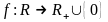 .
Классный журнал является примером
отображения множества учеников в классе
во множество всех фамилий.
.
Классный журнал является примером
отображения множества учеников в классе
во множество всех фамилий.
Отображение
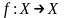 называется тождественным,
если оно любой элемент оставляет на
месте. Тождественное отображение
множества X
на себя будем обозначать
называется тождественным,
если оно любой элемент оставляет на
месте. Тождественное отображение
множества X
на себя будем обозначать
 .
Таким образом,
.
Таким образом,
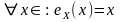 .
.
Отображение называется взаимно однозначным (или биективным, или биекцией), если оно удовлетворяет двум условиям:
1.
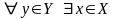 такой, что
такой, что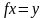 .
.
2.
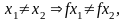
или одному, эквивалентному им, третьему условию:
3.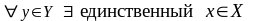 такой,
что
такой,
что
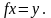
Хороший пример взаимно однозначного отображения: в театре дают билет, каждому билету соответствует некоторое кресло, причем только одно.
Отображения
и
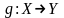 называются равными,
если
называются равными,
если
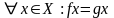 .
.
Пусть
заданы отображения
и
 .
Произведением
(или
композицией) отображений f
и g
называется отображение
.
Произведением
(или
композицией) отображений f
и g
называется отображение
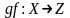 такое, что
такое, что
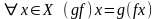 (рис. 4.2).
(рис. 4.2).

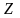
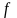


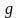
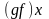
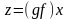
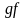
Рис. 4.2
Замечание. В произведении отображений сначала действует внутреннее, а затем внешнее отображение.
Примером произведения отображений является сложная функция.
Лемма
4.1.
Произведение отображений ассоциативно,
т. е. если заданы отображения
,
и
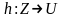 ,
то
,
то
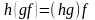 .
.
Для
доказательства равенства отображений
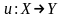 и
и
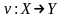 нужно показать, что
нужно показать, что
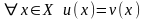 .
.
Итак, выберем произвольное . Тогда
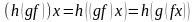 ;
(4.1)
;
(4.1)
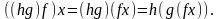 (4.2)
(4.2)
Сравнивая
(4.1) и (4.2), видим, что
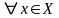 :
:
 и поэтому,
.
и поэтому,
.
Отображение
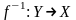 называется обратным
к отображению
,
если
называется обратным
к отображению
,
если
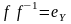 и
и
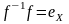 (рис. 4.3).
(рис. 4.3).
16. Определение линейного оператора и его простейшие свойства. Теорема о существовании линейного оператора.
Определение.
Пусть
и
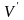 –
линейные пространства над одним и тем
же полем
–
линейные пространства над одним и тем
же полем
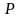 .
Отображение
.
Отображение
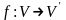 называется линейным
оператором,
если оно удовлетворяет следующим
условиям:
называется линейным
оператором,
если оно удовлетворяет следующим
условиям:
1*.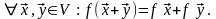
2*.
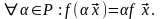
Следствие.
При линейном операторе образ линейной
комбинации векторов равен такой же
линейной комбинации их образов, т. е.
если
–
линейный оператор, то
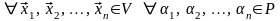 :
:
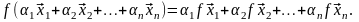 (4.3)
(4.3)
Доказательство проведем методом математической индукции по количеству векторов.
а)
n
=
1:
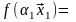 [2*]
[2*]
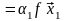 –
истинно.
–
истинно.
б) Предполагая, что утверждение верно для (n-1)-го вектора, доказываем его для n векторов.
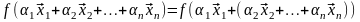 =
[1*] =
=
[1*] =
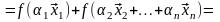 [2*
и предположение индукции] =
[2*
и предположение индукции] =
=