
- •Определение линейного пространства и простейшие следствия из аксиом.
- •2.Определение линейной зависимости и независимости элементов линейного пространства. Свойства линейной зависимости и независимости.
- •3.Базис и координаты в линейном пространстве. Свойства координат векторов.
- •Свойства координат векторов
- •4.Матричный критерий линейной зависимости и независимости.
- •5.Определение размерности линейного пространства. Теорема о связи базиса и размерности. Следствия.
- •6.Определение аффинного пространства и следствия из аксиом.
- •Как пример аффинного, евклидова и метрического пространств.
- •Свойства расстояния
- •Подпространства линейного пространства.
- •Линейные оболочки. Теорема о размерности линейной оболочки произвольной системы векторов.
- •10.Теорема о размерности линейной оболочки строк (столбцов) матрицы.
- •11. Сумма и пересечение подпространств линейного пространства. Теорема о сумме и пересечении подпространств.
- •Свойства матрицы перехода
- •14. Определение матрицы перехода. Изменение координат вектора при изменении базиса. Изменение координат вектора при изменении базиса
- •15. Понятие отображения. Произведение (композиция) отображений. Ассоциативность произведения. Тождественное отображение и его свойства. Взаимно однозначное отображение. Обратное отображение.
- •16. Определение линейного оператора и его простейшие свойства. Теорема о существовании линейного оператора.
- •Простейшие свойства линейного оператора
- •17. Определение матрицы линейного оператора. Связь координат вектора с координатами его образа.
- •Связь координат вектора с координатами его образа
- •18. Изменение матрицы линейного оператора при изменении базиса. Подобные матрицы. Изменение матрицы линейного оператора при изменении базиса
- •19. Операции над линейными операторами.
- •20. Невырожденные линейные операторы. Теорема о матрице.
- •21.Невырожденные линейные операторы. Теорема о взаимной однозначности.
- •22.Обратный линейный оператор.
- •23.Определение и свойства изоморфизма линейных пространств.
- •Свойства изоморфизма
- •24. Определение изоморфизма линейных пространств. Теорема о размерности изоморфных пространств.
- •25.Определение изоморфизма линейных пространств. Теорема об изоморфизме пространств одинаковой размерности.
- •26.Линейные формы.
- •27. Определение и свойства собственных векторов.
- •Свойства собственных векторов
- •30. Лемма о размерности пространства собственных векторов с одинаковыми собственными значениями.
- •31. Определение приводимости квадратной матрицы к диагональному виду и вторая теорема о приводимости.
- •32. Присоединенные векторы и правило их нахождения.
- •Правило нахождения присоединенных векторов
5.Определение размерности линейного пространства. Теорема о связи базиса и размерности. Следствия.
Определение. Число n
называется размерностью линейного
пространства V, а
само пространство V
называется n-мерным,
если в V существует
линейно независимая система из n
векторов, а любая система из (n
+ 1)-го вектора линейно зависима.
Размерность пространства
 по определению считается равной нулю.
по определению считается равной нулю.
Следствие. В n-мерном пространстве любая система из m векторов при m > n линейно зависима.
Следствие. Любой базис конечномерного линейного пространства V содержит одинаковое количество векторов.
Теорема 3.2. Для того чтобы линейное пространство было n-мерным, необходимо и достаточно, чтобы в нем существовал базис, состоящий из n векторов.
► Достаточность. Дано: в пространстве V существует базис из n векторов
( ). (3.27)
Тогда в V есть линейно независимая система из n векторов (это система (3.27)). Покажем, что любая система из (n + 1)-го вектора в этом пространстве линейно зависима. Выберем одну из них:
( ).
(3.28)
).
(3.28)
Каждый
вектор системы (3.28) можно разложить по
базису (3.27). Обозначим
 – координатные столбцы векторов системы
(2) в базисе (1). Тогда
– координатные столбцы векторов системы
(2) в базисе (1). Тогда

(так
как эта матрица имеет только n
строк). По матричному критерию система
(3.28) линейно зависима и, таким образом,
 .
.
Необходимость.
Дано:
 .
Согласно определению, в пространстве
.
Согласно определению, в пространстве
 существует линейно независимая система
из
существует линейно независимая система
из
 элементов. Пусть
элементов. Пусть
( ) – (3.29)
одна
из таких систем. Но
 система
система
( )
(3.30)
)
(3.30)
линейно зависима. По 4-му свойству линейной зависимости (§ 2) вектор
можно представить в виде линейной комбинации векторов системы (3.29), т. е.

Таким образом, (3.29) – система образующих пространства V, а значит, и его базис. ◄
6.Определение аффинного пространства и следствия из аксиом.
Пусть
А
–
множество элементов произвольной
природы, V
– действительное линейное пространство.
А
называется
аффинным
пространством,
связанным с линейным пространством V,
если задан закон, по которому каждой
паре элементов
 ,
где
,
где
 ,
ставится в соответствие элемент
,
ставится в соответствие элемент
 ,
причем выполняются две аксиомы.
,
причем выполняются две аксиомы.
1*. (рис. 3.1).
(рис. 3.1).
2*.
 единственный
такой, что
единственный
такой, что
 .
Этот вектор обозначается
.
Этот вектор обозначается
 .
.
1°.

► :
:
 .
С другой стороны,
.
С другой стороны,

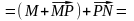 [1*] =
[1*] =
 На основании второй аксиомы получаем
требуемое.◄
На основании второй аксиомы получаем
требуемое.◄
2°.

►Если
 содержит одну точку, то утверждение
очевидно. Если же не одну, то
содержит одну точку, то утверждение
очевидно. Если же не одну, то
 ◄
◄
3°.


 Но
и
Но
и
 .
Поэтому на основании второй аксиомы
получаем
.
Поэтому на основании второй аксиомы
получаем
 ,
что равносильно доказываемому утверждению.
◄
,
что равносильно доказываемому утверждению.
◄
Как пример аффинного, евклидова и метрического пространств.
Важнейшим примером аффинного пространства является пространство . Положим
 ,
,
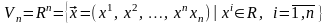 .
.
Для
любых
 и
и
 определим операцию
определим операцию
 .
Проверим выполнение аксиом:
.
Проверим выполнение аксиом:







 ;
;
 положим
положим
 .
.
Тогда

Предположим,
что существует вектор
 такой, что
.
Пусть
такой, что
.
Пусть
 .
Значит,
.
Так как
,
то
.
Значит,
.
Так как
,
то
 и поэтому
и поэтому
 .
Следовательно,
.
Следовательно,
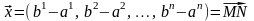 –
противоречие.
–
противоречие.
Таким образом, пространство с введенной в нем операцией откладывания вектора от точки становится n-мерным аффинным или точечным пространством.
.
Скалярным
произведением
векторов
и
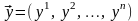 пространства
назовем число
пространства
назовем число
 .
.
Свойства скалярного произведения
1.

2.

3.

4.
 причем
причем

Свойства 1 – 4 вы легко докажете в качестве упражнения исходя из определения скалярного произведения в .
Пространство с введенной в нем операцией скалярного произведения называется евклидовым пространством (подробно категорию евклидовых пространств мы будем изучать в шестой главе).
Из
свойства 4
скалярного
произведения видно,
что
для любого вектора
 существует
существует
 .
Это позволяет ввести в
понятие длины вектора.
.
Это позволяет ввести в
понятие длины вектора.
Длиной
вектора
называется число
 .
.
Очевидно,
если
,
то
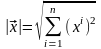 ,
т. е., как и в школьной математике, длина
вектора равна корню квадратному из
суммы квадратов его координат.
,
т. е., как и в школьной математике, длина
вектора равна корню квадратному из
суммы квадратов его координат.
Приведем без доказательства еще два свойства скалярного произведения (доказывать их будем в 6-й главе).
Неравенство Коши – Буняковского:
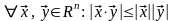 ,
или
,
или
 ;
;
неравенство треугольника:
 ,
или
,
или
 .
.
Из
неравенства Коши – Буняковского
вытекает, что для всех ненулевых векторов
пространства
выполняется неравенство
 ,
что дает возможность ввести понятие
угла между векторами.
,
что дает возможность ввести понятие
угла между векторами.
Углом
между ненулевыми векторами
и
 пространства
называется угол
пространства
называется угол
 такой, что
такой, что

Введем еще в понятие расстояния между точками.
Расстоянием
между точками М
и N
в пространстве
называется число
 .
Если
.
Если
 ,
а
,
а
 ,
то
,
то
 .
.
Таким образом, как и в школьной математике, расстояние между двумя точками в пространстве равно корню квадратному из суммы квадратов разностей их соответствующих координат.
