1. Определение линейного пространства и простейшие следствия из аксиом.

Определение. Линейным (векторным) пространством над полем Р называется множество V элементов произвольной природы, в котором заданы две операции: внутренняя – сложение, и внешняя – умножение на числа из Р , причем эти операции удовлетворяют следующим аксиомам.

1*. – коммутативность сложения.

2*. – ассоциативность сложения.

3*. существование нейтрального элемента).

4*. – существование противоположного элемента.

5*. .

6*. .

7*. .

8*. .

1º. В линейном пространстве существует единственный нейтральный элемент.

► Предположим, что в некотором линейном пространстве есть два нейтральных элемента: и . Тогда

Итак, мы пришли к противоречию.◄

2º. В линейном пространстве, каждый элемент имеет единственный противоположный.

►Предположим, что некоторый элемент имеет два различных противоположных: и , т. е. . Получаем

–

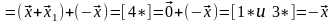опять пришли к противоречию.◄

3º.

► ◄

Замечание. При доказательстве следствий можно использовать либо аксиомы, либо уже доказанные следствия.

4º.

►

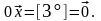
Таким образом, – противоположный к . Поэтому на основании 2-го следствия ◄

5º.

2. ► ◄

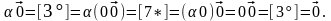3. 6º. В линейном пространстве из равенства 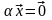вытекает: либо , либо .

4. ►а) – утверждение верно.

5. б) Тогда имеем:

6. ◄

2.Определение линейной зависимости и независимости элементов линейного пространства. Свойства линейной зависимости и независимости.

Определение. Система элементов

(3.1)

линейного пространства над полем Р называется линейно зависимой, если существуют числа из поля Р, не все равные 0, такие что

. (3.2)

Система (3.1) называется линейно независимой, если равенство (3.2) выполняется только в том случае, когда

, (3.3)

т. е. когда из равенства (3.2) вытекает (3.3).

1º. Система, содержащая нейтральный элемент, линейно зависима.

►Пусть система

(3.9)

содержит нейтральный элемент и пусть, например, . Положим

(3.10)

Среди чисел (3.10) есть отличные от нуля и

значит, система (3.9) линейно зависима. ◄

2º. Система, содержащая линейно зависимую подсистему, линейно зависима.

►Пусть система (3.9) содержит линейно зависимую подсистему и пусть, например, подсистема при линейно зависима. Это означает, что существуют числа

, (3.11) не все равные 0, такие что . Положим

(3.12)

Среди чисел (3.12) есть отличные от 0, так как таковые есть среди чисел (3.11), и

.

Таким образом, исходная система линейно зависима. ◄

Следствие. Любая подсистема линейно независимой системы линейно независима.

3º. Критерий линейной зависимости. Для того чтобы система векторов была линейно зависимой, необходимо и достаточно, чтобы один из векторов можно было представить в виде линейной комбинации остальных.

►Необходимость. Дано: система линейно зависима. Значит, существуют числа , не все равные 0, такие, что справедливо равенство

. (3.13)

Пусть, например, Тогда из (3.13) можно выразить :

что и требовалось доказать.

Достаточность. Дано: один из векторов можно представить в виде линейной комбинации остальных, например, Положим

(3.14)

Cреди чисел (3.14) есть отличные от 0 и , значит, исходная система линейно зависима. ◄

4º. Пусть система

(3.15)

линейно независима, а система

– (3.16)

линейно зависима. Тогда можно представить в виде линейной комбинации элементов системы (3.15).

►В силу линейной зависимости системы (3.16) существуют числа не все равные 0, такие, что

(3.17)

Предположим, что Значит, среди чисел есть отличные от нуля, и из (3.17) вытекает, что что противоречит линейной независимости (3.15). Таким образом, , и из (3.17) получаем требуемое утверждение.◄

5º. Для того чтобы система из одного элемента была линейно зависимой, необходимо и достаточно, чтобы он был нулевым.

►Достаточность вытекает из первого свойства.

Необходимость. Пусть система линейно зависима, тогда существует число такое, что . Значит, на основании 6-го следствия из аксиом (§1) .◄

Следующие свойства формулируем для пространства свободных векторов.

6º. Для того чтобы два вектора были линейно зависимыми, необходимо и достаточно, чтобы они были коллинеарными.

7º. Для того чтобы три вектора были линейно зависимыми, необходимо и достаточно, чтобы они были компланарными.

►Доказательство последних двух свойств вытекает из третьего свойства и критериев коллинеарности и компланарности из аналитической геометрии. ◄