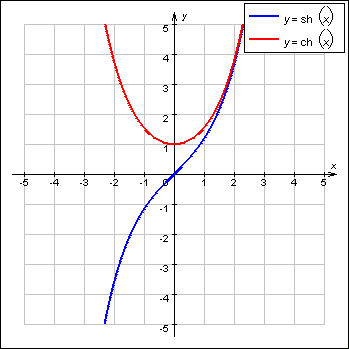
14.Гіперболічні функції та їх диференціювання
(гиперболический синус),
(гиперболический косинус).
Иногда рассматривается также гиперболический тангенс:
Г. ф. связаны между собой соотношениями, аналогичными соотношениям между тригонометрическими функциями:
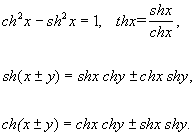
Г. ф. можно выразить через тригонометрические:
sh x + ch x = ex
|
15. Логарифмічне диференціювання. Диференціювання складної показникової функції.
Якщо
необхідно продиференціювати добуток
кількох функцій або дріб, чисельник та
знаменник якого містять добуток, часто
доцільні-ше обидві частини виразу
спочатку прологарифмувати за основою
е, а потім приступити до диференціювання .
Цей спосіб одержав назву логарифмічного
диференціювання . Похідна від
логарифма функції називається
логарифмічною похідною.Б
Производной
от функции 
называется
конечный предел отношения приращения
функции к приращению аргумента, когда
последнее стремится к нулю:
,
или 
.
Дифференцирование
многих функций значительно упрощается,
если их предварительно прологарифмировать.Если
требуется найти 
из
уравнения 
,
то можно
а)
логарифмировать обе части уравнения 
.б)
дифференцировать обе части полученного
равенства, где 
есть
сложная функция от 
, 
в)
заменить 
его
выражением через
и
определить
: 
Логарифмическое
дифференцирование полезно применять,
когда заданная функция содержит
логарифмирующиеся операции (умножение,
деление, возведение в степень, извлечение
корня) и, в частности, для нахождения
производной от показательно-степенной
функции 
,
где 
и 
–
функция от
.
Производные от функции, заданной параметрически
Если
функция
от
независимой переменной
задана
через посредство вспомогательной
переменной (параметра) 
: 
,
то производные от
по
определятся
следующими формулами: 
; 
.
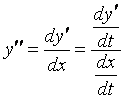Правило дифференцирования сложной функции
Сложная функция (композиция функций , суперпозиция функций )
обозначается 
или 
.
Производная композиции равна:
Если необходимо взять производную от композиции трех и более функций , то последовательно применяем указанное выше правило.
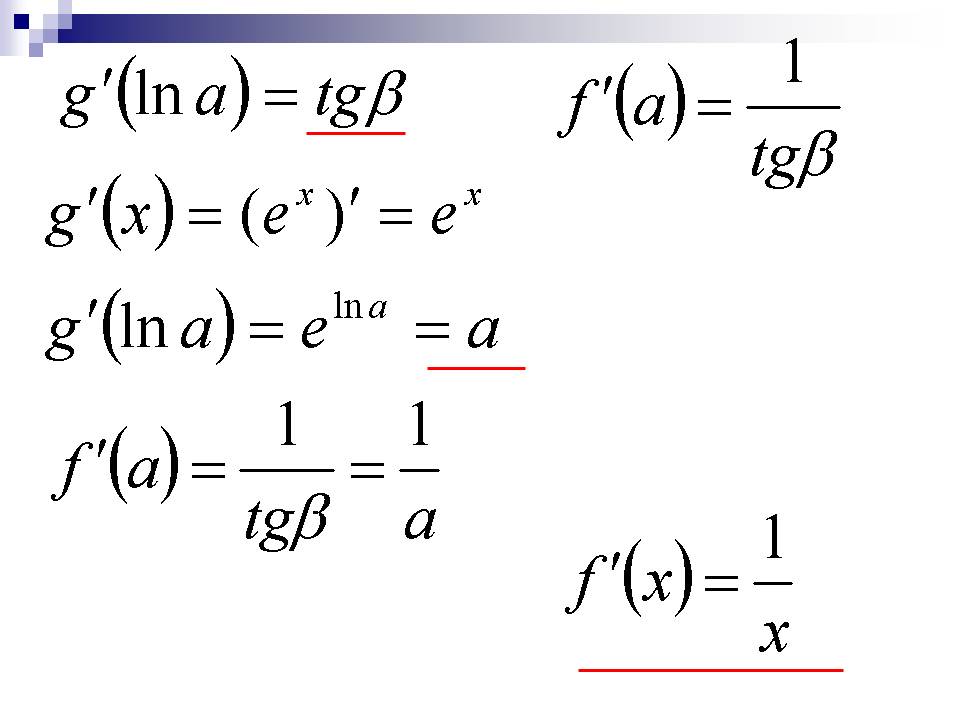
16(17). Диференціал функції.
Пусть
функция у=ƒ(х) имеет в точке х отличную
от нуля производную.
Тогда,
по теореме о связи функции, ее предела
и бесконечно малой функции, можно
записать D у/Dх=ƒ'(х)+α, где α→0 при
∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.Таким
образом, приращение функции ∆у
представляет собой сумму двух слагаемых
ƒ'(х)•∆х и а•∆х, являющихся бесконечно
малыми при ∆x→0. При этом первое слагаемое
есть бесконечно малая функция одного
порядка с ∆х, так как
а
второе слагаемое есть бесконечно малая
функция более высокого порядка, чем
∆х:
Поэтому
первое слагаемое ƒ'(х)· ∆х называют главной
частью приращения функции
∆у.Дифференциалом функции у=ƒ(х) в
точке х называется главная часть ее
приращения, равная произведению
производной функции на приращение
аргумента, и обозначается dу или
dƒ(х)):dy=ƒ'(х)•∆х.
Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу можно записать так:dy=ƒ'(х)dх,
Пример
24.2Найти дифференциал функции
Вычислить
dy при х=0, dx=0,1.Решение:
Подставив х=0 и dx=0.1, получим
Геометрический смысл дифференциала функции
Выясним геометрический смысл дифференциала.
Для
этого проведем к графику функции у=ƒ(х)
в точке М(х; у) касательную МТ и рассмотрим
ординату этой касательной для точки
х+∆х (см. рис. 138). На рисунке ½ АМ½ =∆х,
|AM1|=∆у. Из прямоугольного треугольника
МАВ имеем:
Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х.Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.
Применение дифференциала к приближенным вычислениям
Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство
∆у≈dy
причем это равенство тем точнее, чем меньше ∆х.
Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (24.3) широко применяется в вычислительной практике.