9. Похідна. Означення. Геометричний та фізичний зміст. Односторонні та нескінченні похідні.

 Похідна́  — основне поняття диференційного числення, що характеризує швидкість зміни функції. Визначається як границя відношення приросту функції до приросту її аргументу коли приріст аргументу прямує до нуля (якщо така границя існує). Функцію, що має скінченну похідну , називають диференційовною. Нехай в деякому околі точки x0 визначена функція f. Якщо ми візьмемо довільне число x в цьому околі, то приріст аргументу (позначається Δx) в цьому випадку визначається як x−x0, а приріст функції (Δy) — як f(x)−f(x0). Тоді, якщо існує границя  , то вона називається  похідною  функції f в точці x0.

 Похідною  функцією даної функції називається функція, що в будь-якій точці області визначення дорівнює  похідній  даної функції в цій точці.

Тригонометричні функції:

Обернені тригонометричні функції:

 Означення .  Похідною  функції  за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.

Операція знаходження  похідної  називається диференціюванням цієї функції.

Користуючись  означенням   похідної , знайти  похідні  функцій.

Приклад. Функція у = х2. Знайти  похідну  в точках х = 3 і х = – 4.

10. Теорема про зв ҆ язок між існуванням похідної та неперервністю функції в точці

11. Правила диференціювання

При  дифференцировании  константу можно выносить за производную:     Правило   дифференцирования  суммы функций:     Правило   дифференцирования  разности функций:     Правило   дифференцирования  произведения функций ( правило  Лейбница):     Правило   дифференцирования  частного функций:     Правило   дифференцирования  функции в степени другой функции:    Правило   дифференцирования  сложной функции:     Правило  логарифма при  дифференцировании  функции: 

Пусть  , тогда:

 

 

12. Таблиця похідних

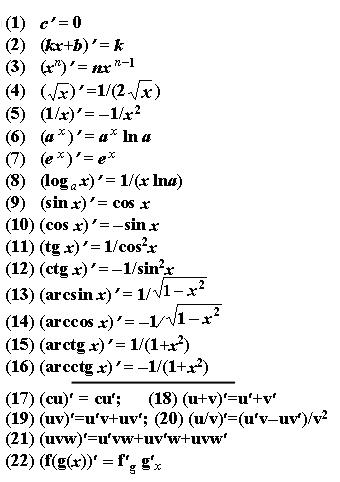
13. Обернена функція, її існування та диференціювання. Похідні обернених тригонометричних функцій.

 Обернена   функція  ( обернене  відображення) до даної  функції  f — в математиці така  функція  g, яка в композиції з f дає тотожне відображення.

Нехай f: X → Y та g: Y → X деякі  функції  (відображення).

Якщо композиція  функцій  f o g = EY, де E: Y→Y - тотожне відображення, то f має назву лівого  оберненого  відображення ( функції ) до g, а g - правого  оберненого відображення ( функції ) до f.

Якщо справедливо і f o g = EYі g o f = EX, то g має назву  оберненого  відображення ( оберненої   функції ) до f і позначається як f-1. Тобто f-1(f(x))=f(f-1(x))=x.

Не слід плутати позначку f-1 з позначенням степеня.

Наприклад, для  функції , визначеної як f(x) → 3x + 2,  оберненою   функцією  буде x → (x - 2) / 3. Це часто записується як:

найдем по правилу  дифференцирования   обратной   функции   .Окончательно,  .

Итак, Полученную функцию   можно рассматривать как функцию, заданную параметрически:  .

Используя эту формулу, можно находить и производные высших порядков функций, заданных параметрически. Найдем  . По определению второй производной  . Учитывая, что yx' есть функция параметра t, yx'=f(t),получаем: