Пропущена формула

Here k1 is an algebraic adjunct to an element of the k-th line and l-th column; Mk1 – is an element minor of the k-th line and l-th column obtained by deleting the k-th line and l-th column from the determinant .

Then according to (5.9) we have expression

(5.10)

Similarly

(5.11)

Voltage across load Z1is

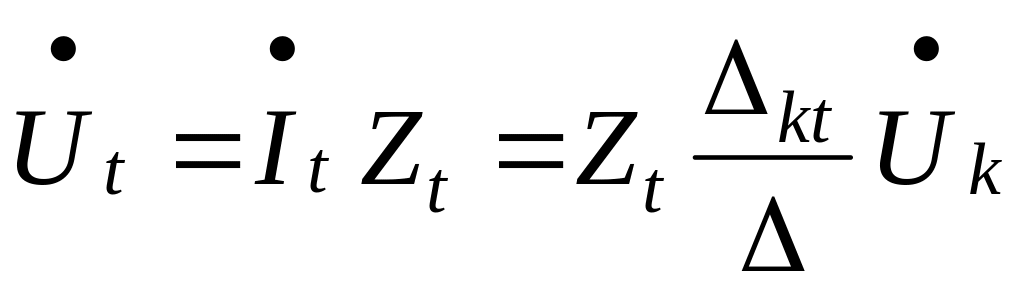(5.12)

From (5.10)-(5.12) we can define the circuit complex functions. From (5.11) we get the complex input impedance and complex input admittance

пропущена формула

From (5.10) we get the complex transfer admittance

пропущена формула

From (5.11) , (5.12) we get the complex transfer impedance

пропущена формула

From (5.12) we get the complex transfer coefficient by voltage

пропущена формула

From (5.10), (5.11) we get the complex transfer coefficient by current

пропущена формула

Thus , the circuit complex functions can be expressed by elements of the loop resistances matrix compiled for the passive circuit N and the load resistance Z1.

A determinant of the N-th order  is

. (5.13)

Here : q = 1 , 2, … , N- the number of lines of a determinant ;  , r,…, v are the permutations from N! of all possible permutations from the number 1 , 2 , … , N. The number q is at the sometime the number of inversions in each permutation. It is obvious that the number of terms in (5.13) is also equal to N!

Any of the loop resistances in (5.13) Zl , Z2r , … , ZNv can imaginary frequency j

(5.14)

where = 1 , 2 , … ,N.

It is evident that the determinant  that consists of that loop resistances Zi , Z2r , … , ZNv is also the rational function of the imaginary frequency j. The same can be said about the determinants kl , kk. Therefore , the complex functions of the circuit are the rational functions of the imaginary frequency j. Coefficients in the circuit complex functions according to (5.14) are determined only by the circuit parameters r , L , C and , consequently , are real coefficients.

Obtain the circuit complex functions according to Fig. 5.2 with the method of node voltages. Set the nodes K’ and l’ be connected between themselves. Assume the point of their connection to be the basis node. The voltages Uk , Ul will be considered as node voltages. Write a system of node equations according to circuit in Fig. 5.2:

(5.15)

Here N is the total number of independent nodes. Because the circuit is passive , the loop current Yint , Eint only in the k-th line of the system (5.33) is presented, where Yint is the internal conductance of the current source connected with k-th node.

The remaining nodes don’t have an energy source. The conductances Yjj , Yjk are intrinsic conductors and transfer conductance of the nodes. The voltages U1 , U2 , … UN are node voltages.

For the k-th node

(5.16)

where Y’kk is the intrinsic conduction of the k-th node without due regard for conductance Yint. That is Y’kk is the conductance of the N circuit the side of terminals k-k’.

For the k-th node , we can write the following according to Kirchoff’s current law:

пропущена формула

where

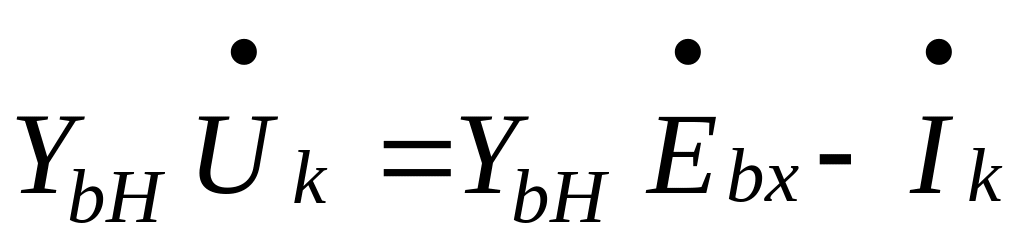(5.17)

Set us consider the k-th equation in (5.15)

(5.18)

Here with taking into account (5.16) and (5.17) we have:

пропущена формула

Then , (5.18) one can rewritten in such way

пропущена формула

or

пропущена формула.

Now the system of equations (5.15) have the following form:

(5.19)

Solution of the system of equations (5.19) for l-th voltage is:

(5.20)

where  is a determinant of the system of equations for the matrix of loop conductivities; l is a determinant of  in which the l-th column is replaced with the column of absolute terms – nodes’ currents.

Expand the determinant 1 by elements of the l-th column. Taking into account that absolute term Uk is only in the k-th line we get

пропущена формула

Then according to formula (5.20)

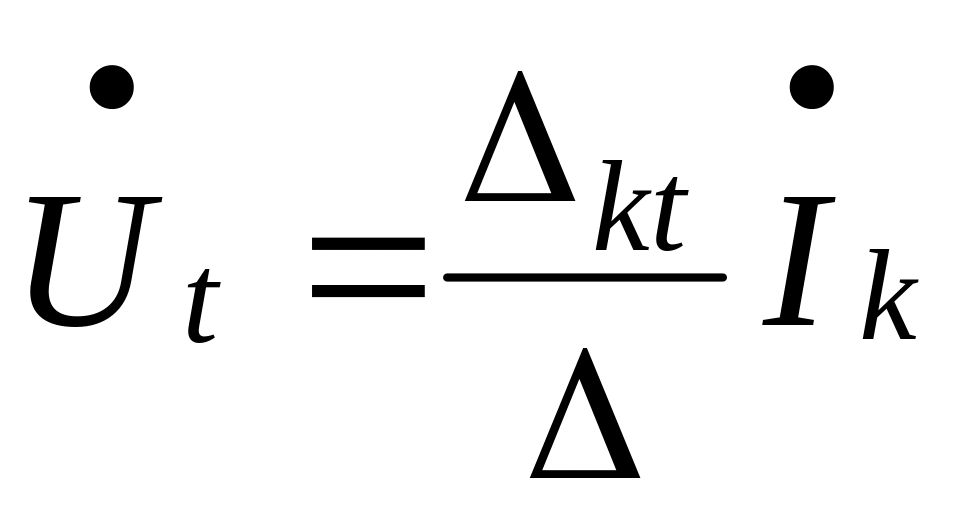(5.21)

Similarly

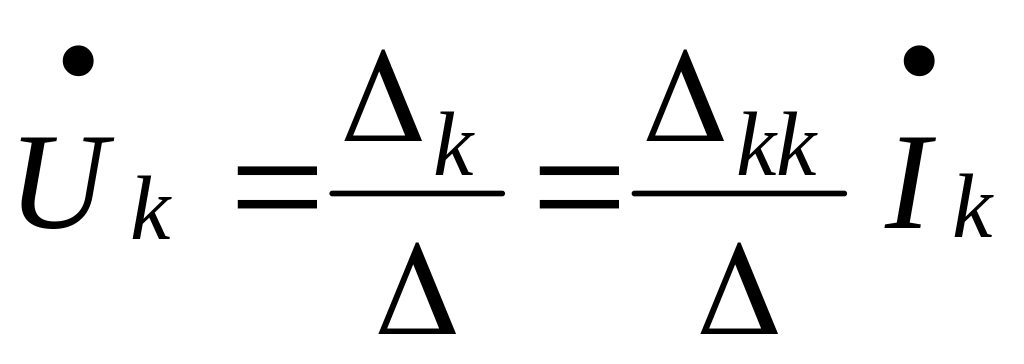(5.22)

Current in resistance Zl is:

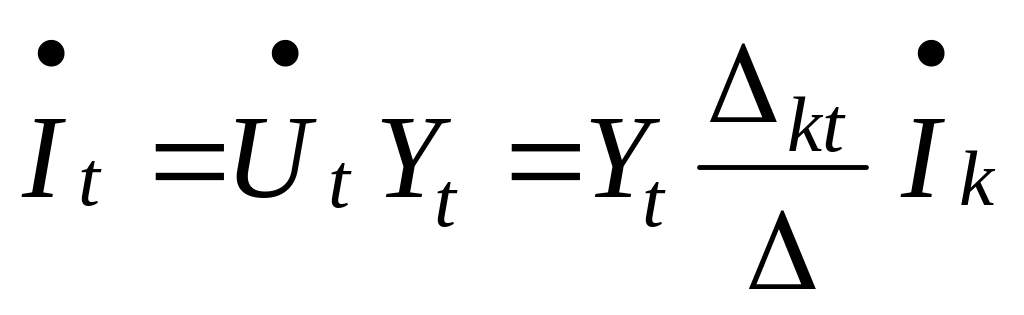,(5.23)

where Yl = 1/Zl is a conductivity of resistance.

From the formulae (5.21) and (5.23) we get the CFC, from formula (5.22) we find

complex input impedance and complex input admittance:

пропущена формула

From the formula (5.21) we get the complex transfer impedance:

пропущена формула

From the formulae (5.22) – (5.23) we get the complex transfer admittance:

пропущена формула

From the formula (5.23) we get the complex transfer current coefficient:

пропущена формула

From the formulae (5.21) and (5.22) we get the complex transfer voltage coefficient:

пропущена формула

Thus , the circuit complex functions CFC can be expressed by elements of the loop resistances matrix compiled for the passive circuit N and the load conductance Y1.

A determinant  of the N-th order is:

пропущена формула

Determination of node admittance is provided as in equation (5.14):

пропущена формула

Comparing the expressions for CFC getting with the Contour Current Method (CCM) and Node Voltage Method (NVM) we find relations:

пропущена формула

5.2.Components of complex functions and circuit frequency

characteristics

Circuit complex functions CFC as any complex number can be represented in the algebraic, exponential and trigonometric forms:

пропущена формула

where

пропущена формула

• is the real part of a complex function ;

пропущена формула

• is the imaginary part of a circuit complex function ;

пропущена формула

• is the argument of a circuit complex function.

пропущена формула

• is the module of a circuit complex function.

The quantities R() , X() , φ() , K() depend on the frequency and are called as a real (RFC) , imaginary (IFC) , phase (PFC) and amplitude (AFC) frequency characteristics respectively. They are plotted against the frequency  - along to the abscissa axis and the frequency characteristic – along to the ordinate axis.

For example , for a r , L , C series circuit the typical AFC and PFC have the forms according to Fig. 5.3.a and Fig. 5.3. b.

Fig. 5.3

The amplitude – frequency (AFC) and phase – frequency (PFC) characteristics can be united into one amplitude – phase – frequency characteristic (APFC). It is plotted in relation to the coordinates X() , R() when the frequency  is changed from 0 up to  or , in a common case , from ”-” up to . Each value of frequency has a value R() which is laid off along the abscissa and X(w) is laid off along the ordinate axis. The values X() and R() define a point on the plane X(), R().The geometric location of the points which are obtained which different values of W make the APFC plot. Fig 5.4 shows an APFC plot for a circuit of the second order. Here at =0 the value X(0)=0.Since R(0)=0,the point of the characteristic is on the abscissa. When the frequency is increased the X() values appear and the R() values decrease. So, at  = ₁ we have that X(₁)<0 and R(₁)<R(0). At ₂>₁, we get the following point of the characteristic in the same way, and so on. At  =  the functions X()=0 and R()=0, and the characteristic point coincides with the beginning of the coordinates axes.

Fig.5.4

Quite often APFC is supplemented by a curve at <0.In this case in Fig.5.4 there appears a dotted curve which is symmetrical to the characteristic at >0.

APFC can be built also by calculating the module K() and argument φ() at each value of the frequency . Tying off the segment K() in the direction φ() we get the characteristic point.

At the end of the segment an arrow is placed and we say that with frequency changing the vector K() describes a curve which is called the frequency locus. The arrow on the curve indicates the direction in which the frequency  increases. Sometimes the frequency locus is called also the Nyquist diagram.

In the theory of electric filters for the circuit complex functions the exponential form of notation is used.

(5.24)

Here χ(j)= α() + jβ() - is the complex coefficient of distribution.

Taking the logarithm from expression (5.24) we get:

пропущена формула

or

(5.25)

The value α() is called the logarithmic amplitude-frequency characteristic (ALFC).If it is calculated through the natural logarithm, then the value is measured in Napiers. If α() is calculated through the decimal logarithm, then the unit of measurement is called the Bell (B):

пропущена формула

Because

пропущена формула

then

пропущена формула

5.3. Frequency characteristics of simplest circuits.

5.3.1. Frequency characteristics of first-order circuits

Consider the simplest rC-circuit (Fig.5.5.a).Let us define the complex voltage transfer ratio:

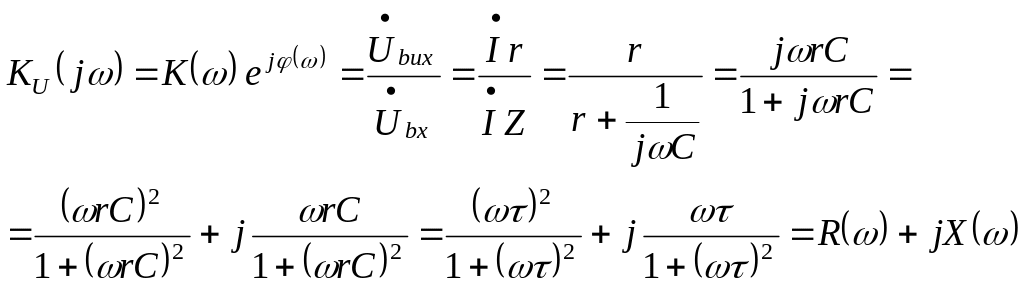_(5.26)

Fig.5.5

пропущены формулы и текст и рисунки (со стр. 130 )

Fig.5.6

Fig.5.7

If τ is denoted as time constant: τ = l/r, than

_(5.27)

The expression (5.84) coincides with (5.71) for the rC-circuit in Fig.5.5.a. Consequently, the frequency characteristics of the circuits in Fig.5.8.a and 5.5.a are identical.

The analysis shows that the frequency characteristics on the circuits in Fig.5.8.b and 5.5.b are also identical.

5.3.2. Frequency characteristics of second- and third-order circuits

Consider the second-order circuit in Fig.5.9.The matrix of node conductances for this circuit is as follows:

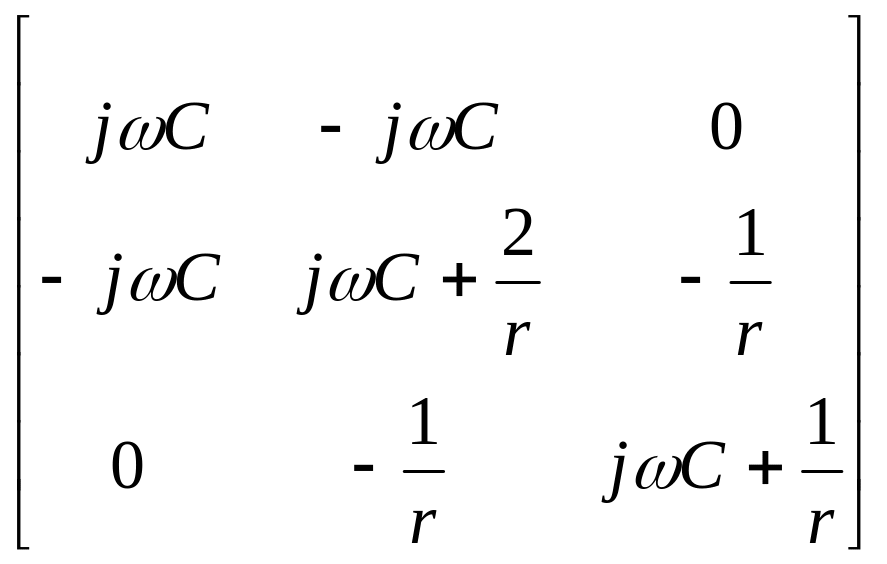_(5.28)

Fig. 5.8 Fig.5.9

Hence, the algebraic adjuncts ₁₃ and ₁₁ are: