Chapter 5. Frequency characteristics of circuits

5.1. Complex function of a circuit

5.1.1. The notion of the complex function of a circuit

The application of exponential functions allows us to introduce the notion of the complex function of a circuit which is used for describing circuits not containing independent sources of energy.

In a common case, the signal x_out at the output of an electric circuit (circuit reaction) is connected with the input signal x_in (action) by relation

(5.1)

The harmonic functions x_in, x_out can be represent as images by complex numbers simiear to

(5.2)

Replace in (5.1) the real quantities x_in ,x_out with their complex instantaneous quantities according to relation (5.2):

……………… пропуск формулы………………………………………………………………

The ration of reaction to action when they are given as an exponential function of imaginary frequency j is called the complex function of a circuit (CFC) K(j):

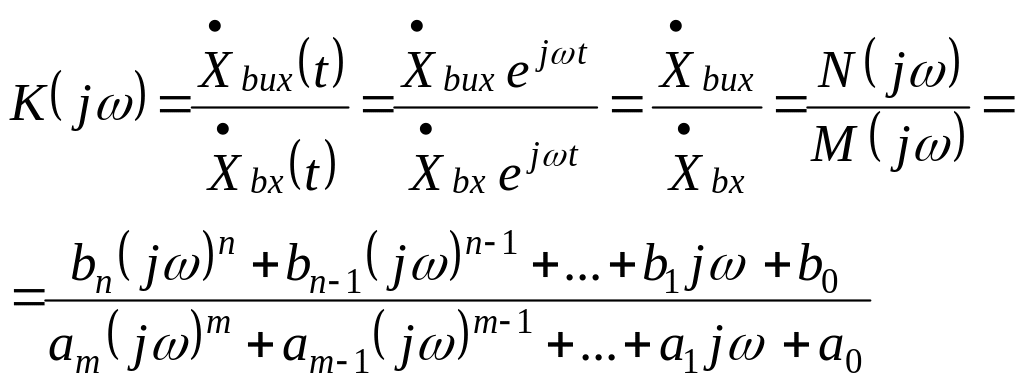(5.3)

Пропуск формулы

That is, the complex function of a circuit determines the circuit reaction to the action of exponential function of the imaginary frequency j in the state established.

With the help of the complex function, the theory of analytical functions of the complex variable is linked to the analysis of electric circuits.

Under analyzing of electric circuits, we set up an equation system in which it is always possible to identify two main quantities of action and reaction, for example, current in one branch and voltage in the another.

Fig. 5.1

Consider the types of complex functions of a circuit. Fig. 5.1 shows a diagram of the passive , linear circuit N with the marked input (1-1)and output (2-2) terminals. The diagram indicates input and output currents and voltages and also the load impedance Z_h connected to the output terminals. There are input and transfer complex functions of a circuit.

The input complex function of a circuit is the relation of complex images of voltage and current acting on the terminals of the circuit.

They are as follows :

- complex input impedance

пропуск формулы

- complex input admittance

пропуск формулы

It’s obvious that

пропуск формулы

The transfer complex function of a circuit is the relation of complex images of voltage and current acting on different pairs of circuit terminals.

They are as follows :

- complex voltage transfer ratio

пропуск формулы

- complex current transfer ratio

пропуск формулы

- complex transfer impedance

пропуск формулы

- complex transfer admittance

пропуск формулы

It’s evident that

пропуск формулы

5.1.2. Connection between complex functions and circuit parameters

Fig 5.2 shows a diagram of the passive linear circuit N with two marked pairs of K-K’ ,1-1’ terminals. The voltage source , the EMF of Which is equal to Ein , and the internal resistance is equal to Zint is connected to the terminals l-l’. Find the ratio of currents and voltages in this circuit. Write down the equation system a ecovding to the method of loop currents. Mark out at terminals l-l’ – the l-th loop with the loop current t1 , at terminals K-K’-the K-th loop with the loop current Ik. Indicate directions of loop tracing. And as a result we get.

(5.4)

Fig.5.2

Here N is the total number of independent circuit loops , see Fig. 5.2. Since the circuit is passive, the loop EMF Ein is contained only in the K-th line (5.12) of the system ,the other loops do not contain no independent energy sources. The resistances Zji , Zjk are the internal and mutual resistances of the loops. The currents I1,I2,.. Ik ,…, In are the loop currents.

For the k-th loop

, (5.5)

where Z’kk is the internal resistance of the k-th loop without taking into account resistance Zint. That is Z’kk is the resistance of the circuit N on the side of terminals K-K’.

For the k-th loop we can write the following to Kirchoff’s voltage law:

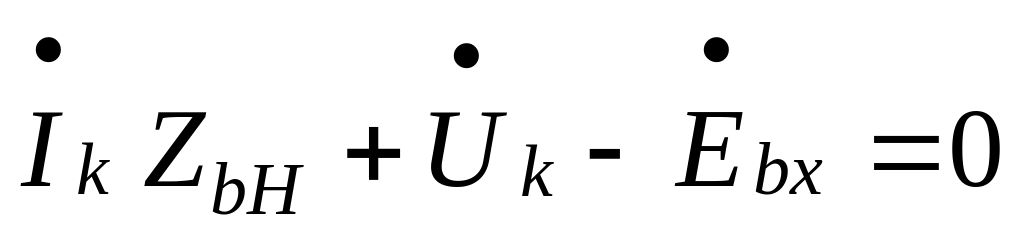. (5.6)

From equation (5.6) we have relation

пропущена формула

Let us consider the k-th equation in system of equations (5.4)

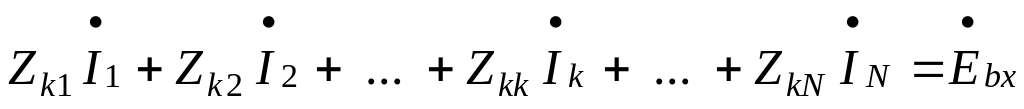(5.7)

From expressions (5.5) and (5.6) we have

пропущена формула

Then equation (5.7) can be rewritten as

пропущена формула

or

пропущена формула.

So, system of equations (5.4) is:

(5.8)

_________________________________________________________________________

According to Cramer’s rule the solution (5.8) for the l’s current is

, (5.9)

where  is a determinant of the system for the matrix of loop resistances; l is a determinant of  in which the l-th column is replaced by the column of absolute terms – loop EMF.

Expand the determinant 1 by elements of the l-th column. Taking into account that absolute term Uk is only in the k-th line we get