Математическое описание многофазной гетерогенной среды

1. Основные допущения

Неравновесная термодинамика, в отличие от равновесной, базируется на теории поля. В качестве аппарата теории поля рассмотрим механику гетерогенных сред и дадим математическое описание процессов с фазовыми переходами и химическими реакциями, происходящими в полидисперсных гетерогенных средах.

Рассмотрим многофазную полидисперсную среду, где одна фаза (сплошная, несущая)  газ или жидкость, а другие фазы (дисперсные r-фазы) – включения твёрдых частиц, капель жидкости или газовых пузырьков, размеры (объёмы) которых изменяются от r – dr до r + dr. Дисперсность гетерогенной фазы характеризуется функцией , так что – число включений в единице объёма смеси, размеры (объёмы) которых – от r до r + dr. В каждой из r-фаз размеры (объёмы) включений остаются постоянными, меняется только их число.

Движение смеси будем изучать при следующем допущении: расстояния, на которых параметры течения смеси меняются существенно (вне поверхности разрыва), много больше размеров включений и расстояний между ними [6, 7].

В отличие от гомогенной смеси, где каждый компонент рассматривается как занимающий весь объём смеси равномерно с другими компонентами, в гетерогенной смеси каждая фаза занимает лишь часть объёма смеси. В связи с этим возникает необходимость введения объёмных долей фаз и средних плотностей фаз в каждой точке объёма, занятого смесью:

где V – объём смеси,  – плотность смеси; – объём i-й фазы, – истинная и средняя плотности i-й фазы, – объёмное содержание (объёмная доля) i-й фазы; R – наибольший размер (объём) включений; индекс 1 относится к несущей (сплошной) фазе, индекс 2  к дисперсной (гетерогенной) фазе.

На основании введённого допущения можно принять, что несущая фаза и все r-фазы  континуумы, заполняющие один и тот же объём и имеющие каждая свою плотность, массу, скорость, температуру. Введение многоскоростного континуума необходимо, так как скорости относительного движения фаз в смеси по порядку могут быть равны скоростям их абсолютного движения. Первую фазу будем описывать моделью вязкой жидкости. В качестве тензоров поверхностных сил и тензоров вязких напряжений примем [8]:

где – символ Кронекера; P – давление; – тензор скоростей деформаций несущей фазы; – коэффициенты вязкости, – вектор средней массовой скорости сплошной фазы.

Введя основные допущения, перейдём к математическому описанию мас­сообменных химико-технологических процессов, происходящих в полидисперсных средах, в рамках многоскоростной модели. Запишем уравнения сохранения массы, импульса, энергии с учётом фазовых переходов на включениях [6] (данная система уравнений пригодна для математического описания процессов кристаллизации, сушки, экстракции, ректификации).

2. Уравнения сохранения массы

Уравнение сохранения массы для сплошной фазы имеет вид:

(2.1)

Закон сохранения массы для дисперсной фазы отражает уравнение баланса числа включений с учётом изменения объёма включения за счёт фазового перехода:

(2.2)

Отметим, что уравнение (2.2) записано для r-фазы. Для получения уравнения сохранения массы всей дисперсной фазы надо умножить каждый член уравнения (2.2) на и проинтегрировать его по dr от 0 до R.

При написании уравнений (2.1) и (2.2) использованы следующие обозначения: – наблюдаемая скорость изменения размера (объёма) включения; R – наибольший размер включений; – средняя плотность сплошной фазы; – истинная плотность дисперсной фазы; – число включений в единице объёма смеси с размером от r до r + dr; – вектор средней массовой скорости i-й фазы (здесь и далее векторные величины в формулах выделяются полужирным шрифтом):

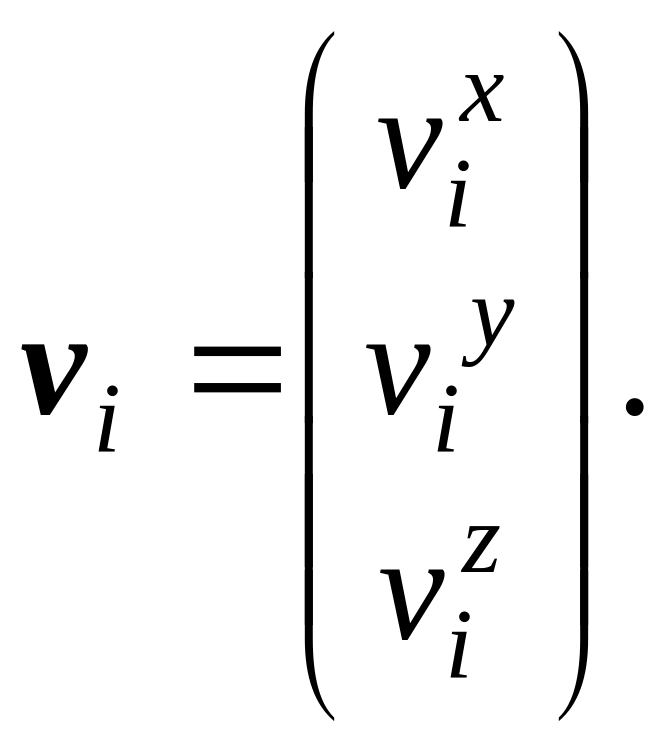
Вторые члены в левых частях уравнений (2.1) и (2.2) учитывают движение смеси. Дивергенцию можно представить более подробно:

где – проекции вектора средней массовой скорости i-й фазы на оси координат.

Член в правой части уравнения (2.1) и третий член в левой части уравнения (2.2) отражают суммарное влияние фазового перехода на включениях.