
- •Методи побудови загальної лінійної моделі
- •4.2. Специфікація моделі
- •4.3. Передумови застосування методу найменших квадратів (1мнк)
- •4.4. Оператор оцінювання 1мнк
- •4.5. Властивості оцінок параметрів
- •4.6. Коваріаційна матриця оцінок параметрів моделі
- •4.7. Прогноз залежної змінної.
- •4.8. Оцінювання прогнозних можливостей моделі
- •4.9. Побудова економетричної моделі на основі покрокової регресії
- •4.10. Коефіцієнти детермінації і кореляції
- •4.11. Частинні коефіцієнти кореляції та коефіцієнти регресії
- •4.12. Перевірка значущості та інтервали довіри
- •4.12.1. Значущість економетричної моделі. Гіпотезу про рівень значущості зв’язку між залежною і пояснювальними змінними можна перевірити за допомогою f-критерію:
- •Мультиколінеарність
- •6.2. Основні наслідки мультиколінеарності
- •1. Дисперсія і коваріація оцінок параметрів моделі різко збільшуються.
- •2. Похибки оцінок параметрів значно збільшуються, відповідно збільшуються їхні інтервали довіри.
- •6.3. Ознаки мультиколінеарності
- •6.4. Алгоритм Фаррара—Глобера
- •Гетероскедастичність
- •7.2. Наслідки гетероскедастичності
- •7.3. Методи визначення гетероскедастичності
- •7.4. Визначення матриці s
- •7 .5. Узагальнений метод найменших квадратів (метод Ейткена)
- •7.6. Прогноз
- •1. Дослідимо гетероскедастичність на основі тесту Гольфельда—Квандта.
- •Автокореляція
- •8.2. Перевірка наявності автокореляції
- •8.3. Оцінвання параметрів моделі з автокорельованими залишками
- •8.4. Прогноз
- •6.5. Методи звільнення від мультиколінеарності
7.3. Методи визначення гетероскедастичності
7.3.1. Перевірка гетероскедастичності за крите- рієм . Цей метод застосовується тоді, коли вихідна сукупність спостережень досить велика. Розглянемо відповідний алгоритм.
Крок
1. Вихідні
дані залежної змінної Y
розбиваються на k
груп
 відповідно до зміни рівня величини Y.
відповідно до зміни рівня величини Y.
Крок 2. За кожною групою даних обчислюється сума квадратів відхилень:

Крок 3. Визначається сума квадратів відхилень у цілому по всій сукупності спостережень:

Крок 4. Обчислюється параметр :

де n — загальна сукупність спостережень; nr — кількість спостережень r-ї групи.
Крок 5. Обчислюється критерій:
 (7.5)
(7.5)
який
наближено відповідатиме розподілу
при ступені свободи
 ,
коли дисперсія всіх спостережень
однорідна. Тобто якщо значення
,
коли дисперсія всіх спостережень
однорідна. Тобто якщо значення
 не менше за табличне значення
за вибраного рівня довіри і ступені
свободи
не менше за табличне значення
за вибраного рівня довіри і ступені
свободи
 то спостерігається гетероскедастичність.
то спостерігається гетероскедастичність.
група I |
група II |
група III |
0,36 |
0,41 |
0,82 |
0,20 |
0,50 |
1,04 |
0,08 |
0,43 |
1,53 |
0,20 |
0,59 |
1,94 |
0,10 |
0,90 |
1,75 |
0,12 |
0,95 |
1,99 |
Розв’язання
Крок 1. Розіб’ємо дані залежної змінної, які наведені в таблиці 7.1, на три групи, по шість спостережень у кожній.
Крок 2. Обчислимо суму квадратів відхилень індивідуальних значень кожної групи від свого середнього значення:
2.1.

2.2.
 ;
;  ;
;
 .
.
Крок 3. Знайдемо суму квадратів відхилень за всіма трьома групами:
 = S1 + S2 + S3 = 0,05313 + +
0,2822 + 1,1703 = 1,5056 .
= S1 + S2 + S3 = 0,05313 + +
0,2822 + 1,1703 = 1,5056 .
Крок 4. Обчислимо параметр

Крок 5. Знайдемо критерій

Цей
критерій наближено задовольняє розподіл
2
з k – 1 = 2
ступенями свободи. Порівняємо значення
критерію
з табличним значенням критерію 2
з k – 1 = 2
ступенями свободи за рівня довіри 0,99,
 =
9,21. Оскільки >
,
то дисперсія залишків буде змінюватись,
тобто для даних табл. 7.1 спостерігається
гетероскедастичність.
=
9,21. Оскільки >
,
то дисперсія залишків буде змінюватись,
тобто для даних табл. 7.1 спостерігається
гетероскедастичність.
7.3.2. Параметричний тест Гольдфельда—Квандта. У випадку, коли сукупність спостережень невелика, розглянутий вище метод застосовувати недоцільно.
У
такому разі Гольдфельд і Квандт
запропонували розглянути випадок, коли
 ,
тобто дисперсія залишків зростає
пропорційно до квадрата однієї з
незалежних змінних моделі:
,
тобто дисперсія залишків зростає
пропорційно до квадрата однієї з
незалежних змінних моделі:
Y = XA + u.
Для виявлення наявності гетероскедастичності згадані вчені склали параметричний тест, в якому потрібно виконати такі кроки.
Крок 1. Упорядкувати спостереження відповідно до величини елементів вектора Xj.
Крок 2. Відкинути c спостережень, які містяться в центрі вектора. Ця процедура дасть змогу порівняти дисперсії залишків для найменших та найбільших значень пояснювальної змінної. Згідно з експериментальними розрахунками автори знайшли оптимальні співвідношення між параметрами c і n для 30—60 спостережень, де n — кількість елементів вектора :
 .
.
Крок
3. Побудувати
дві економетричні моделі на основі
1МНК за двома утвореними сукупностями
спостережень обсягом
 ,
,
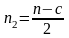 за умови, що обсяг
за умови, що обсяг
 і
і
 перевищує кількість змінних m.
Якщо
перевищує кількість змінних m.
Якщо
 то відкидається перше або останнє
спостереження сукупності.
то відкидається перше або останнє
спостереження сукупності.
Крок
4.
Знайти суму квадратів залишків за
першою (1) і другою (2) моделями
 і
і
 :
:
 ,
,
де
 — залишки за моделлю (1);
— залишки за моделлю (1);
 ,
,
де
 — залишки за моделлю (2).
— залишки за моделлю (2).
Крок 5. Обчислити критерій
 ,
(7.6)
,
(7.6)
який
у разі виконання гіпотези про
гомоскедастичність відповідатиме
F-розподілу
з
 ,
ступенями свободи. Це означає, що
обчислене значення R*
порівнюється з табличним значенням
F-критерію
для ступенів свободи
і
і вибраним рівнем значущості .
Якщо
,
ступенями свободи. Це означає, що
обчислене значення R*
порівнюється з табличним значенням
F-критерію
для ступенів свободи
і
і вибраним рівнем значущості .
Якщо
 ,
то гетероскедастичність відсутня.
,
то гетероскедастичність відсутня.
Приклад 7.3. У табл. 7.3 наведено дані про загальні витрати та витрати на харчування сімей. Для цих даних перевірити гіпотезу про наявність гетероскедастичності.
Витрати |
Загальні витрати, |
|
u |
u2 |
2,30 |
15 |
2,16 |
0,14 |
0,020 |
2,20 |
15 |
2,16 |
0,04 |
0,002 |
2,08 |
16 |
2,20 |
–0,12 |
0,015 |
2,20 |
17 |
2,25 |
–0,05 |
0,002 |
2,10 |
17 |
2,25 |
–0,15 |
0,022 |
2,32 |
18 |
2,29 |
0,26 |
0,0007 |
2,45 |
19 |
2,34 |
0,11 |
0,012 |
2,50 |
20 |
|
|
|
2,20 |
20 |
|
|
|
2,50 |
22 |
|
|
|
3,10 |
64 |
|
|
|
2,50 |
68 |
2,37 |
0,13 |
0,016 |
2,82 |
72 |
2,52 |
0,29 |
0,085 |
3,04 |
80 |
2,68 |
0,36 |
0,128 |
2,70 |
85 |
2,99 |
–0,29 |
0,084 |
3,94 |
90 |
3,18 |
0,76 |
0,573 |
3,10 |
95 |
3,38 |
–0,28 |
0,076 |
3,99 |
100 |
3,57 |
0,42 |
0,178 |
1. Ідентифікуємо змінні:
Y — вектор витрат на харчування, залежна змінна;
X — вектор загальних витрат, незалежна змінна.
Y = f (X, u).
2. Для перевірки гіпотези про наявність гетероскедастичності застосуємо параметричний тест Гольдфельда—Квандта.
2.1. Упорядкуємо значення незалежної змінної від меншого до більшого і відкинемо c значень, які містяться всередині впорядкованого ряду:
, c 4.
У результаті матимемо дві сукупності спостережень:


2.2. Побудуємо дві економетричні моделі на основі двох новостворених сукупностей спостережень.
2.3. Визначимо залишки за цими двома моделями:
 ;
;  .
.
Залишки та квадрати залишків наведено в табл. 7.3.
2.4. Обчислимо дисперсії залишків та знайдемо їх співвідношення:
 .
.
2.5.
Порівняємо критерій
 з критичним значенням F-критерію
при 1 = 5
і 2 = 5
ступенях свободи і значущості = 0,01
F( = 0,01)
= 11. Оскільки
>
з критичним значенням F-критерію
при 1 = 5
і 2 = 5
ступенях свободи і значущості = 0,01
F( = 0,01)
= 11. Оскільки
>  ,
то вихідні дані з імовірністю 0,99 мають
гетероскедастичність.
,
то вихідні дані з імовірністю 0,99 мають
гетероскедастичність.
7.3.4.
Тест Глейзера.
Ще один тест для перевірки
гетероскедастичності запропонував
Глейзер. Він розглядає регресію модуля
залишків
 ,
що відповідають регресії найменших
квадратів, як певну функцію від
,
де
— та незалежна змінна, яка відповідає
зміні дисперсії
.
Для цього використовуються такі види
функцій:
,
що відповідають регресії найменших
квадратів, як певну функцію від
,
де
— та незалежна змінна, яка відповідає
зміні дисперсії
.
Для цього використовуються такі види
функцій:
1)
 ;2)
;2)
 ;
;
3)
 4)
4)
 .
.
У
цих рівняннях
 — стохастична складова.
— стохастична складова.
Рішення
про відсутність гетероскедастичності
залишків приймається на підставі
статистичної значущості коефіцієнтів
 і
і
 Переваги цього тесту визначаються
можливістю розрізняти випадок чистої
і мішаної гетероскедастичності.
Переваги цього тесту визначаються
можливістю розрізняти випадок чистої
і мішаної гетероскедастичності.
Можливі чотири випадки:
 є
статистично значущими;
є
статистично значущими;— статистично значуща, — статистично незначуща оцінка;
— статистично значуща, — статистично незначуща оцінка;
— статистично незначущі.
У першому випадку залишки гетероскедастичні, причому існує чиста і мішана гетероскедастичність. У другому випадку залишки мають мішану гетероскедастичність. Третій випадок свідчить про наявність чистої гетероскедастичності. У четвертому випадку гетероскедастичність відсутня.
Місяць |
Y |
|
u |
u2 |
|
1 |
2,36 |
2,00 |
0,36 |
0,1296 |
|
2 |
2,20 |
2,06 |
0,14 |
0,0196 |
|
3 |
2,08 |
2,13 |
–0,05 |
0,0025 |
|
4 |
2,20 |
2,19 |
0,01 |
0,0001 |
|
5 |
2,10 |
2,24 |
–0,14 |
0,0196 |
|
6 |
2,12 |
2,34 |
–0,22 |
0,0484 |
|
Приклад 7.4. Нехай потрібно перевірити наявність гетероскедастичності для побудови економетричної моделі, яка описуватиме залежність між рівнем заощаджень і доходом. Вихідні дані наведено в табл. 7.4.
Приклад 7.4. Нехай потрібно перевірити наявність гетероскедастичності для побудови економетричної моделі, яка описуватиме залежність між рівнем заощаджень і доходом. Вихідні дані наведено в табл. 7.4.
Місяць |
Дохід, гр. од. |
Заощадження, гр. од. |
Місяць |
Дохід, гр. од. |
Заощадження, гр. од. |
1 |
10,8 |
2,36 |
10 |
17,5 |
2,59 |
2 |
11,4 |
2,20 |
11 |
18,7 |
2,90 |
3 |
12,0 |
2,08 |
12 |
19,7 |
2,95 |
4 |
12,6 |
2,20 |
13 |
20,6 |
2,82 |
5 |
13,0 |
2,10 |
14 |
21,7 |
3,04 |
6 |
13,9 |
2,12 |
15 |
23,1 |
3,53 |
7 |
14,7 |
2,41 |
16 |
24,8 |
3,44 |
8 |
15,5 |
2,50 |
17 |
25,9 |
3,75 |
9 |
16,3 |
2,43 |
18 |
27,2 |
3,99 |
Використаємо параметричний тест Гольдфельда—Квандта для встановлення гетероскедастичності у визначенні залежності між наведеними показниками.
Розв’язання. Ідентифікуємо змінні:
Y — заощадження — залежна змінна;
X
— дохід — пояснююча змінна,

Крок 1. Вихідна сукупність спостережень упорядковується відповідно до величини елементів вектора Х, який може впливати на зміну величини дисперсії залишків. Оскільки в табл. 7.3 дані про дохід упорядковані, то переходимо до наступного кроку.
Крок
2.
Відкинемо c
спостережень,
які розташовано в центрі векторів Х
і Y,
де
 ,
і поділимо сукупність спостережень на
дві частини, кожна з яких містить
,
і поділимо сукупність спостережень на
дві частини, кожна з яких містить
 спостережень.
спостережень.
Крок
3.
Побудуємо економетричну модель за
першою сукупністю, яка містить
спостереження від першого по сьомий
місяць включно:
 .
Система нормальних рівнянь для визначення
параметрів цієї моделі запишеться так:
.
Система нормальних рівнянь для визначення
параметрів цієї моделі запишеться так:

Звідси = 2,122; = 0,007.
Економетрична модель має вигляд
I:
 .
.
Крок 4. Побудуємо економетричну модель виду за другою сукупністю спостережень, починаючи від дванадцятого до вісімнадцятого місяця.
Система нормальних рівнянь для визначення параметрів цієї моделі запишеться так:

Звідси = – 0,408; = 0,165.
Економетрична модель має вигляд:
II:

Крок 5. Знайдемо розрахункові значення залежної змінної моделі — розміру заощадження за кожною з двох моделей, і визначимо відхилення фактичних значень заощаджень від розрахункових.
Таблиця 7.5 Таблиця 7.6
У табл. 7.5 наведено результати обчислення суми квадратів залишків за першою моделлю S1 = 0,2202.
У табл.7.6 наведено обчислення суми квадратів залишків за другою моделлю S2 = 0,3039.
Крок 6. Обчислимо критерій , який наближено відповідає F-розподілу:
 .
.
Порівняємо його значення з табличним значенням F-критерію за вибраного рівня довіри Р = 0,99 і ступенях свободи 1 = 5 і 2 = 5. Fтабл = 11. Звідси R* < Fтабл, що свідчить про відсутність гетероскедастичності.
7.3.5. Тест рангової кореляції Спірмена. Наявність чистої гетероскедастичності в сукупності спостережень можна виявити, розрахувавши рангові коефіцієнти кореляції Спірмена. На базі коефіцієнта Спірмена побудовано відповідний тест, алгоритм якого полягає в реалізації таких кроків:
Крок 1. Побудова простих економетричних моделей 1МНК залежної змінної (Y) з кожною з пояснювальних змінних (Хj).
Крок 2. Визначення вектора залишків для кожної з побудованих моделей (uj).
Крок
3.
Ранжування вектора кожної пояснювальної
змінної (Хj)
і кожного з векторів
 від меншого до більшого та заміна
компонентів цих векторів їхніми рангами.
від меншого до більшого та заміна
компонентів цих векторів їхніми рангами.
Крок 4. Визначення коефіцієнта рангової кореляції Спірмена за формулою:
 , (7.7)
, (7.7)
де
dij
— різниця між рангами xij
та
 ;
;
 ;
;
n — кількість спостережень; m – 1 — кількість пояснювальних змінних.
Крок 5. Розраховується t-статистика для визначення рівня статистичної значущості кореляції Спірмена за формулою:
 . (7.8)
. (7.8)
Доведено,
що ця характеристика має закон розподілу
Стью-
дента з кількістю ступенів
свободи
 .
.
Якщо розраховане значення t-статистики перевищує критичне значення при ступені свободи n – 2 та вибраному рівні значущості , то гіпотезу про наявність гетероскедастичності потрібно прийняти. У протилежному випадку вона відхиляється.
Розглянемо застосування тесту рангової кореляції для визначення наявності гетероскедастичності у статистичній інформації.
Приклад 7.5. Необхідно дослідити наявність гетероскедастичності у статистичній інформації, поданій в табл. 4.2 (приклад 4.2).
Розв’язання
1. Побудуємо прості економетричні моделі, що описують залежність між прибутком та кожним з чинників. Наведемо ці моделі:
1)  ;
;
2)  ;
;
3)  .
.
2. Розрахуємо залишки за цими економетричними моделями (табл. 7.7).
3.
Визначимо ранги для кожної з пояснювальних
змінних та залишків. Для цього кожну
змінну та кожний із залишків
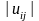 пронумеруємо порядковим номером від
одиниці до 20. Потім впорядковуємо кожну
пояснювальну змінну та залишки,
посортувавши їх від меншого до більшого
(Exel, меню «Данные», розділ «Сортировка»).
У результаті порядковий номер чисел
цих показників зміниться і характеризуватиме
ранг його в масиві.
пронумеруємо порядковим номером від
одиниці до 20. Потім впорядковуємо кожну
пояснювальну змінну та залишки,
посортувавши їх від меншого до більшого
(Exel, меню «Данные», розділ «Сортировка»).
У результаті порядковий номер чисел
цих показників зміниться і характеризуватиме
ранг його в масиві.
Запишемо ранги пояснювальних змінних та ранг залишків у табл. 7.8.
4. Знайдемо різниці між рангами j-ї змінної та залишками, отриманими на основі цієї змінної, піднесемо їх до квадрата (табл. 7.9).
|
|
|
16 |
16 |
16 |
25 |
9 |
9 |
1 |
9 |
81 |
4 |
36 |
1 |
1 |
4 |
144 |
36 |
0 |
1 |
1 |
9 |
100 |
1 |
9 |
36 |
1 |
100 |
36 |
121 |
9 |
121 |
64 |
36 |
81 |
4 |
9 |
1 |
9 |
9 |
9 |
16 |
1 |
49 |
36 |
4 |
16 |
0 |
16 |
169 |
0 |
4 |
36 |
25 |
225 |
36 |
25 |
0 |
169 |
196 |
169 |
9 |
|
|
|
5. Визначимо коефіцієнти рангової кореляції (простий мішаний момент):
 ;
;
 ;
;
 .
.
6. Розрахуємо t-критерії для визначення статистичної значущості коефіцієнтів рангової кореляції Спірмена за формулою:
 ;
;
 ;
;
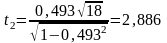 ;
;
 .
.
Критичне
значення t-критерію
для = 0,05
і ступенів свободи n – 2 = 18
дорівнює:
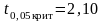 .
.
Порівнюючи
розраховані t-критерії
з критичним значенням, робимо висновок,
що коефіцієнти рангової кореляції
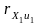 та
та
 є статистично значущими. Звідси можна
зробити висновок, що пояснювальні
змінні Х1
та Х2
можуть викликати гетероскедастичність.
є статистично значущими. Звідси можна
зробити висновок, що пояснювальні
змінні Х1
та Х2
можуть викликати гетероскедастичність.
7.3.6. Тест Парка. Для визначення наявності гетероскедастичності у статистичній інформації Р. Парк запропонував параметричний тест, в основі якого лежить визначення кількісної залежності між дисперсією пояснювальної змінної, яка може викликати гетероскедастичність, та значеннями цієї змінної за функцією:
 ,
(7.9)
,
(7.9)
де
 — дисперсія
j-ї
пояснювальної змінної;
— дисперсія
j-ї
пояснювальної змінної;
— дисперсія залишків;
 — i-те
значення j-ї
пояснювальної змінної;
— i-те
значення j-ї
пояснювальної змінної;
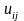 — стохастичні
залишки для i-го
спостереження j-ї
пояснювальної змінної.
— стохастичні
залишки для i-го
спостереження j-ї
пояснювальної змінної.
Прологарифмувавши вираз, дістанемо:
 ,
,
де вираз vj ln(uj) замінено на vj.
Оскільки , як правило, невідомі, то Парк запропонував замінити їх квадратами залишків.
Розглянемо алгоритм тесту Парка.
Крок 1. Побудова рівняння регресії між змінною (Y) та відповідною пояснювальною змінною (Xj)
 .
.
Крок
2.
Визначення залишків
 та піднесення їх до квадрата
та піднесення їх до квадрата
 .
.
Крок
3.
Знаходження логарифмів
 та
.
та
.
Крок 4. Побудова рівняння регресії
 ;
(7.10)
;
(7.10)
де
 .
.
Якщо досліджуються кілька пояснювальних змінних, то таке рівняння регресії будується для кожної з них.
Крок
5.
Перевірка
статичної значущості оцінки параметра
 на основі t-критерію
на основі t-критерію
 .
Якщо фактичне значення t-статистики
більше за критичне значення t-критерію,
для вибраного рівня значущості
і ступеня свободи n – 2,
то
.
Якщо фактичне значення t-статистики
більше за критичне значення t-критерію,
для вибраного рівня значущості
і ступеня свободи n – 2,
то
 є статистично значущий. А це означає,
що гіпотезу про наявність
гетероскедастичності, що викликається
Xj,
не можна відхиляти. Зауважимо, що тест
Парка не вичерпує проблему визначення
гетероскедастичності, бо вона може
існувати навіть якщо врахувати ті
пояснювальні змінні, які в даному
випадку не досліджуються, але вони
впливають на залежну змінну. Тому поряд
із цим тестом доцільно використовувати
інші. Зокрема, тест Глейзера доповнює
тест Парка аналізом гетероскедастичності,
що викликається тими змінними, які не
включено до економетричної моделі. Він
може виявити наявність мішаної
гетероскедастичності.
є статистично значущий. А це означає,
що гіпотезу про наявність
гетероскедастичності, що викликається
Xj,
не можна відхиляти. Зауважимо, що тест
Парка не вичерпує проблему визначення
гетероскедастичності, бо вона може
існувати навіть якщо врахувати ті
пояснювальні змінні, які в даному
випадку не досліджуються, але вони
впливають на залежну змінну. Тому поряд
із цим тестом доцільно використовувати
інші. Зокрема, тест Глейзера доповнює
тест Парка аналізом гетероскедастичності,
що викликається тими змінними, які не
включено до економетричної моделі. Він
може виявити наявність мішаної
гетероскедастичності.
Приклад 7.6. Необхідно перевірити наявність гетероскедастичності у статистичній інформації, наведеній у табл. 4.2 (приклад 7.2), використавши параметричний тест Парка.
Розв’язання
1. Побудуємо прості економетричні моделі, які описують зв’язок залежної змінної з кожною з пояснювальних.
2. Визначимо залишки за кожною з моделей та піднесемо їх до квадрата:
|
|
|
7,803728 |
2,12766 |
0,228826 |
7,114145 |
5,119856 |
3,128598 |
0,449769 |
4,905264 |
3,283594 |
5,252388 |
9,809945 |
16,47719 |
4,689516 |
4,271538 |
11,3932 |
94,18272 |
108,3832 |
31,05978 |
16,31553 |
33,70402 |
28,61863 |
3,204467 |
8,620936 |
5,642439 |
3,659451 |
13,50481 |
3,766662 |
1,991663 |
2,590736 |
0,984613 |
4,674746 |
3,028306 |
13,25007 |
0,081215 |
0,229393 |
21,62587 |
3,85794 |
0,271494 |
0,865814 |
50,226 |
0,424683 |
1,143849 |
1,189067 |
0,343823 |
3,628063 |
0,115322 |
0,207696 |
6,700729 |
2,534942 |
2,948057 |
40,44878 |
0,220227 |
4,41369 |
3,165133 |
0,163569 |
3,659304 |
0,647745 |
0,120004 |
23,49939 |
2,216094 |
3. Прологарифмуємо квадрати залишків та пояснювальні змінні і подамо їх у табл 7.10.
Таблиця 7.10
Побудуємо
три економетричні моделі такого виду:
 ;
де
;
де
 .
.
1)
 ;
;
2)
 ;
;
3)
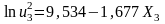 .
.
4. Розрахуємо t-критерії для перевірки статистичної значущості кожної з оцінок параметрів цих моделей:
а) для першої моделі:


б) для другої моделі:


в) для третьої моделі:


5.
Порівнюючи кожний із фактичних
t-критеріїв
із табличним, робимо висновки, що
гетероскедастичність в досліджуваній
статистичній інформації може існувати
за рахунок кожного з чинників, бо
 .
.
 =
2,10т для
і ступенів свободи
=
2,10т для
і ступенів свободи

=
1,77 для
 і ступенів свободи
і ступенів свободи

Зауважимо, що висновки про наявність гетероскедастичності на основі декількох тестів не завжди збігаються. Це пов’язано з тим, що кожний із них побудований за певних вихідних припущень, тобто має свої переваги та недоліки. На наш погляд, тест Глейзера є найбільш простий і одночасно найбільш точний. Хоч і в даному випадку може бути присутня помилка специфікації рівняння регресії залишків від пояснювальної змінної.









