§ 4. Задача о поршне.

В газовой динамике подвижную непроницаемую для частиц среды поверхность принято называть поршнем.

Граничное условие, которому удовлетворяет скорость газа на поршне в случае одномерных течений, имеет вид

(4.1)

где x_П - координата поршня.

Рассмотрим следующую задачу. Пусть полупространство x>0 занято однородным покоящимся газом. Его параметры помечаем индексом 0: p₀ , ρ₀ , a₀ , v₀=0. Например, это может быть газ в полубесконечной цилиндрической трубе, ось которой направлена по координатной оси x, ограниченный непроницаемой плоской поверхностью (поршнем) x=0. Предположим, что, начиная с момента t=0 , поршень приходит в движение с нулевой начальной скоростью (случай рассмотрим позже).

Тогда звуковая характеристика ОА : x=a₀t будет отделять невозмущенный газ от возмущенного (рис. ). По теореме о примыкании, течение в окрестности этой характеристики слева от нее представляет собой простую волну. Вплоть до момента градиентной катастрофы (если таковая возникает) либо на всем полубесконечном интервале времени 0<t<∞ (если движение остается непрерывным) удельная энтропия s и инвариант l сохраняют свои значения постоянными:

s(t;x)≡s₀ , l(t;x)≡l₀ . (4.2)

Действительно, изоэнтропичность рассматриваемого течения следует из его адиабатичности и непрерывности, а также из однородности распределения энтропии по частницам в начальный момент времени, а постоянство инварианта l во всем потоке – из равенства значений l на всех C_-- характеристиках, которые приходят в область плоскости (x;t), “занятую” возмущенным газом, из области, отвечающей невозмущенному однородному состоянию.

Пусть скорость поршня во все время движения переменна. Тогда течением в виде простой волны, распространяющейся по газу вправо, будет занята вся часть OAB плоскости (x;t), находящаяся между траекторией поршня OB и передним фронтом возмущения OA (рис. ).

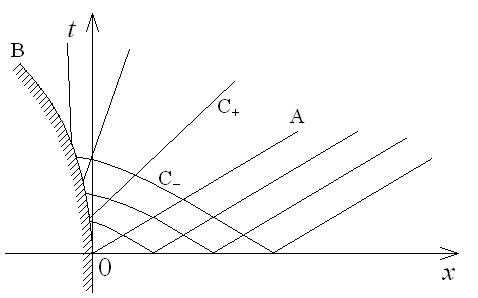
Заметим, что траектория OB поршня является C₀ - характеристикой (в силу условия равенства скорости поршня и скорости частиц газа, контактирующих с поршнем). Именно поэтому характеристики семейства С₊ уходят от поршня (с ростом времени t ), а характеристики семейства C_- приходят к поршню.

Пусть закон движения поршня x_П(t) задан, то есть известно уравнение линии OB . Для удобства ограничимся рассмотрением случая совершенного газа с показателем адиабаты γ .

Обозначим u скорость поршня (точнее, ее проекцию на ось x ). Из равенств можно выразить t и x_П в виде функций от u: t=t(u), x_П=x_П(t) . Подставляя эти выражения во второе равенство (3.2), выразив предварительно a через v из первого равенства (3.2), которое в данном случае имеет вид

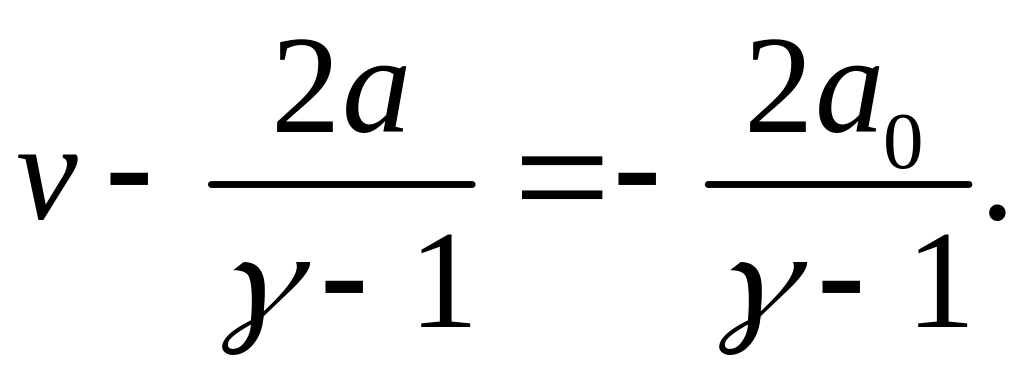(4.3)

В результате получим

где .

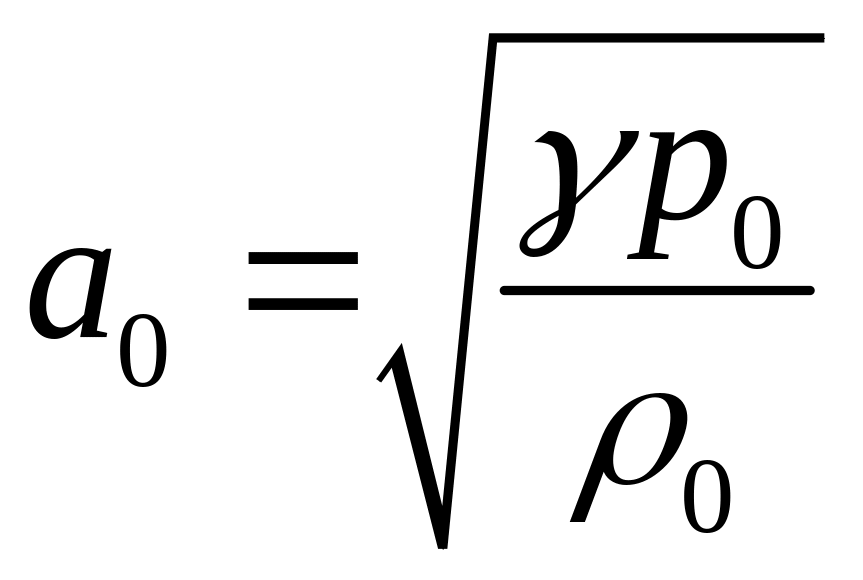Знание зависимости f(u) (или, что то же самое, f(v) ) позволяет полностью описать течение возмущенного газа в виде волны Римана (см. §3).

Таким образом решается задача о поршне для случая, когда возникающее движение газа не содержит сильных разрывов (ударных волн). Если разрывы все же возникают, то полученное решение годится на интервале времени от начала движения поршня до момента наступления первой градиентной катастрофы.

Когда поршень выдвигается из газа достаточно быстро, возможным становится отрыв частиц газа от поршня. Нетрудно заметить, что модуль направленной влево скорости частиц не может превышать значения

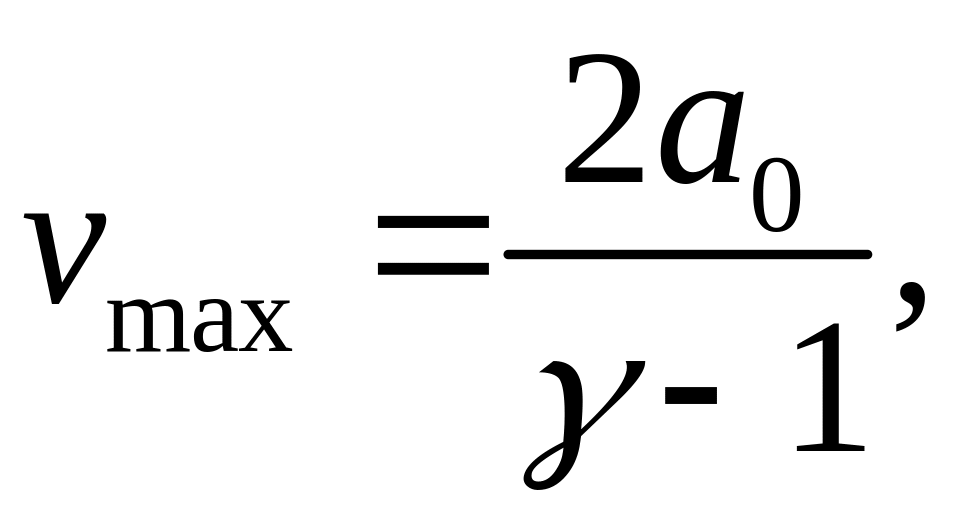(4.4)

поскольку в равенстве (4.3) скорость звука a не может быть отрицательной. Величина (4.4) называется скоростью нестационарного истечения газа в вакуум. На границе газ-вакуум давление, плотность и скорость звука (при адиабатическом движении) обращаются в нуль. Если поршень выдвигается со скоростью большей, чем v_max , то между ним и областью, занятой газом, образуется зона вакуума.

В предельном случае, когда поршень с самого начала движения имеет скорость, большую, чем v_max , направленную влево, газ будет двигаться точно так же, как если бы в момент t=0 мгновенно исчезла перегородка, отделяющая полупространство x>0 , занятое однородным покоящимся газом, от полупространства x<0 , в котором газ отсутствует. Возникающее течение представляет собой центрированную простую волну и описывается формулами (3.3), в которых следует положить l₀=-2a₀/(γ-1) . Такое течение естественно называть нестационарным истечением газа в вакуум. Область, занятая в момент t движущимся газом, определяется условием

а зависимости скорости частиц и скорости звука от t , x имеют вид

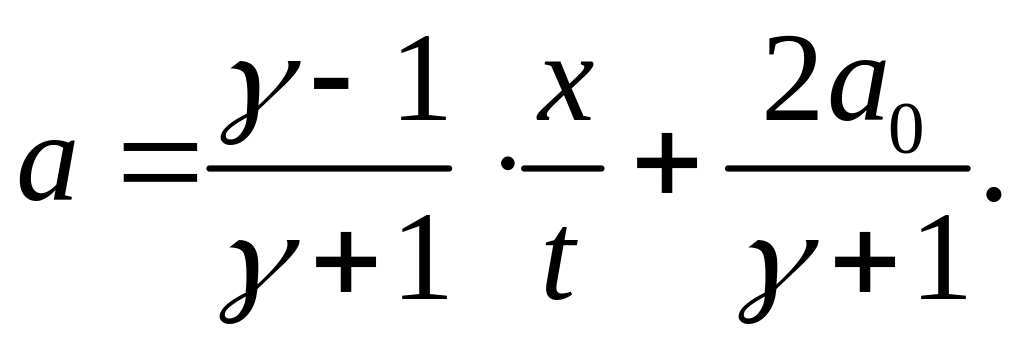(4.5)

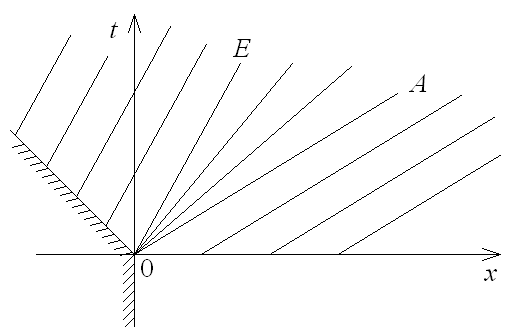
Формулами (4.5) описывается центрированная простая волна в задаче о поршне, выдвигающемся с постоянной скоростью из трубы с газом. Причем задний фронт центрированной волны Римана распространяется со скоростью . В плоскости (x; t) ему отвечает C₊-характеристика OE (рис. ).

Течение между этим фронтом и поршнем представляет собой однородный поток, скорость в котором равна скорости поршня (область BOE на рис. ).

Перейдем теперь к случаю движения поршня в сторону области, занятой покоящимся газом. Возникающая здесь простая волна является волной сжатия, поэтому в какой-то момент времени обязательно произойдет градиентная катастрофа. Эта катастрофа, сопровождающаяся появлением ударной волны, может наступить и в начальный момент t=0, если поршень приходит в движение с ненулевой начальной скоростью.

Начнем с рассмотрения последнего случая. Пусть скорость поршня постоянна: при t>0 . Данная задача допускает решение, в котором невозмущенный газ отделен от движущегося ударной волной, интенсивность которой не зависит от времени и определяется скоростью поршня. (Доказательство единственности этого решения см., например, в [Овсянников, с. 206, § 18]). Весь газ, находящийся за фронтом ударной волны движется с одной и той же постоянной скоростью – скоростью поршня (рис.___).

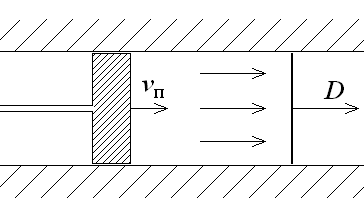
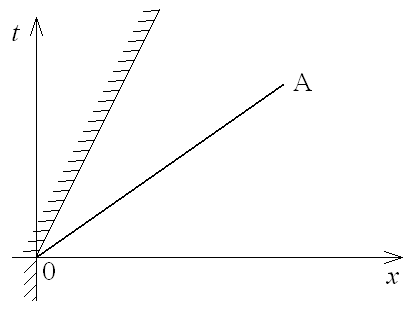
Определим параметры возмущенного газа по заданным значениям ρ₀ , p₀ , γ и скорости поршня v_П . Для этого воспользуемся условиями на ударной волне, выражающими непрерывность плотности потока массы, импульса и энергии через поверхность сильного разрыва [Седов I; Черный; Овсянников; Ландау, Лифшиц].

В подвижной системе отсчета, связанной с поверхностью разрыва, указанные условия записываются в виде

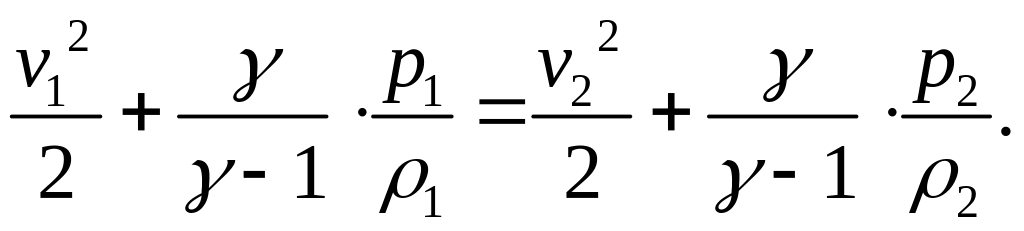
Здесь ρ_i , v_i , p_i ( i=1,2 ) – предельные значения плотности, скорости и давления газа при подходе к поверхности разрыва с одной и другой стороны.

В неподвижной системе отсчета, обозначая скорость фронта ударной волны D , будем иметь

(4.6)

где ρ , p и v=v_П - плотность, давление и скорость газа, находящегося между поршнем и ударной волной.

Из первого равенства получаем

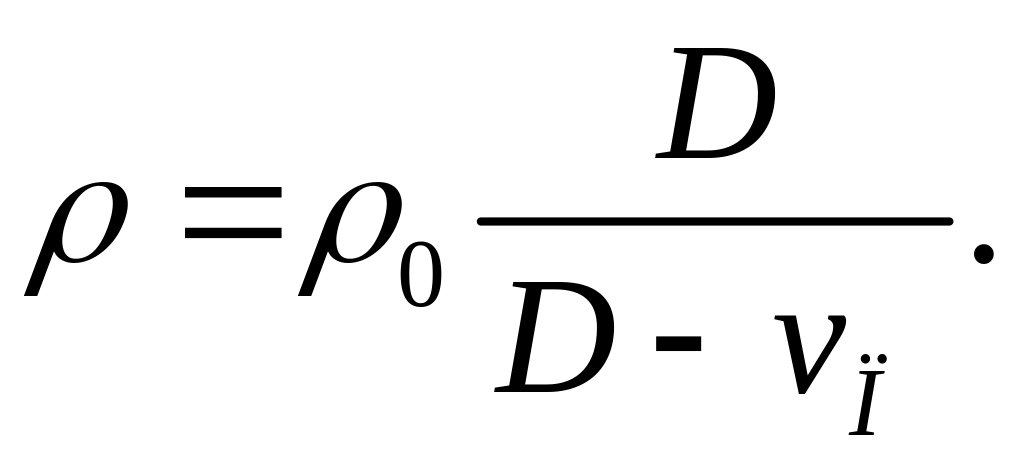(4.7)

Второе равенство с учетом первого приводит к соотношению

(4.8)

Тогда последнее условие (4.6) приобретает вид квадратного уравнения относительно D :

Решая его (учитывая, что и ), получим

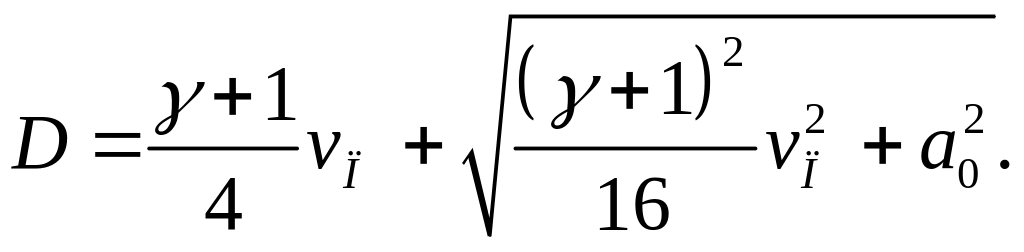(4.9)

Подставляя данное выражение D в (4.7), (4.8), найдем зависимости для плотности и давления сжатого ударной волной газа от скорости поршня.

В предельном случае v_П >> a₀ быстро выдвигающегося поршня скорость ударной волны оказывается прямо пропорциональной скорости поршня: Тогда из (4.7) получим 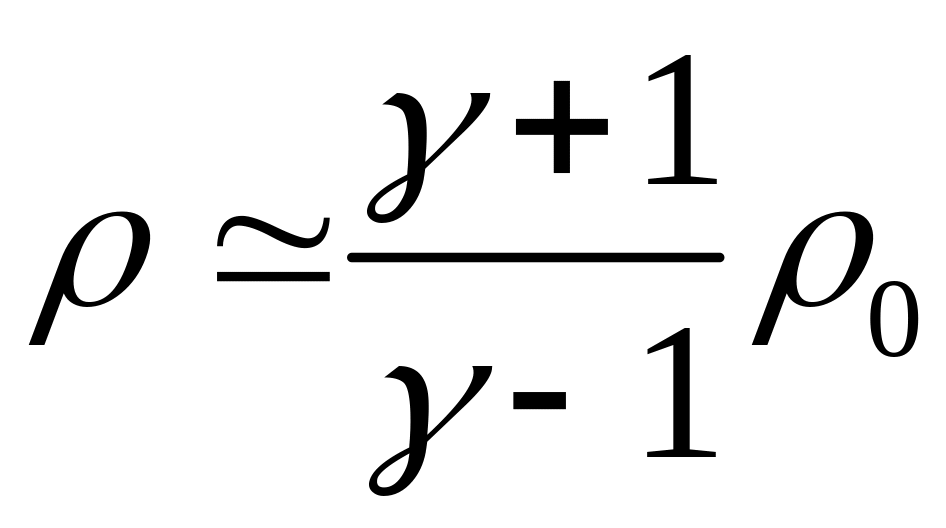, что, как известно, соответствует максимально возможной степени сжатия газа в ударной волне.

В другом предельном случае v_П << a₀ скорость ударной волны приблизительно равна скорости звука: D ≈ a₀ . Этот вывод вполне очевиден, если учесть, что слабые возмущения распространяются по сжимаемой среде как раз со скоростью звука. Менее очевидной представляется оценка для скачка давления в слабой ударной волне. Из (4.8) получаем

(4.10)

Тогда, например, для воды, в которой при нормальных условиях скорость звука – около 1400 м/с, а плотность массы – 1000 кг/м³_, при скорости поршня 1 м/с скачок давления составляет ∆p ≈ 1,4∙10⁶ Па, что примерно в 14 раз больше атмосферного давления. Такое явление носит название гидравлического удара и наблюдается при резком закрывании (или неисправности) запорных устройств в водопроводных сетях или в трубопроводах. Внезапно появляющаяся на пути потока жидкости в трубе преграда «превращается» во вдвигающийся поршень, если систему отсчета связать с движущейся жидкостью. В некоторых случаях гидравлический удар приводит к разрыву трубопроводов.