31

ВВЕДЕНИЕ

Газовая динамика изучает быстропротекающие процессы в сжимаемых средах. Для описания таких процессов очень часто используется математическая модель идеального (невязкого) газа, при условии, что решающую роль в исследуемых явлениях играет свойство сжимаемости, а диссипативными эффектами (вязкостью, теплопроводностью) можно пренебречь.

Круг явлений, поддающихся изучению методами газовой динамики достаточно широк. Перечислим некоторые из них:

- обтекание воздухом движущихся с большой скоростью тел: самолетов, снарядов, ракет;

- явления взрыва и сопровождающие их процессы распространения и взаимодействия ударных волн;

- высокоскоростные течения газов в технических устройствах – реактивных двигателях, газовых турбинах и компрессорах;

- различные процессы в атмосферах планет и звезд, а также в межзвездной среде.

Наиболее полно изучены в газовой динамике одномерные нестационарные и двумерные установившиеся движения. Для них известно много точных (аналитических) решений. Математический аппарат газовой динамики лучше всего развит применительно именно к таким течениям.

Аналитические, приближенные и численные методы газовой динамики находят продолжение и развитие в других разделах механики сплошных сред.

§ 1. Уравнения одномерных нестационарных движений идеального газа. Характеристики. Переменные Римана.

Используя в качестве независимых переменных время и эйлерову координату , являющуюся одной из координат прямоугольной декартовой системы в случае движения с плоскими волнами или равную расстоянию от центра или оси симметрии в случае движений со сферическими или цилиндрическими волнами, запишем дифференциальные уравнения одномерных нестационарных движений газа в виде

(1.1)

(1.2)

(1.3)

(1.4)

Здесь – плотность, – скорость (точнее, ее единственная ненулевая составляющая – проекция на ось ), – давление, – энтропия единицы массы газа, ν – параметр, характеризующий геометрию течения и принимающий значения 1, 2, 3 в случае движений с плоскими, цилиндрическими и сферическими волнами соответственно. Уравнение (1.3) выражает условие адиабатичности изучаемых движений, а (1.4) – тот факт, что газ рассматривается как двухпараметрическая среда.

В частном случае совершенного газа с постоянными теплоемкостями C_V, C_P энтропия может быть представлена в виде , где - показатель адиабаты Пуассона. Тогда соотношения (1.3), (1.4) заменяются одним уравнением: . Для реальных газов используют также эмпирические зависимости давления от плотности и энтропии вида , где - постоянная величина. В случае , процесс называется политропным, а показатель степени называется показателем политропы.

Отметим также, что при изучении волн давления в жидкостях часто пользуются уравнением состояния в форме Тэта: Например, для воды полагают , а считают постоянной.

Заменяя в уравнении (1.2) производную выражением , перепишем его в виде

(1.5)

Здесь и - это частные производные функции, стоящей в правой части равенства (1.4).

Систему уравнений (1.1), (1.3), (1.5) запишем в матричной форме:

(1.6)

где

Данная система представляет собой нормальную форму системы квазилинейных уравнений в частных производных первого порядка относительно трех функций

Собственные значения матрицы А определяются из характеристического уравнения или

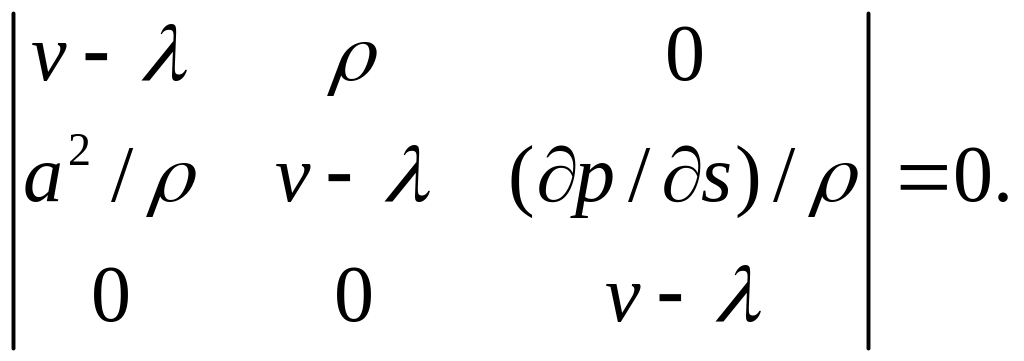(1.7)

Раскрывая определитель, получаем

откуда сразу находим

. (1.8)

Умножим обе части равенства (1.6) на левый собственный вектор-строку , отвечающий собственному значению

Поскольку, по определению левого собственного вектора , то из последнего равенства получим

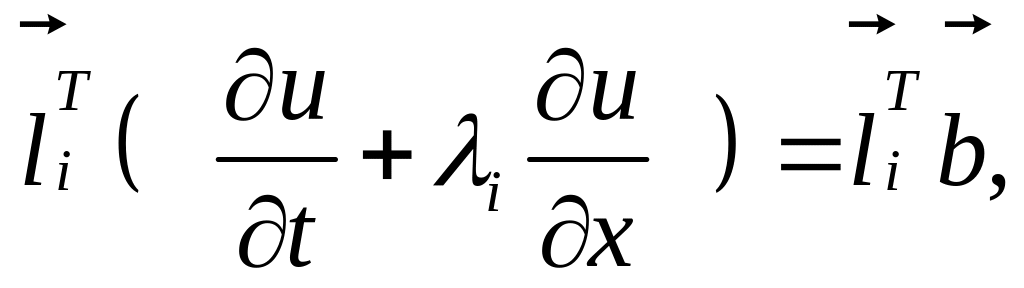
(1.9)

В рассматриваемом случае три собственных вектора отвечают различным собственным значениям, а потому образуют линейно независимую систему векторов. Это означает, что система уравнений (1.9) эквивалентна исходной системе (1.6).

Замечательной особенностью уравнений (1.9) является то, что в каждом из них участвуют производные только по одному направлению в плоскости . Действительно, при фиксированном значении индекса i , выражение

представляет собой производную вектор-функции по переменной t в направлении

(1.10)

Если система квазилинейных уравнений в частных производных первого порядка относительно функций двух независимых переменных может быть приведена к такому виду, где каждое уравнение содержит производные только по какому-то одному направлению, то эта система называется гиперболической, а соответствующие направления – характеристическими. Интегральные кривые (векторные линии) поля характеристических направлений называются характеристиками рассматриваемой гиперболической системы уравнений.

Как показано выше, уравнения одномерных нестационарных движений идеального газа образуют гиперболическую систему.

Левые собственные векторы, отвечающие собственным значениям (1.8) матрицы A из (1.6), имеют вид

(1.11)

Подставляя (1.11) в (1.9), получаем характеристическую форму дифференциальных уравнений (1.6) одномерных нестационарных движений газа:

(1.12)

Учитывая тождество

эту систему можно переписать также в виде

(1.13)

Умножив правые и левые части равенств (1.13) на dt , представим их как уравнения в дифференциалaх:

при (1.14)

при

при

Таким образом, через каждую точку плоскости (t; x) проходят три характеристики. Энтропийные (контактные) характеристики описываются уравнением и совпадают с траекториями частиц газа в плоскости (t; x); звуковые (акустические) характеристики описываются уравнением либо . В дальнейшем для краткости будем называть эти характеристики соответственно C₀ - , C₊ - и C_- - характеристиками.

Отметим, что каждому решению уравнений газовой динамики (1.6) отвечает своя сетка характеристик в плоскости (t; x) , поскольку характеристические скорости зависят от .

Рассмотрим частный случай – баротропное движение газа, когда давление представляется в виде функции только плотности: . Этот случай отвечает, например, изоэнтропическому течению, в котором и .

Тогда уравнение для энтропии использовать не нужно, а второе и третье равенства из системы (1.14) можно представить в виде

(1.15)

где

(1.16)

В дальнейшем (предполагая ) будем считать функцией скорости звука : . Введя обозначения , для величин, называемых правой и левой переменными Римана, получаем характеристическую форму уравнений одномерных нестационарных движений газа в переменных Римана:

(1.17)

Роли «неизвестных» функций здесь играют и , а скорость v частиц газа и скорость звука a через них выражаются:

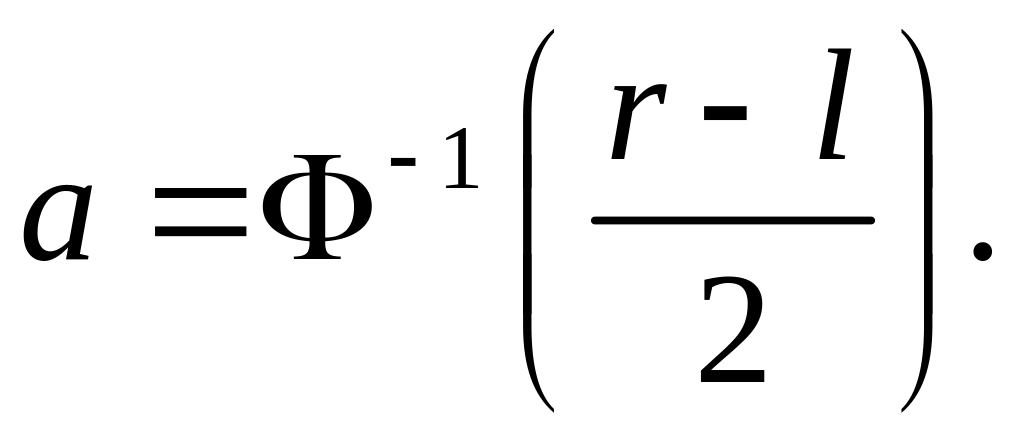(1.18)

Для изоэнтропического движения совершенного газа с постоянными теплоемкостями имеем

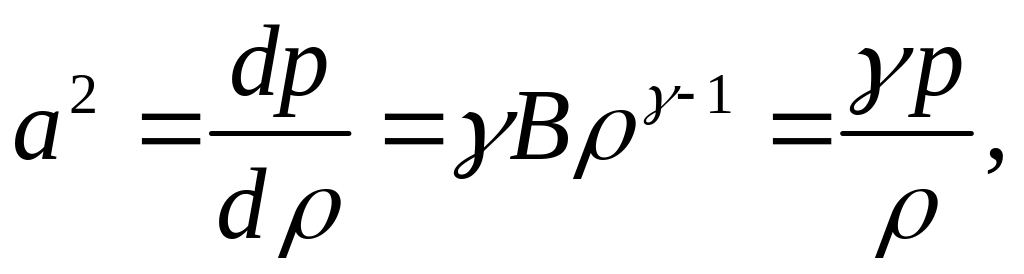
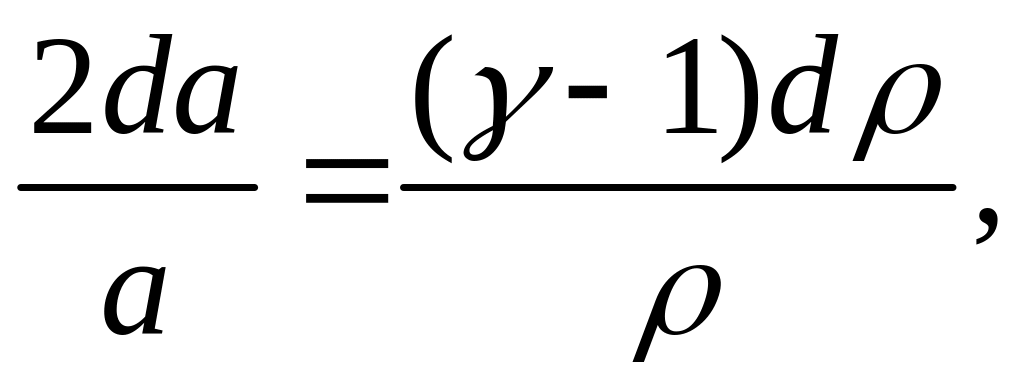
Выбирая аддитивную постоянную , получаем

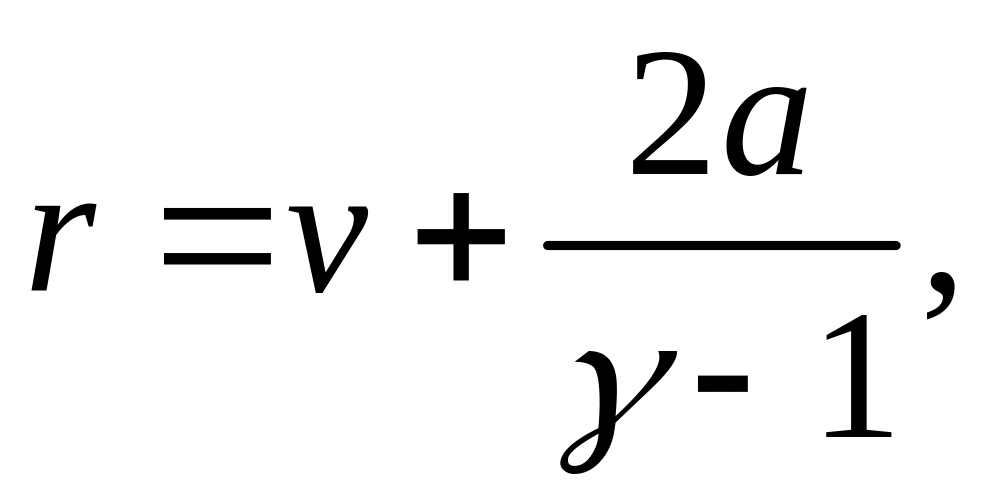
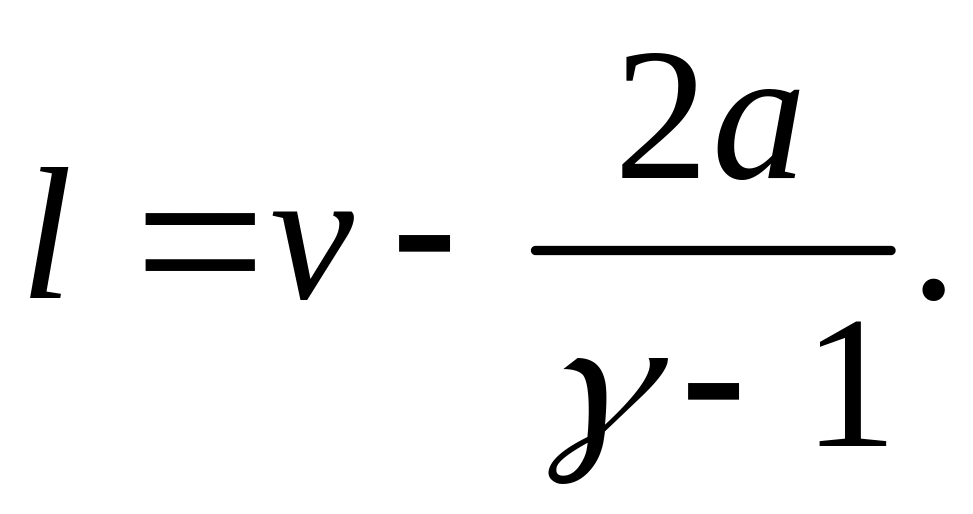(1.19)

Если рассматриваются одномерные бaротропные течения газа с плоскими волнами ( ), то правые части уравнений (1.17) обращаются в нуль. Это означает, что в данном случае величины r и l постоянны на C₊- и на C_-- характеристиках соответственно. Поэтому их называют также инвариантами Римана.

Пусть имеется некоторое решение уравнений одномерных нестационарных движений газа с плоскими волнами, в котором значение энтропии s постоянно. Рассмотрим другое, «возмущенное» решение, отличающееся от заданного в начальный момент t₀ на некотором конечном интервале оси x . Тогда, в соответствии с вышесказанным, возмущения инварианта r будут переноситься по частицам вдоль C₊ - характеристик (т.е. со скоростью звука - вправо), а возмущения инварианта l будут переноситься вдоль C_- - характеристик (т.е. со скоростью звука - влево). Это означает, что интервал оси x , на котором два рассматриваемых решения различаются, с течением времени расширяется одновременно влево и вправо со скоростью звука (относительно частиц газа).

Заметим, что данный вывод справедлив лишь для непрерывных движений. В разрывных решениях уравнений газовой динамики, содержащих ударные волны, т.е. скачкообразные возмущения параметров газа, эти возмущения распространяются по частицам со сверхзвуковой скоростью (см. §4).