4.4 Закон Ньютона-Рихмана. Коэффициент теплоотдачи – физический смысл
В процессе конвективного переноса теплоты характер течения жидкости имеет очень большое значение, так как им определяется механизм теплоотдачи. Процесс теплопереноса на границе твердой стенки может быть выражен законом Фурье:
,
(4.5)
где n – нормаль к поверхности стенки.
Это же количество теплоты, переданное в процессе конвективного теплообмена, определяется по закону Ньютона-Рихмана:
dQ = α·(tст. – tж) · dF. (4.6)
Приравнивая эти уравнения получим:
или:
(4.7)
Последнее дифференциальное уравнение описывает процесс теплообмена на поверхности стенки при n = 0.
Конвективный теплообмен является весьма сложным процессом и зависит от большого числа факторов, определяющих процесс теплоотдачи.
Интенсивность этого процесса характеризуется коэффициентом теплоотдачи α:
(4.8)
Коэффициент теплоотдачи – это количество теплоты, отдаваемое в единицу времени единицей поверхности, при разности температур между поверхностью и жидкостью в один градус.
В общем случае коэффициент теплоотдачи α является функцией теплофизических параметров жидкости (λ, с, ρ, α, μ), характера течения жидкости (Х – свободное или вынужденное), скорости движения жидкости (w), температурного напора (Δt), формы и размеров тела (Ф, l1, l2, l3) и др.
α = f(λ, с, ρ, α, μ, Х, w, tст., tж, Δt, Ф, l1, l2, l3 и др.); (4.9)
Коэффициент теплоотдачи величина сложная и для ее определения невозможно дать общую формулу.
4.5 Дифференциальные уравнения конвективного теплообмена – математическая модель переноса теплоты конвекцией
На основе общих законов физики составлены дифференциальные уравнения для всего класса явлений конвективного теплообмена, учитывающие как тепловые, так и динамические явления в любом процессе.
1. Дифференциальное уравнение энергии – устанавливает связь между пространственным и временным изменением температуры в любой точке движущейся жидкости:
(4.10)
Если wх = 0, wу = 0, wz = 0, т.е. жидкость не движется, уравнение энергии переходит в уравнение теплопроводности без внутренних источников теплоты.
2. Дифференциальное уравнение теплообмена – характеризует условия теплообмена на границе твердого тела и жидкости:
(4.11)
3. Дифференциальное уравнение движения вязкой несжимаемой жидкости, уравнение Навье-Стокса:
для оси х:
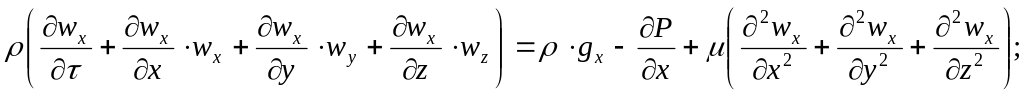
для оси у:
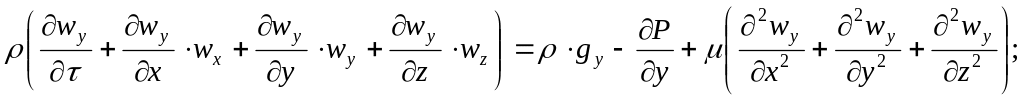(4.12)
для оси z:
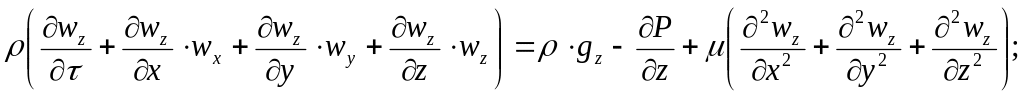
Это уравнение справедливо для ламинарного и турбулентного движений, причем для турбулентного движения w – действительная (мгновенная) скорость, равная сумме средней и пульсационной скоростей.
4. Дифференциальное уравнение сплошности – уравнение непрерывности потока.
Для сжимаемых жидкостей:
(4.13)
Для несжимаемых жидкостей при ρ = const:
(4.14)
Эта система уравнений является математической моделью всего класса явлений конвективного теплообмена, как при свободном, так и при вынужденном движении.
Для определения конкретного явления или группы явлений к этой системе необходимо добавить условия однозначности.
И при добавлении условий однозначности система уравнений, как правило, не имеет решений. Поэтому прибегают к помощи теории подобия, экспериментальным исследованиям и теории размерностей – и составляют критериальные уравнения (в безразмерном виде) для определенной группы явлений.