2.4. Расширенный фильтр Калмана

В случае параметрической неопределенности модели сигнала образуем расширенный вектор состояния , включив в него наряду с исходным вектором состоянияY вектор неизвестных параметров . Уравнение динамической системы (2.6) представим в виде

Y_k+1 = Ф_k()Y_k + U_k() +W_k. (2.19)

Считая неизвестные параметры постоянными во времени, дополним модель динамической системы (2.1) уравнением _k+1 = _k. Тогда для расширенного вектора состояния имеем уравнение состояния X _k+1 = f [X_k , U_k ] + W _k.

Это уравнение нелинейно (исключение составляет случай, когда от  зависит лишь член U_k() в (2.19) и эта зависимость линейна). В общем случае решение задачи нелинейной фильтрации достаточно сложно. Часто приемлемое приближенное решение можно получить, используя так называемые линеаризованные фильтры [2, c. 51-56]. В работе используется расширенный фильтр Калмана, (линеаризованный фильтр, в котором линеаризация на каждом шаге производится в точке текущей оценки ). Уравнения этого фильтра отличаются от уравнений (2.8) - (2.14), помимо очевидной замены обозначений (X вместо Y), следующим:

1) уравнение экстраполяции оценки заменяется на уравнение

,

2) в уравнении экстраполяции ковариационной матрицы ошибки оценки матрица Ф_k заменяется на матрицу где

.

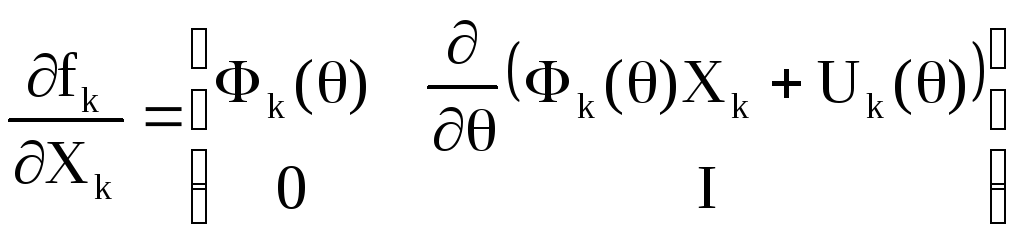Отметим, что в некоторых случаях ошибки линеаризации могут существенно влиять на качество получаемых оценок и даже вызывать расходимость фильтра. Устранение этого нежелательного эффекта достигается с помощью введения параметра старения данных.

5. Алгоритм адаптивной фильтрации

Пусть на интервале времени от T₁ до T₂ появляется импульсное входное воздействие U_k, неучтенное в модели сигнала. Моменты T₁, T₂ и форма U_k считаются неизвестными. В этом случае в стандартном фильтре Калмана при t_k > T₁ будет наблюдаться ярко выраженный эффект расходимости. Обеспечить устойчивость процедуры фильтрации можно, применив так называемые адаптивные методы. С алгоритмами адаптивной фильтрации можно ознакомиться в [2, c. 68-73]. В настоящей лабораторной работе применен адаптивный фильтр, в котором обнаружение расходимости производится на основе сравнения теоретической и фактической дисперсий невязок измерений. При этом фактическая дисперсия аппроксимируется выборочной оценкойпо последним М измерениям, включаяz_k. В нормальном режиме работы фильтра проверяется соотношение . Фильтр переводится в режим устранения расходимости, как только обнаруживается выполнение неравенства. После этого включается механизм подавления расходимости, использующий для загрубления модели сигнала эффектстарения данных, описанный в 2.3. Однако здесь на каждом шаге оценивания параметр старения подбирается адаптивно (так, чтобы обеспечить соответствие):.

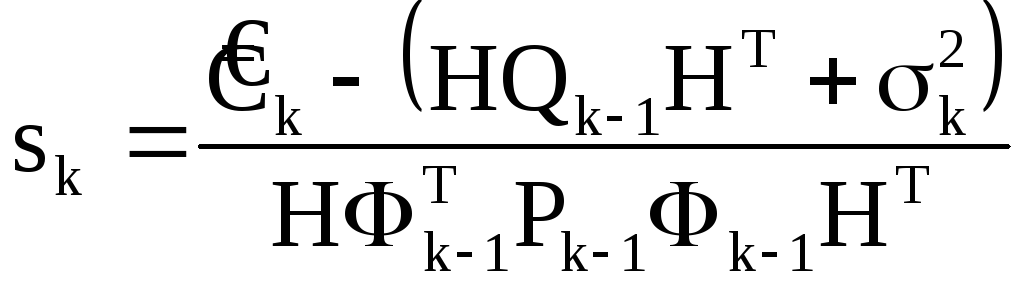В режиме устранения расходимости проверяется неравенство . Как только это неравенство перестает выполняться, считается, что расходимость устранена, после чего отключается механизм подавления расходимости и фильтр продолжает работу в нормальном режиме. Параметрами описанного адаптивного фильтра являются величиныM, , .