1.5. Контрольные вопросы

1. Почему рассмотренный в этой лабораторной работе метод оценивания называется МНК?

2. Почему модели сигнала (1.14) и (1.15) называются линейными, а модель (1.16) - нелинейной?

3. Каков содержательный смысл и размерность величин , h_k, K_k, Q_k, P_k, Q_k-1, H_k в соотношениях (1.6 - 1.13)?

4. Какие недостатки и достоинства имеют алгоритмы (1.5) и (1.6) - (1.8)? Какой из этих алгоритмов формально более точный?

5. Какими свойствами обладают оценки метода наименьших квадратов и при каких условиях?

6. Каков содержательный смысл условия c  в выражении для начальной ковариационной матрицы Р₀ = cI?

7. В чем состоит явление вычислительной неустойчивости алгоритмов МНК?

8. От чего зависит вычислительная устойчивость алгоритмов МНК?

9. За счет чего достигается повышение вычислительной устойчивости в алгоритмах (1.6), (1.7), (1.10)? Каков содержательный смысл механизма этого явления?

10. Какими свойствами обладают оценки, вычисляемые линеаризованным алгоритмом МНК?

11. Какими способами можно получать начальные условия для рекуррентного алгоритма МНК в линейном и нелинейном случаях?

12. Какие исходные данные необходимы для работы рекуррентного алгоритма МНК?

13. Какие данные получаются на выходе рекуррентного алгоритма?

14. Какова схема машинного эксперимента при исследовании рекуррентных процедур МНК?

15. Какие характеристики анализируются в качестве результатов эксперимента? Как оценивается качество работы алгоритма?

16. Что такое фактическая и теоретическая оценки параметра? Как соотносятся фактическая и теоретическая ошибки оценки параметра сигнала?

17. Каков смысл требования "близости" начальной оценки к вектору Х в нелинейной задаче оценивания и к чему может привести использование грубой начальной оценки?

2. Лабораторная работа № 2 дискретный фильтр калмана

2.1. Постановка задачи фильтрации

Рассматривается задача рекуррентного оценивания состояния линейной динамической системы по результатам наблюдений, выполненных в дискретные моменты времени.

В качестве динамической системы будем рассматривать систему, заданную линейным дифференциальным уравнением вида

, (2.1)

где  (t) - скалярная переменная; m, f и k_f - постоянные параметры; F(t) - заданная функция времени, а W_f(t) - случайный белошумный процесс с M{W_f(t)} = 0 и M{W_f(t)W_f(t)} = (t - t)Q_f(t). Здесь М - символ математического ожидания;  (t – t) – дельта-функция.

Уравнение (2.1) описывает поведение большого класса физических систем, например электрических, механических (поступательное, возратно-поступательное или вращательное движения), акустических, термических, магнитных. Переменные , F, W_f и параметры m, f, k_f в каждой из таких систем имеют свою физическую интерпретацию.

В случае механических систем уравнение (2.1) описывает, например, следующие процессы одномерного движения:

1) при f = 0 и k_f = 0 поступательное движение материальной точки на прямой под действием детерминированных F(t) и (или) случайных W_f(t) возмущений ускорения;

2) при k_f = 0 и W_f(t) = 0 - движение материальной точки на прямой в присутствии силы трения, пропорциональной скорости и под действием заданной внешней силы F(t);

3) при k_f = 0 и F(t) = 0 - движение материальной точки на прямой в вязкой жидкости (f - коэффициент вязкого трения) под действием случайной силы W_f(t) (броуновское движение);

4) при f = 0, k_f > 0 и W_f(t) = 0 - управляемый процесс в одномерной колебательной системе, где входное воздействие заранее известно;

5) при наличии всех членов в (2.1) - линейный осциллятор с трением под действием вынуждающей детерминированной F(t) и случайной W_f(t) силы.

Здесь естественна следующая интерпретация параметров: m - масса; f - коэффициент трения (торможения, вязкости и т. п.); k_f - коэффициент упругости (жесткости).

В случае электрических систем уравнение (2.1), преобразованное для удобства в других обозначениях к виду

описывает, например, управляемый (приложенным напряжением e(t)) процесс в колебательном RLC-контуре под действием случайных возмущений напряжения . Здесьq(t) - заряд; - сила тока;L - индуктивность; C - емкость; R - сопротивление. Уравнение (2.1) можно рассматривать независимо от физической интерпретации как модель случайного процесса (t), который получается линейным преобразованием некоторого исходного случайного процесса W_f(t). Если, например, W_f(t) - белошумный процесс, который, как известно [1], обладает спектральной плотностью a = const, то процесс  (t) будет иметь (см., например, [1]) спектральную плотность

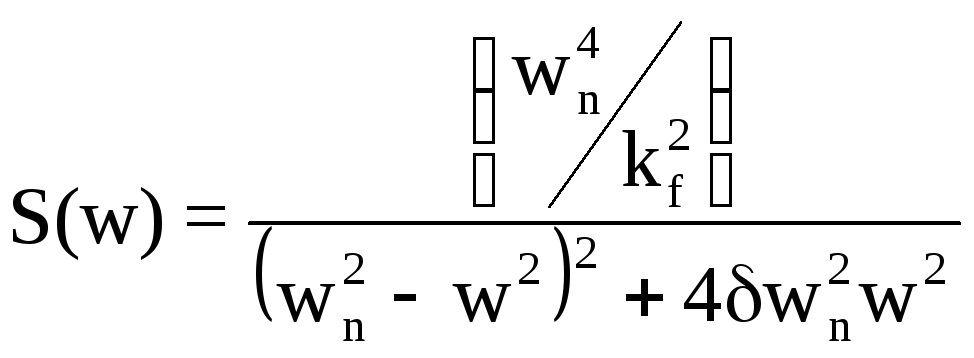
и автокорреляционную функцию

.

Здесь введены обозначения и(для электрической системы -и). Обычно называют w_n - собственной частотой незатухающих колебаний, а  - коэффициентом затухания. 

Пусть над динамической системой (2.1) производится ряд последовательных наблюдений, и по результатам этих наблюдений необходимо в каком-то смысле наилучшим образом определить текущее состояние динамической системы. Причем оценки состояния требуется получать в темпе поступления измерений. Такая задача наиболее естественным образом решается с помощью рекуррентных процедур оценивания. В лабораторной работе будет рассмотрена одна из наиболее известных и широко применяемых процедур такого рода. Речь идет о так называемом фильтре Калмана (ФК).

Задача лабораторной работы состоит в исследовании с помощью машинного эксперимента некоторых свойств процедуры рекуррентной фильтрации на примере оценивания состояния динамической системы вида (2.1).

При решении задач оптимального оценивания состояния динамической системы вида (2.1) удобно перейти к ее описанию с помощью системы линейных дифференциальных уравнений первого порядка. Для этого введем так называемые переменные состояния y₁(t) = (t) и . Тогда уравнение (2.1) можно записать в виде

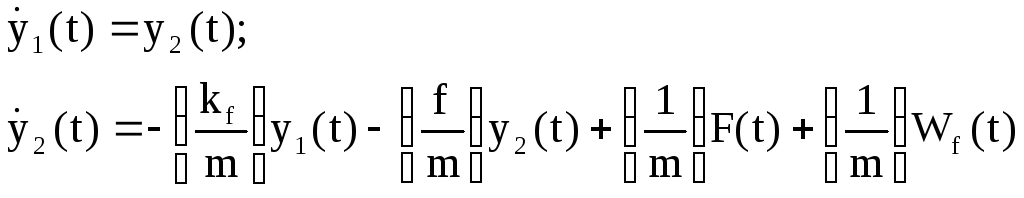
или, вводя вектор состояния Y(t) = (y₁(t) y₂(t))^T, в матричном виде

(2.2)

где матрицы A, B и G имеют вид

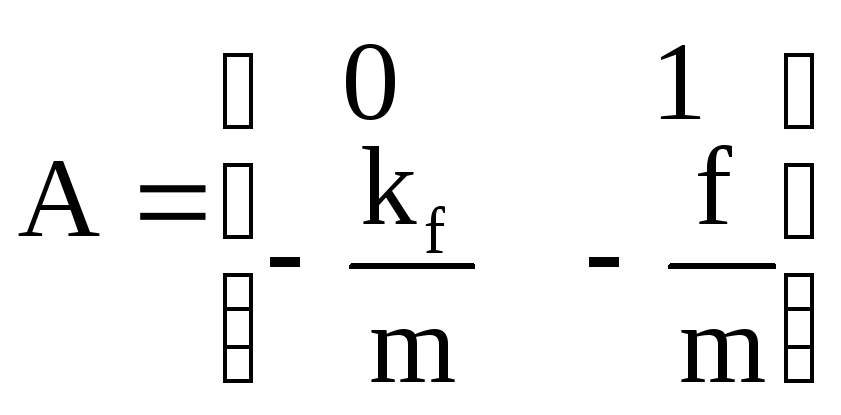; ;(2.3)

и где введены обозначения ,Отметим, что теперь, где

Далее будем предполагать, что в начальный момент времени t₀ известны несмещенная оценка вектора состоянияY(t₀) и ковариационная матрица ошибки этой оценки .

Сформулируем основные предположения относительно процесса наблюдения за динамической системой (1.2). Пусть измеряется только первая компонента вектора состояния на фоне аддитивной помехи. Тогда модель процесса наблюдения запишем в виде

z_k = HY(t_k) + v_k, (2.4)

где H = (1 0), а v_k - случайный процесс, описывающий помеху наблюдения. Свойства процесса v_k задаются его характеристиками M{v_k} = 0 и M{v_k v_j}=_kj . Здесь _kj - символ Кронекера. В дальнейшем, как правило, предполагается, что и возмущения динамической системы , и помеха наблюденияv_k - гауссовские. Кроме того, считаем, что процессы иv_k некоррелированы между собой при любых t и t_k.

Учитывая дискретный во времени характер процесса и результатов наблюдения (2.4), можно при описании динамической системы перейти от дифференциального уравнения (2.2) к конечному разностному уравнению вида

Y_k+1 = Ф_kY_k + U_k + W_k, (2.5)

где Y(t_k) = Y_k, а U_k и W_k - входные воздействия, соответствующие входным воздействиям F(t) и W_f(t) в исходном уравнении (2.1).

Отметим, что теперь в уравнении (2.5) входные воздействия U_k и W_k - векторы, а не скаляры. В дальнейшем в лабораторной работе детерминированная часть входного воздействия F(t) будет для простоты задаваться в виде ступенчатой функции с изменениями в точках t_k, т. е. F(t) = F_k при t  (t_k-1, t_k], где F₁, F₂, …, F_N заданная числовая последовательность.

Далее будем полагать также, что t_k = t_k - t_k-1 =  , где  - постоянная величина для всех k.

Исходной информацией в задаче обработки  являются измерения z₁, z₂, …, z_N и, кроме того, значения параметров модели динамической системы m, F, k_f, q, F(t), априорная информация о состоянии системы в виде начальной оценки и ковариационной матрицы ошибки этой оценкиP₀ = P(t₀), а также параметры "измерителя" _k.

Требуемая выходная информация  представляет собой оценки фильтрации вектора состоянияY_k и характеристики их точности при k = 1, 2, …, N.