8.6. Обобщенные перестановки и сочетания

Рассмотрим теперь разновидность подсчетов, которые представляют собой нечто промежуточное между перестановками и сочетаниями. На самом деле это обоб­щение и того, и другого. Предположим, что требуется определить различные размещения букв в слове миссиссиппи. Проблема состоит в том, что некоторые буквы повторяются. Метод подсчета количества различных размещений букв бу­дет весьма похож на метод подсчета количества сочетаний. Предположим сначала, что все буквы различны. В таком случае существовало бы 11! способов размеще­ния 11 букв. Теперь обратим внимание, что буква “и" встречается четыре раза. Допуская, что все буквы различны, мы предположили, что каждое размещение букв “и”, которое оставляет все другие буквы на своих местах, отличается от других таких размещений. Теперь все такие размещения нужно считать одинако­выми. Таким образом, 4! размещения четырех букв “и” на самом деле являются одним размещением. Для подсчета количества размещений 11 букв, когда 4 бук­вы “и” уже не рассматриваются как различные, нужно 11! разделить на 4!. Точно так же, для подсчета количества размещений, когда четыре буквы “с” не рассмат­риваются как различные, нужно еще раз разделить на 4!. Осталось рассмотреть две буквы ^ип". Как и предыдущих случаях, каждое размещение букв “п”, которое оставляло все прочие буквы на своих местах и рассматривалось как уникальное, теперь рассматривается как одно и то же размещение. Поскольку существуют 2! способов размещения двух ^мп", то для подсчета количества размещений, когда две буквы “п” не различаются, нужно разделить еще на 2!. Таким образом, получаем

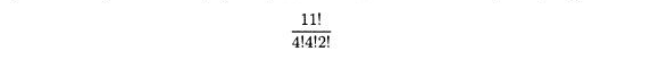различных размещений.

Заметим, что делая буквы неразличимыми, мы игнорируем их порядок, как это было в сочетаниях.

ТЕОРЕМА 8.58. Пусть множество S содержит n объектов k таких различных типов, что имеется n₁ неразличимых объектов типа 1, n₂ неразличимых объектов типа 2, n₃ неразличимых объектов типа 3 и, вообще, n_i неразличимых объекта типа i. Пусть P(n;n₁,n₃,n₃,... ,n_k) — количество различных размещений эле­ментов множества S. Тогда

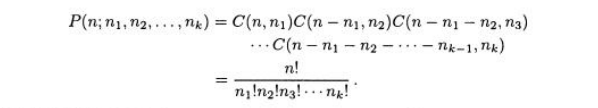ДОКАЗАТЕЛЬСТВО. Рассмотрим первое уравнение. Имеется n мест, которые можно заполнить элементами из S. Существует С(n, n₁) способов выбрать места для n₁ неразличимых объектов типа 1. Если эти места выбраны, то для запол­нения останется n — n₁ мест, поэтому имеются C(n-n₁,n₂) способов выбрать места для n₂ неразличимых объектов типа 2. Если объекты типа 1 и типа 2 вы­браны, то для заполнения остается n — n₁ - n₂ мест, поэтому объекты типа 3

можно разместить С(n – n₁ -n₂,n₃) способами. Аналогично, объекты типа i для 2 ≤ i ≤ k можно выбрать С(n – n₁ – n₂ -… - n_i) способами. Используя

комбинаторный принцип умножения, имеем

способов выбора различных размещений элементов из 5.

Чтобы показать, что

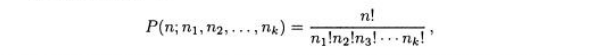воспользуемся рассуждением, которое использовалось неоднократно. Сначала пред положим, что все n объектов из S различны. Если это так, то имеется n! способов разместить данные объекты. Для 1 ≤ r ≤ k, n_i объектов являются неразличи­мыми. Поэтому способы расположения таких объектов, при которых остальные объекты остаются на своих местах, неразличимы. Поскольку имеется n_i! таких расположений, то для нахождения количества различных размещений, когда все n, объектов типа r являются неразличимыми, необходимо n! разделить на n_i! для каждого i. Это дает

что и требовалось доказать.

ПРИМЕР 8.59. Предположим, что 12 книг, включающих 4 одинаковых учебника по математике, 6 одинаковых учебников по информатике, 2 одинаковых учебника по химии, следует расставить на полке. Сколькими способами это можно сделать? Используя предыдущую теорему, имеем

ПРИМЕР 8.60. Сколькими различными способами можно расставить буквы в сло­ве succeeded? Девять букв образуют пять типов неразличимых объектов, вклю­чающих: (1) букву s, (2) букву и, (3) два вхождения буквы с, (4) три вхождения буквы е и (5) два вхождения буквы d. Следовательно, количество неразличимых объектов равно

Заметим, что типы, состоящие только из одного объекта, не влияют на конеч­ный результат. Поэтому следует рассматривать типы, содержащие более одного объекта.

Теперь обобщим биномиальную теорему на случай нахождения коэффици­ентов разложения (х₁ + x₂ + x₃ + … + х_m)ⁿ. Рассмотрим

Для нахождения коэффициента при ab²c необходимо найти все способы выбора а, двух b и с, где буквы выбираются из каждого из сомножителей. Возможные

варианты: abbc, cbba, abcb, dbab, babe, beba, bbac, bbca, cabb, acbb, bacb, bcab. Но это только размещения а, двух b и одного с. Таким образом, количество размещений, которое является коэффициентом при а6²с, равно

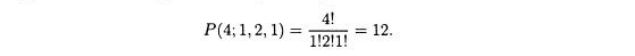Аналогично, коэффициент при b²с² равен

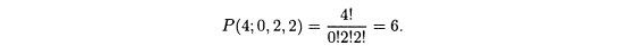ТЕОРЕМА 8.61. Для заданного положительного числа n

где сумма взята по всем неотрицательным целым числам n₁,n₂…n_m таким, что n₁ + n₂ + n₃ +…+ n_m = n.

ДОКАЗАТЕЛЬСТВО. Поскольку (х₁ + х₂ +…+ х_m)ⁿ = (x₁ + х₂ +…+ x_m) (x₁ + х₂ +…+ x_m)…. (x₁ + х₂ +…+ x_m), то каждое слагаемое в разложении получено путем выбора х, из каждого сомножителя в произведении и их перемножения. Для нахождения коэффициента при необходимо найти все воз­можные способы выбора х₁ в количестве n₁, х₂ в количестве n₂, ... и х_m в количестве n_m. Но это есть не что иное, как число размещений х₁ в количестве n₁, х₂ в количестве n₂. ... и х_m в количестве n_m, которое равно

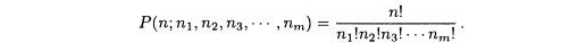ПРИМЕР 8.62. Найдем коэффициент при ab²c³ в разложении (а + b + с)⁶. Этот коэффициент равен

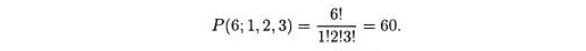ПРИМЕР 8.63. Найдем коэффициент при а³b²с³ в разложении (2а + 3b + c)⁸. Слагаемое имеет вид

поэтому коэффициент равен 4320.

Предположим, что имеются семь различимых шаров, и требуется положить три шара в первую коробку, два шара — во вторую и два шара — в третью коробку. Сколькими способами можно это сделать? Существует С(7,3) способов выбрать три шара для первой коробки. После того, как шары выбраны, остается четыре шара, два из них выбираются для второй коробки. Для этого существуют С(4,2) способов. Наконец, остается два шара, которые мы кладем в последнюю коробку.

Это может быть сделано С(2,2) или одним способом. Таким образом, количество способов размещений шаров равно С(7,3) • С(4,2) • С(2,2). Но по теореме 8.58 это равно

Как видим, существует связь между размещениями неразличимых объектов и разбиением множества, что, по сути, мы и делали с шарами и коробками. Для того, чтобы выявить эту связь, рассмотрим следующий пример. Предположим, что имеются два красных, три зеленых и четыре синих шара, которые отличают­ся только цветом. Требуется найти все возможные различные размещения данных шаров. Пусть s₁,s₂,s₃,s₄,s₅,s₆,s₇,s₈,s₉ ^— позиции, в которые шары могут быть помещены. Допустим, красные шары располагаются в позициях s₂ и s₇. Отожде­ствим такое размещение с помещением s₂ и s₇ в коробку R. Предположим, что зеленые шары находятся в позициях s₁, s₃ и s₉. Отождествим это с помещением s₁, s₃ и s₈ в коробку G. Предположим, наконец, что синие шары располагаются в позициях s₄,s₄, s₆ и s₈. Отождествим это с помещением s₃ s₄, .s₅, и s₆ в короб­ку В. Обратно, если s₁ и s₉ помещены в коробку R, s₂ s₇ и s₈ — в коробку G, а s₃, s₄, s₅ и s₆ — в коробку В, мы отождествим это с помещением красных шаров в позиции s₁ и s₉, зеленых шаров — в позиции s₂, s₇ и s₈. а синих шаров — в позиции s₃, s₄, s₅ и s₆ - Таким образом, задача о размещении неразличимых ша­ров свелась к задаче о помещении шаров в коробки. В общем случае справедлива следующая теорема.

ТЕОРЕМА 8.64. Пусть C(n; n₁, n₂,n₃... ,n_m) — количество разбиений множества S, содержащего n элементов на m множеств S₁ S₂, S₃, ... и S_m, содержа­щих n₁, n₂, n₃ ... и n_m элементов соответственно. Тогда

ДОКАЗАТЕЛЬСТВО. Существуют C(n,n₁) способов выбора элементов для S₁. Как только эти элементы выбраны, остается n – n₁ элементов, из которых необ­ходимо выбрать n₂ элементов для S₂. Последнее можно осуществить C(n - n₁,n₂) способами. Если эти элементы выбраны, остаются n – n₁ - n₂ элементов, из ко­торых необходимо выбрать n₃ элементов для S₃. Предположим, что множества S₁, S₂, S₃. ... и S_i-1 уже выбраны, тогда для выбора n, элементов для множества S_i остается n – n₁ — n₂ — … n_i-1 элементов. Этот выбор можно осуществить С(n - n₁ - n₂ - … - n_i-1 ,n_i) способами. Используя принцип умножения, получаем

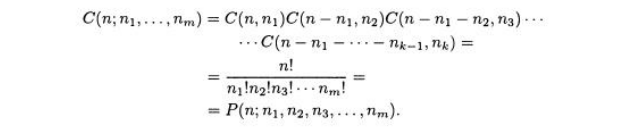Заметим, что сочетание С(n,k) = С(n;k,n - k) является частным случаем разби­ения n-элементного множества на множество, содержащее k элементов (которые

мы выбираем), и множество, содержащее n — k элементов (которые остаются). Важно отметить, что множество разбивается в последовательность подмножеств с заданным количеством элементов. При этом мы подсчитывем количество разби­ений множества в последовательность подмножеств заданных размеров. Один из способов убедиться в этом — заметить, что С(n,k) = С(n;k,n - k) — количество способов выбрать k объектов из n объектов. Мы не включаем сюда количество способов выбрать n - k объектов и, следовательно, оставляем к объектов, что также дает разбиение множества S, содержащего n объектов, на подмножества, содержащие k и n - k объектов. Для этого также существуют С(n;k, n - k) спо­собов, поэтому существуют 2С(n;k,n - k) способов разбиения множества S на множества, содержащие k объектов и n - k объектов. Другой способ представить себе содержание теоремы — это рассматривать ее как описание раскладывания различимых шаров в разные коробки.

ПРИМЕР 8.65. Сколькими способами можно выбрать четыре набора по пять карт из колоды, содержащей 52 карты? По сути, колода разбивается на пять множеств: четыре набора по пять карт и 32 оставшихся карты. Поэтому количество таких наборов равно