8.8. Принцип клеток

Принцип клеток, известный также как принцип Дирихле, — это очень простая, но тем не менее очень мощная идея. Она особенно полезна в теории чисел. Данный раздел состоит из двух довольно простых теорем и нескольких не совсем простых примеров. Начнем с наиболее известной формы принципа клеток.

ТЕОРЕМА 8.75. Если поместить n + 1 голубей в n клеток, то, по крайней мере, в одной клетке будет находится более одного голубя.

ДОКАЗАТЕЛЬСТВО. Если в каждой клетке не более одного голубя, то голубей не может быть больше, чем клеток. Тогда во всех клетках должно быть не более, чем n голубей, что противоречит условию.

Из теоремы следует, что если m > n и требуется m голубей разместить в n клетках, то в одной клетке находится более одного голубя.

ПРИМЕР 8.76. В списке, содержащем m + 1 положительных целых чисел, по крайней мере, два числа имеют один и тот же остаток при делении на m. Пусть

a₁,a₂,a₃ … ,a_m,a_m+i — перечень положительных целых чисел. Предположим, что для 1 ≤ i ≤ m + 1 имеем a_i = q_im + r_i, где 0 ≤ r_i ≤ m. Следовательно, r₁,r₂,r₃ … ,r_m,r_m+i — список, содержащий m + 1 положительных целых чисел, меньших m. Но существует только m различных неотрицательных чисел, мень­ших m. Поэтому два числа из r_i должны быть равны.

ПРИМЕР 8.77. Если |А| > |В|, то не может существовать инъективная функция f : А → В. Пусть |В| = n. Существует п множеств f^~l(b) = {х : f(x) = b) для содержит больше n элементов. Поэтому не менее двух элементов, например, а и а', должны быть в одном множестве. Но тогда f(а) = f(а') и f не является инъективной функцией.□

ПРИМЕР 8.78. Если в прямоугольнике со сторонами 6 и 8 дюймов помещены пять точек, то существуют две точки, расстояние между которыми не более 5 дюймов. Разделим исходный прямоугольник на четыре прямоугольника, размером 3 на 4 дюйма каждый. Поскольку пять точек должны находиться либо внутри, либо на границах четырех прямоугольников, то хотя бы две точки должны быть либо внутри, либо на границе одного и того же прямоугольника размера 3x4. Но любые такие точки находятся на расстоянии не более 5 дюймов. □

ПРИМЕР 8.79. В последовательности a₁,a₂,a₃ … ,a₁₀ из десяти целых чисел су­ществует последовательность идущих подряд элементов a_m,a_m+1,a_m+2 … ,a_m+n, сумма которых делится на 10. Рассмотрим числа s₁ = а₁ s₂ = a₁ + a₂. s₃ = a₁ + a₂ + а₃, … , s₁₀ = a₁ + а₂ + а₃ + a₄ + … + a₁₀. Если одна из этих сумм делится на 10, то процесс завершен, элементы суммы образуют искомую последовательность. Если нет. то каждое s_i = 10q_i + r_i, где 1 ≤ r_i ≤ 9. Имеется десять r_i , и только девять значений, которые они могут принимать. Поэтому существуют два r с одинаковыми значениями, например, r_j = r_i для некоторого j < k. Тогда

кратно 10. Но это не что иное, как сумма a_j+1 + а_j+2 + а_j+3 + a_j+4 + … + a_k, элементы которой образуют искомую последовательность.

ПРИМЕР 8.80. (Эрдош и Шекерес) Пусть S — подмножество множества {1,2,3,... ,2n}, содержащее n+1 элемент, где n — некоторое положительное целое число. Существуют два элемента, принадлежащие множеству S такие, что один элемент делит другой элемент. Любое положительное целое число можно представить в виде 2ⁱq_i, где q_i — положительное нечетное число. Запишем каждый элемент множества S в таком виде. Множество {q₁,q₂, … , q_n,q_n+1»} содержит n + 1 по­ложительных нечетных целых чисел, при том что имеется только n нечетных чисел, которые меньше или равны 2n. Поэтому q_i = q_j при i ≠ j. Таким образом, множество S содержит два различных целых числа вида а = 2^rq_i и b = 2⁸q_i соответственно. Если r < s, то а делит b, и если r > s, то b делит а.

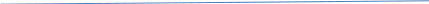
А теперь приведем более сильные формы принципа клеток.

ТЕОРЕМА 8.81.

а) Пусть m > n голубей помещены в n клеток, тогда некоторая клетка содержит не менее голубей.

б) Пусть m = m₁ + m₂ + m₃ + … + m_n - n + 1 голубей помещены в n клеток, где m_i — положительное целое число для каждого 1 ≤ i ≤ n. Тогда, для некоторого i, i-ая клетка содержит не менее m_i, голубей.

ДОКАЗАТЕЛЬСТВО, а) Пусть каждая клетка содержит меньше [ ] голубей. Тогда, поскольку нас интересуют целые голуби, каждая клетка содержит меньше голубей. Поэтому общее количество голубей меньше их n x = m, что противо­речит условию.

б) Пусть i-ая клетка содержит меньше, чем m, голубей. Тогда количество голубей в i-ой клетке меньше или равно m_i - 1. Просуммировав по всем клеткам, получаем, что всего голубей не более, чем

что противоречит условию.

ПРИМЕР 8.82. Пусть в урне находятся 10 красных. 10 синих и 10 зеленых ша­ров. Сколько шаров нужно взять из урны, чтобы с уверенностью иметь хотя бы 4 красных или 5 синих, или 6 зеленых шаров? Мы знаем, что 12 шаров недоста­точно, поскольку можно выбрать 3 красных, 4 синих и 5 зеленых шаров. Если отождествить шары одного цвета с голубями, находящимися в одной клетке, то, согласно части (б) сильной формы принципа клеток, имеем n = 3, m₁ = 4, m₂ = 5 и m₃ = 5. Поэтому искомое количество шаров равно

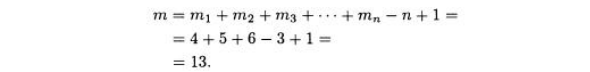ПРИМЕР 8.83. (Эрдош и Шекерес) Конечная последовательность целых чисел a₁, а₂, а₃ … а_к возрастающая, если каждое число последовательности больше предыдущего. Иначе говоря, если i > j, то а_i > а_j. Конечная последовательность целых чисел a₁, а₂, а₃ … а_к убывающая, если каждое число последователь­ности меньше предыдущего. Иначе говоря, если i > j, то a_i < a_j. Любая по­следовательность из n² + 1 различных целых чисел содержит либо убывающую подпоследовательность, включающую не менее n + 1 членов, либо возрастающую подпоследовательность, включающую не менее n + 1 членов. Для доказательства предположим, что s_i — количество чисел в самой длинной возрастающей последовательности a₁, а₂, а₃ … а_n2+1, начинающейся с а_i. Если > n + 1 для некоторого i, то процесс завершен. Если нет, то для каждого r, 1 ≤ s_i ≤ n. По­этому для всех n² + 1 штук s_i. где 1 ≤ i ≤ n² + 1, имеется n значений. Согласно части (а) сильной формы принципа клеток получаем, что

штук s_i равны. Поэтому, по крайней мере, n + 1 чисел из s_i равны. Пусть все они равны s. Рассмотрим подпоследовательность длины n + 1, состоящую из таких что s, равны s. Эта последовательность — убывающая, потому что если a_i > a_j для i > j, то, добавляя a_i в начало последовательности длины s, начинающейся с a_j можно получить возрастающую последовательность длины s+ 1, начинающуюся с а_i. Но это противоречит тому факту, что самая длинная возрастающая последовательность, начинающаяся с а_i, имеет длину s. Таким образом построена убывающая последовательность длины n + 1.

ПРИМЕР 8.84. Предположим, что в комнате находятся шесть человек, и каждые два из них либо друзья, либо враги. Тогда есть три человека, которые дружат между собой, или есть три человека, которые враждуют между собой. Выберем одного человека, назовем его А и поставим в середине комнаты. Разместим всех его врагов вдоль южной стены, а всех друзей — вдоль северной стены. Согласно части (а) сильной формы принципа клеток либо не менее трех человек стоят вдоль южной стены, либо не менее трех человек стоят у северной стены. Если у южной стены стоит не менее трех человек, то или трое из них — взаимные друзья, что и требовалось доказать, или двое из них — враги. Тогда эти люди вместе с А — трое взаимных врагов. Аналогично, если не менее трех человек стоят у северной стены, то или трое из них — взаимные враги, что и требовалось доказать, или двое из них — друзья. Тогда они вместе с А — трое взаимных друзей.

Рассмотренный выше пример является характерным, хотя и довольно про­стым примером задач из раздела комбинаторики, который носит название теория Рамсея Можно считать, что нам повезло, поскольку в теории Рамсея очень мало простых примеров. Почти все ее проблемы по сей день не решены. Поясним тео­рию Рамсея на примере полного графа с раскрашенными ребрами. Предположим, что в предыдущем примере вершины графа — аналоги людей. Образуем граф сле­дующим образом: если двое людей — друзья, то соответствующие им вершины соединяет красное ребро. Если двое людей — враги, то соответствующие вершины соединяет синее ребро. Поскольку каждые двое — либо друзья, либо враги, то ребро существует между двумя любыми вершинами графа. Следовательно, этот граф — граф К₆, полный граф с шестью вершинами.

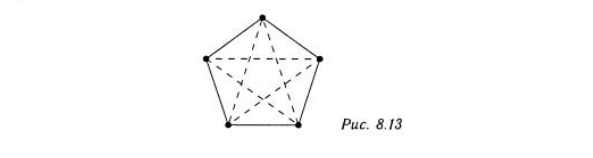
В рассмотренном выше примере, утверждалось, что если все ребра графа K₆ раскрашены либо красным, либо синим цветом, то в графе К₆ имеется ли­бо красный треугольник, либо синий треугольник, каждый из которых является подграфом графа К₆, по сути, просто графом К₃. Граф К₅ не обладает таким свойством, что если его ребра раскрашены либо красным, либо синим цветом, то он содержит красный или синий подграф К₃. Это доказывает граф, изображенный на рис. 8.13, где пунктиром изображены красные ребра, а синей линией — синие ребра.

Теперь дадим определение свойства Рамсея для двух цветов на примере графов. Существует обобщение свойства Рамсея для произвольного числа цветов.

ОПРЕДЕЛЕНИЕ 8.85. Полный граф К_п обладает (р, q) свойством Рамсея,

если в случае, когда он раскрашен двумя цветами, например, красным и синим, он содержит либо подграф К_р с красными ребрами, либо подграф К_q с синими ребрами.

ОПРЕДЕЛЕНИЕ 8.86. Число Рамсея, R(р, q) — это наименьшее число n такое, что граф К_n имеет (p,q) свойство Рамсея.

Вполне очевидно, что R(p,q) = R(q,p), поскольку можно заменить красный цвет на синий, а синий — на красный. Также, если m > R(p,q) = n, то, поскольку К_n — подграф графа К_m, граф К_m также обладает свойством Рамсея.

Относительно чисел Рамсея будут доказаны только две теоремы. Эти теоре­мы интересны сами по себе, но более важным является то, что они доказывают существование чисел Рамсея.

ТЕОРЕМА 8.87. Для всех р ≥ 2 R(p, 2) = R(2,p) = p.

ДОКАЗАТЕЛЬСТВО. Рассмотрим граф К_р. Если одно ребро раскрашено красным (или синим) цветом, то существует красный (или синий) граф К₂. Если нет, тогда все ребра раскрашены синим (красным ) цветом, и мы получаем синий (красный) граф К_р.

ТЕОРЕМА 8.88. (Эрдош и Шекерес) Для всех p,q ≥ 3

ДОКАЗАТЕЛЬСТВО. Предположим, что К — полный граф. имеющий R(p-l,q) + R(p, q - 1) вершин, ребра которого раскрашены в красный или синий цвет. Пусть u — выбранная вершина графа К. Пусть N — полный подграф графа К, вершины которого V_N связаны с вершиной u красным ребром. Пусть S — полный подграф графа K, вершины которого Vs связаны с вершиной u синим ребром. Поскольку V_N U V_s содержит

вершин, разделенных на n = 2 множества, то либо V_N имеет R(p - 1 ,q) вершин, либо V_S имеет R(p.q — 1) вершин. Поэтому, либо N — полный граф, имеющий R(р—1,д) вершин, либо S — полный граф, имеющий R(p,q-l) вершин. Если N — полный граф, имеющий R(p — 1 ,q) вершин, то он содержит либо подграф К_р-1 со всеми красными ребрами, либо подграф К_q со всеми синими ребрами. Если он содержит граф К_p-1 со всеми синими ребрами, то доказательство завершено. Если он содержит граф К_р-1 со всеми красными ребрами, то, добавив вершину u и все красные ребра из u в вершины подграфа К_р-1, получим полный граф К_р со всеми красными ребрами, что и требовалось доказать.

Аналогично, если S — полный граф, имеющий R(p,q - 1) вершин, то он содержит либо подграф К_р со всеми красными ребрами, либо подграф K_q-1 со всеми синими ребрами. Если он содержит граф К_р со всеми красными ребрами, то доказательство завершено. Если он содержит граф К_q­-1 со всеми синими вершинами, то если добавить вершину и и все синие ребра из вершины u во все вершины подграфа K_q-1, получим полный граф K_q, с синими ребрами, что и требовалось доказать.

Основываясь на результатах двух приведенных выше теорем и используя индукцию или принцип полного упорядочения для положительных целых чисел, а также технику доказательства второй теоремы, можно доказать еше один ре­зультат, сформулированный в виде следующей теоремы

ТЕОРЕМА 8.89. (Рамсей) . Если целые числа р и q больше единицы, то число Рамсея. R(p, q), существует.