Элементы квантовой статистики

Фазовое пространство. Функция распределения. Рассмотрим систему из N частиц. Свяжем с ней многомерное пространство всех координат и импульсов частиц системы. Состояние системы определяется заданием переменных 6N, так как состояние каждой частицы определяется тройкой координат x, y, z и тройкой проекций импульса , , . Поэтому размерность многомерного пространства равно 6N. Это пространство называется фазовым пространством. Каждому микросостоянию системы в классическом случае отвечает точка в фазовом пространстве. При квазиклассическом описании движения системы на каждое квантовое состояние системы приходится в этом пространстве элементарный объем .

При взаимодействии с окружающей средой состояние системы меняется. Вероятность dP некоторого состояния системы (p, q) можно представить с помощью функции распределения

(8) Здесь означает произведение дифференциалов координат и импульсов всех частиц. По определению функции распределения

, где интегрирование производится по всему фазовому пространству.

При известной функции распределения можно определить макроскопические параметры системы. Любой макроскопический параметр L в смысле статистической физики является средним по микросостояниям

. (9)

Явное выражение функции распределения для системы, находящейся в тепловом контакте с большим тепловым резервуаром было получено Гиббсом. Оно называется каноническим распределением Гиббса и имеет вид

, где A – нормировочная постоянная, n – совокупность квантовых чисел, определяющих данное состояние.

Статистика Бозе-Эйнштейна и Ферми-Дирака. Наиболее простым объектом для изучения является идеальный газ. Реальный газ можно считать идеальным, если взаимодействие частиц несущественно. Состояние системы невзаимодействующих тождественных частиц можно характеризовать с помощью чисел заполнения , определяющих среднее число частиц в i-м квантовом состоянии.

Для систем частиц, образованных бозонами, числа заполнения могут принимать любые целые неотрицательные значения: 0, 1, 2, …. Для систем, образованных фермионами, числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых. Сумма всех чисел заполнения равна числу частиц системы. С помощью канонического (или большого канонического) распределения Гиббса можно определить числа заполнения квантовых состояний.

Числа заполнения идеального газа бозонов – бозе-газа – определяются соотношением

. (10) Это выражение называется распределением Бозе-Эйнштейна. Здесь – среднее число бозонов в квантовом состоянии с энергией ,  – параметр, который называется химическим потенциалом. Его величина определяется из условия , где N – число частиц в системе. Химический потенциал по своему определению является функцией числа частиц и температуры .

Распределение фермионов по энергиям имеет вид

. (11) Смысл входящих в (11) величин тот же, что и в (10). Распределение (11) называется распределением Ферми-Дирака.

Если , то распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла-Больцмана

, (12) где . Таким образом, при малых числах заполнения ( ) оба квантовых газа ведут себя подобно классическому газу.

Квантовый газ называется вырожденным, если числа заполнения сравнимы с единицей или больше ее (последнее возможно для бозе-газа). Вырожденный бозе-газ и ферми-газ существенно отличаются друг от друга и в свою очередь от идеального газа. Так в вырожденном бозе-газе при понижении температуры происходит бозе-конденса­ция, когда на нижний энергетический уровень переходит большое число частиц. Бозе-конденсацией объясняются такие явления как сверхтекучесть и сверхпроводимость.

Вырождение газов наступает при понижении температуры и/или повышении плотности газа. В качестве параметра вырождения квантового газа используется температура , при которой . Эта характеристическая температура называется температурой вырождения.

Фотонный газ. Согласно квантовым представлениям тепловое излучение можно рассматривать как равновесный газ фотонов. Спин фотона равен единице, и поэтому, фотоны являются бозе-газом и подчиняются статистике Бозе-Эйнштейна. Так как фотоны непрерывно излучаются и вновь поглощаются стенками полости, то полное число фотонов не фиксировано. Это означает, что химический потенциал фотонов равен нулю и распределение фотонов по энергиям имеет вид

. Для определения внутренней энергии и полного числа фотонов требуется определить плотность состояний. Воспользуемся общим правилом, согласно которому число одночастичных квантовых состояний – орбиталей, приходящихся на шестимерный фазовый объем , равно

. Для фотонов и . Число орбиталей, приходящихся на частотный интервал d, очевидно равно , где – спектральная плотность орбиталей. Множитель 2 учитывает две поляризации фотона. Для спектральной плотности энергии излучения найдем

. (1) Соотношение (1) есть формула Планка. Таким образом, статистика Бозе-Эйнштейна для фотонного газа приводит к законам теплового излучения (формуле Планка и др.).

Фононы. Теплоемкость кристалла. Тепловое движение кристаллов во многих отношениях напоминает равновесное электромагнитное излучение. Это связано с тем, что движение атомов при малых отклонениях от положения равновесия может рассматриваться как набор гармонических колебаний. Так как колебания атомов являются, благодаря сильному взаимодействию, связанными, то тепловое движение решетки кристалла представляет собой суперпозицию упругих монохроматических волн с разными частотами и направлениями распространения.

Как и для электромагнитной волны, импульс и энергия упругой волны связаны соотношением , где c – скорость звука. Однако между ними есть и различия. Электромагнитные волны поперечны и обладают двумя независимыми поляризациями. Волны в кристалле могут быть как поперечными, с двумя независимыми поляризациями, так и продольными. Кроме того, набор электромагнитных волн не ограничен по частотам и существуют волны со сколь угодно большими частотами. Для волн в кристалле из-за дискретности решетки длина волны не может быть меньше минимального расстояния между атомами. Следовательно, частоты колебаний решетки ограничены сверху и общее число различных волн в кристалле конечно.

Полное число различных колебаний равно , так как из полного числа степеней свободы 3N надо вычесть три поступательные и три вращательные степени свободы твердого тела как целого; здесь N – атомов в кристалле. Классическая теория для внутренней энергии и теплоемкости твердого тела дает простые предсказания. Согласно закону равнораспределения каждая степень свободы колебательного движения вносит вклад, равный kT. Тогда для одного моля

и, следовательно,

. (2) Это утверждение называется законом Дюлонга и Пти и для ряда веществ хорошо выполняется при комнатных температурах. Однако для некоторых кристаллов (например, для алмаза), закон Дюлонга и Пти нарушается уже при комнатных температурах, а при низких температурах теплоемкость любых кристаллов становится существенно меньшей, чем 3R.

Для описания тепловых колебаний в решетке используется идея особых квантовых частиц – фононов. Так же как для фотонов, число фононов на орбитали не ограничивается. Следовательно, фононы подчиняются распределению Бозе-Эйнштей­на. Фононы непрерывно излучаются и поглощаются кристаллической решеткой, и поэтому химический потенциал фононного газа следует положить равным нулю.

Запишем распределение Бозе-Эйнштейна и выражение для внутренней энергии идеального фононного газа

, , (3) где и суммирование ведется по всем фононным состояниям. Для вычисления энергии надо знать спектр частот кристаллической решетки . Его нахождение представляет нетривиальную задачу даже для сравнительно простых решеток.

Используем для расчета внутренней энергии и теплоемкости кристалла так называемую непрерывную модель. Кроме этого, предположим, что скорости всех упругих волн одинаковы. Такое предположение не вполне корректно, но оно позволяет упростить вычисления и получить основные результаты. В результате оказывается, что спектральная плотность фононных орбиталей отличается от фотонной плотнос­ти множителем (у фотона две поляризации, у фонона – три). Поэтому, для фононов

. и формула (3) переходит в интеграл

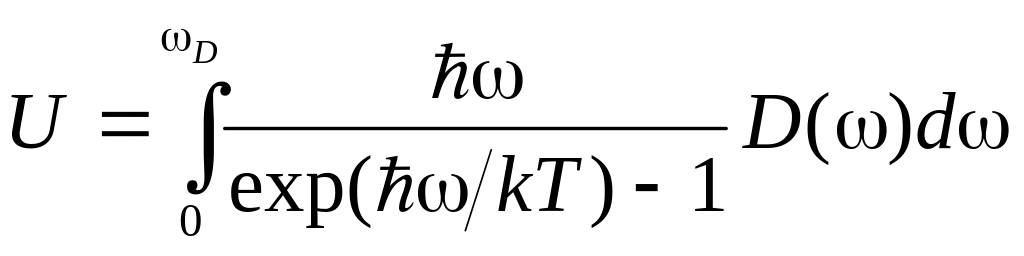. (4) Верхний предел интегрирования в (4) равен дебаевской частоте , а не бесконечен, как в случае фотонов. В теории Дебая она определяется соотношением

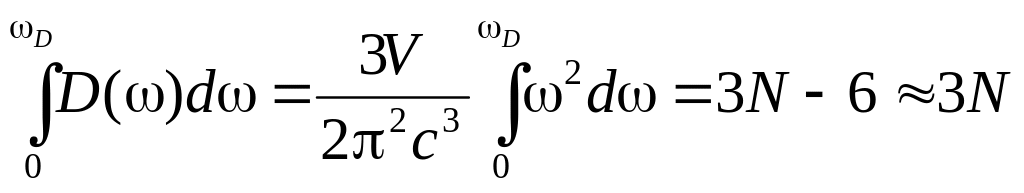. В итоге получаем

.

Введем в (4) новую переменную интегрирования и определим характеристическую температуру Дебая формулой . Тогда выражение для внутренней энергии примет вид

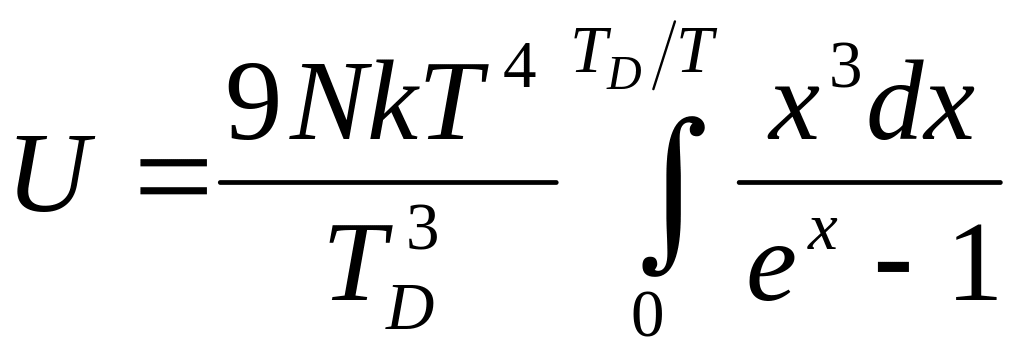. (5)

При высоких температурах формула (5) приводится к виду

. В этом случае в согласии с законом Дюлонга и Пти.

При низких температурах верхний предел интегрирования в (5) можно положить равным бесконечности (соответствующее значение интеграла равно ). В результате получаем для энергии

, для теплоемкости

. (6) Этот результат известен как закон Дебая.

Вырожденный электронный газ в металле. Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми-Дирака. Рассмотрим вначале электронный ферми-газ при температуре абсолютного нуля – полностью вырожденный ферми-газ. При распределение электронов по состояниям ведет себя как ступенчатая функция

(7) В формуле (7) величина – предельное значение химического потенциала при , а – ступенчатая функция. Физический смысл (7) очевиден. При фермионы заполняют самые низкие энергетические уровни. По принципу Паули каждое состояние может быть занято только одним электроном. Поэтому уровни до при являются занятыми, причем для этих уровней , а вышележащие уровни свободны . Максимальная энергия электронов , равная предельному значению химического потенциала, называется энергией Ферми.

В импульсном пространстве электроны также заполняют все состояния с импульсами от нуля до максимального импульса . Число квантовых состояний в интервале импульсов от p до pdp равно , где множитель 2 учитывает кратность спинового вырождения. Число электронов с импульсами от нуля до максимального импульса равно

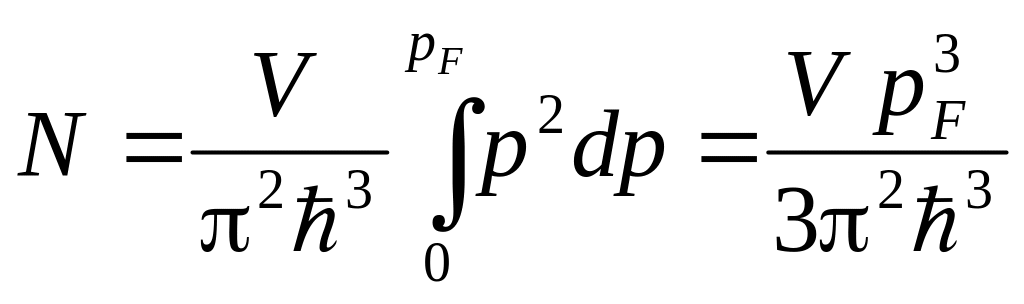. Отсюда для граничного импульса – импульса Ферми – имеем

( – концентрация электронов проводимости), а для энергии Ферми находим

. Наконец, полная энергия газа равна

. Согласно уравнению состояния идеального газа находим давление ферми-газа при

. Таким образом, даже при температуре абсолютного нуля давление электронного газа отлично от нуля. Для см^–3 имеем атм. Это обстояте­льство является следствием того, что электроны не находятся в покое даже при .

При температурах, отличных от нуля, часть электронов переходит с уровней, лежащих ниже уровня Ферми , на уровни, лежащие выше этой границы. В результате ступенька расплывается и превращается в пунктирную линию (рис.). Из формулы распределения Ферми-Дирака легко видеть, что полуширина распределения . Поэтому температуру естественно назвать температурой вырождения электронного газа (ступенька полностью расплывается). При более высоких температурах вырождение снимается, – электронный газ ведет себя как классический. Численная оценка приводит к значению К. Следовательно, электронный газ в металлах при любых температурах вплоть до точки плавления остается вырожденным.

Вычисления внутренней энергии для температур меньших температуры вырождения приводят к формуле

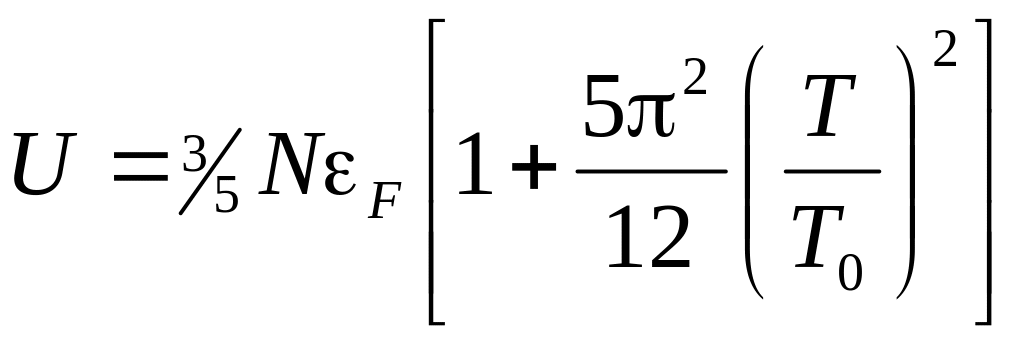. Отсюда теплоемкость электронного газа

. (8)

Если рассматривать электроны проводимости в металле как классический электронный газ, то согласно закону равномерного распределения энергии по степеням свободы эти электроны должны были бы дать добавочный вклад в теплоемкость, равный . Согласно (8) вклад электронов в теплоемкость металла оказывается меньше этого значения на два порядка, в соответствии с опытом.