§3. Формула остроградского – гаусса.

Пусть - область. В G задано векторное поле .

В декартовой системе координат .

Df.1 , т.е. существуют все частные производные и они непрерывны в G.

Df.2 Дивергенцией (расходимостью) векторного поля в точке M(x,y,z) называется скаляр:

(1)

Отметим, что операция ставит в соответствие векторному полю скалярное поле , определенное в G.

Дивергенция в заданной точке характеризует мощность источников и стоков в данной точке.

Те точки, где > 0 называются источниками поля, а те где < 0 – стоками.

Абсолютная величина дивергенции характеризует производительность (интенсивность) источников и стоков. Если , то в точке М нет ни источника, ни стока.

Th.1 (ОСТРОГРАДСКОГО - ГАУССА)

Пусть область можно представить в виде объединения конечного числа областей , каждая из которых является одновременно:

-цилиндром, - цилиндром и -цилиндром, тогда - кусочно-замкнутая гладкая поверхность. ограничивающая G. Поле .

Тогда справедлива формула Остроградского – Гаусса:

(2)

* Причем, поверхностный интеграл берется по внешней стороне поверхности.

Доказательство:

Скалярный вид формулы Остроградского – Гаусса:

(3)

Пусть в G z- цилиндроид, т.е.:

.

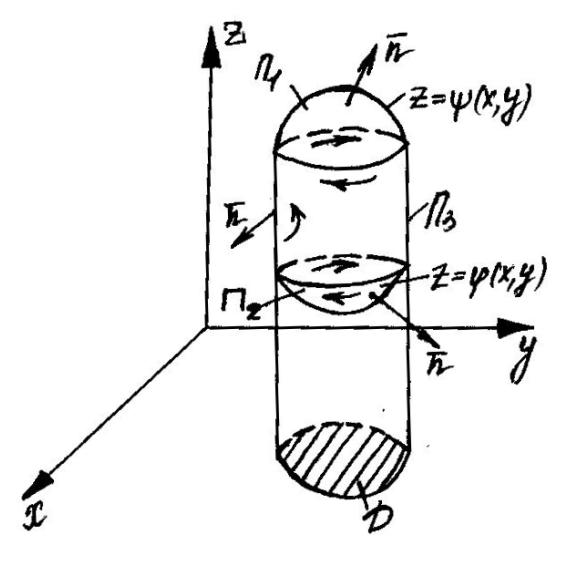
Тогда: -гладкие.

Докажем формулу:

(4)

= (по теореме 5 и формуле (9))= .

Пусть теперь G является также и - цилиндроидом и -цилиндроидом. Тогда аналогично можно показать, что:

(5)

(6)

Суммируя (4), (5) и (6) получим (3).

Пусть теперь G – объединение областей указанного типа: .

П

- гладкая. тогда:

(*)

(**)

- две стороны одной поверхности (с нормалями ). Отсюда скалывая, получим:

формула (2).

Заметим, что теорема Остроградского – Гаусса справедлива для областей более общего вида.

СЛЕДСТВИЕ.

- область, инвариантен относительно системы координат, т.е. не зависит от выбора системы координат.

Доказательство:

. Пусть - открытая область, для которой верна теорема Остроградского – Гаусса. , - замкнутая поверхность. ограничивающая H. Тогда:

По теореме о среднем для кратных интегралов:

.

Отметим, что , т.к. .

(***)

Перейдем в (***) к при . В силу непрерывности , получим:

(7)

Т.к. поток и не зависят от системы координат не зависит от выбора системы координат. Из (7) физический смысл . Пусть - скорость жидкости. - средняя объемная плотность потока жидкости через поверхность , ограничивающая область H с объемом V.

- плотность источника в точке .

Из (7) , что при > 0 – сток, =0 – источник отсутствует.

Таким образом в какой-нибудь точке равен потоку векторного поля через бесконечно малую замкнутую поверхность, окружающую данную точку, отнесенному к единице объема.

Df.2 Пусть определено в G, называется соленоидальным в G, если .

Th.2 (НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ

СОЛЕНОИДАЛЬНОСТИ ПОЛЯ )

Пусть G – область, для которой возможно применение формулы Остроградского – Гаусса. - замкнутая кусочно-гладкая, , тогда соленоидально в G.

Доказательство:

Необходимость:

Пусть соленоидально в G . Пусть - область допускающая применение формулы Остроградского – Гаусса. Тогда по (7):

в G.

Достаточность:

Пусть . Пусть - допускает применение формулы Остроградского – Гаусса, по ней:

соленоидальное.