Глава 12. Элементы теории поверхностей.
Раннее мы встречались с поверхностями, задаваемыми либо в явном виде z=f(x,y), либо в неявном виде F(x,y,z)=0.
Рассмотрим более общий случай задания поверхности.
Df.1
Пусть
- область,
- замыкание области.
Поверхностью П
в пространстве
непрерывное
отображение области
в пространство
:
V z
П
U y
x
Df.2
Пусть П
задана
…..(1),
.
Тогда
поверхность
класса
,
если
имеет в области
непрерывные производные до «n
– го» порядка включительно, т.е.:
или
;
.
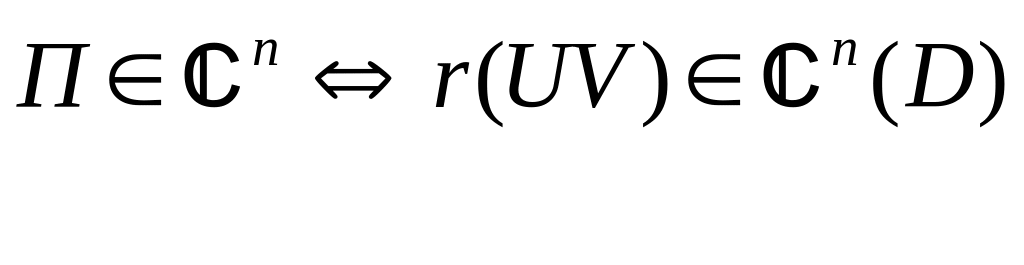Уравнение (1) эквивалентно трем уравнениям:
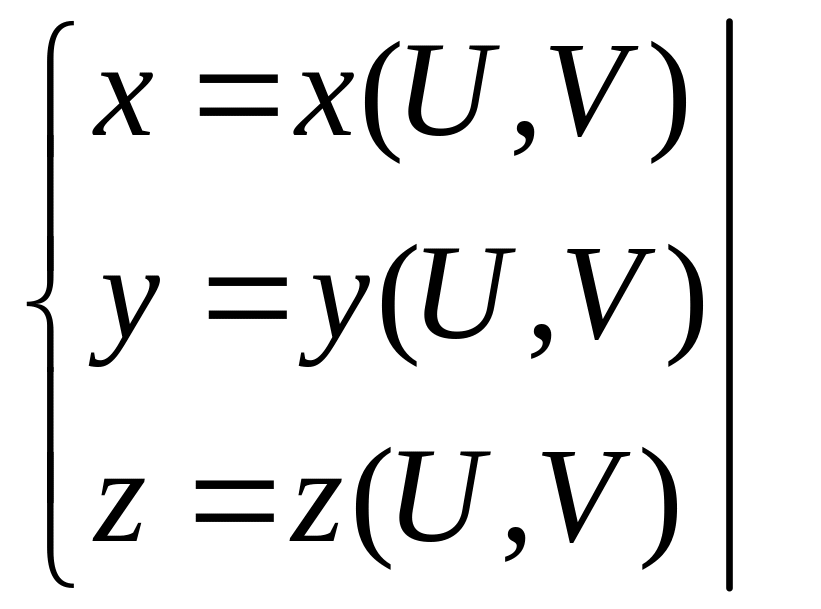(2)
.
Уравнения (1)
и (2)
называются параметризацией поверхности
П.
Напомним, что под производными
понимаются вектора:
(3)
Более сокращенно
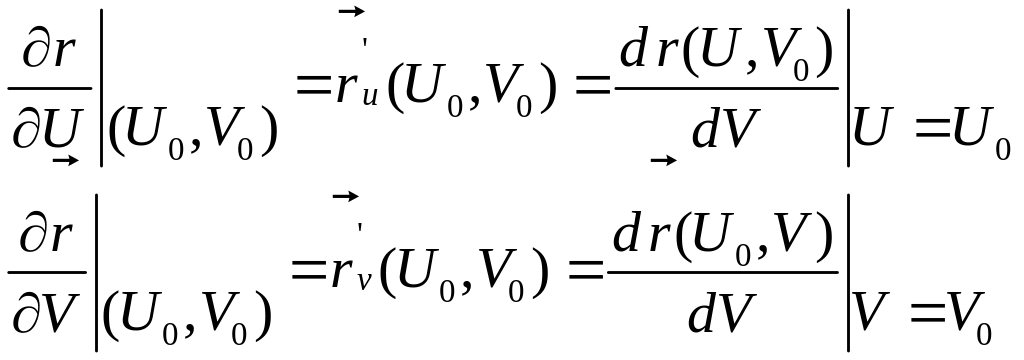
Также определяются
производные высших порядков
,
где
.
Пусть
.
Составим матрицу Якоби.
(4)
Матрица Якоби
отображение
.
Df.3
П
называется гладкой, если
и
.
Т.к.
линейная
независимость строк
не коллинеарны, т.е.
.
Но
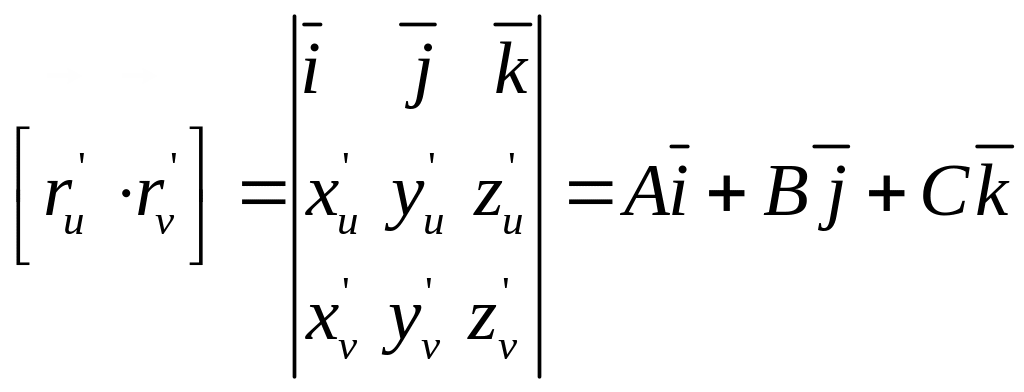(5)
А, В, С – миноры матриц второго порядка.
Тогда
.
Рассмотрим точку
,
причем
.
Если зафиксировать
,
то получим параметрическое уравнение
линии:
(6)
При фиксированном
,
получаем линию:
(7)
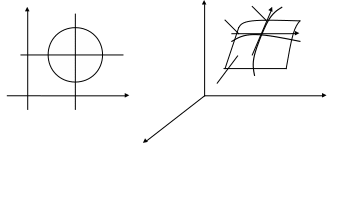
Линии (6) и (7) образуют два семейства линий на поверхности П.
(Сравним с отображением плоских областей).
V
z
Как известно
касательные вектора к этим линиям в
точке
получены следующим образом: к линии
К
линии
Для касательной
плоскости – эти вектора направляющие
нормальный
вектор:
(8)
НАПРИМЕР.
,
(9)
П
0
D
x
Кроме гладких поверхностей будем рассматривать кусочно-гладкие.
Df.4 П – называется кусочно-гладкой поверхностью, если можно разбить на конечное число гладких поверхностей. Причем эти части имеют общими только куски границы.
