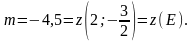- •Функції багатьох змінних
- •Тема 10.1. Функції двох змінних.
- •Тема 10.2. Похідні і диференціали функцій декількох змінних.
- •Тема 10.3. Дотична площина і нормаль до поверхні.
- •Тема 10.4. Екстремум функції двох змінних.
- •10.4.1. Основні поняття.
- •10.1. Функції двох змінних
- •10.1.1. Основні поняття
- •10.1.2. Границя функції
- •10.1.3. Неперервність функції двох змінних
- •10.1.4. Властивості функцій, неперервних в обмеженій замкненій області
- •10.2. Похідні і диференціали функцій декількох змінних
- •10.2.1. Частинні похідні першого порядку та їх геометричний зміст
- •Геометричний зміст частинних похідних функції двох змінних
- •10.2.2. Частинні похідні вищих порядків
- •10.2.3. Диференційовність і повний диференціал функції.
- •10.2.4. Застосування повного диференціала для наближених обчислень
- •10.2.5. Диференціали вищих порядків
- •10.2.6. Похідна складної функції. Повна похідна
- •10.2.7. Інваріантність форми повного диференціала
- •10.2.8. Диференціювання неявної функції
- •10.3. Дотична площина і нормаль до поверхні
- •10.4. Екстремум функції двох змінних
- •10.4.1. Основні поняття
- •10.4.2. Необхідні і достатні умови екстремуму
- •10.4.3. Найбільше і найменше значення функції в замкнутій області
10.4.3. Найбільше і найменше значення функції в замкнутій області
Нехай
функція
визначена
і неперервна в обмеженій замкнутій
області
 .
Тоді вона досягає в деяких точках свого
найбільшого
і найменшого
значень (т.3. глобальний екстремум). Ці
значення досягаються функцією в точках,
розташованих усередині області, або в
точках, що лежать на межі області.
.
Тоді вона досягає в деяких точках свого
найбільшого
і найменшого
значень (т.3. глобальний екстремум). Ці
значення досягаються функцією в точках,
розташованих усередині області, або в
точках, що лежать на межі області.
Правило знаходження найбільшого і найменшого значень диференційованої в області функції полягає в наступному:
1. Знайти всі критичні точки функції, що належать і обчислити значення функції в них;
2. Знайти найбільше і найменше значення функції на кінцях області;
3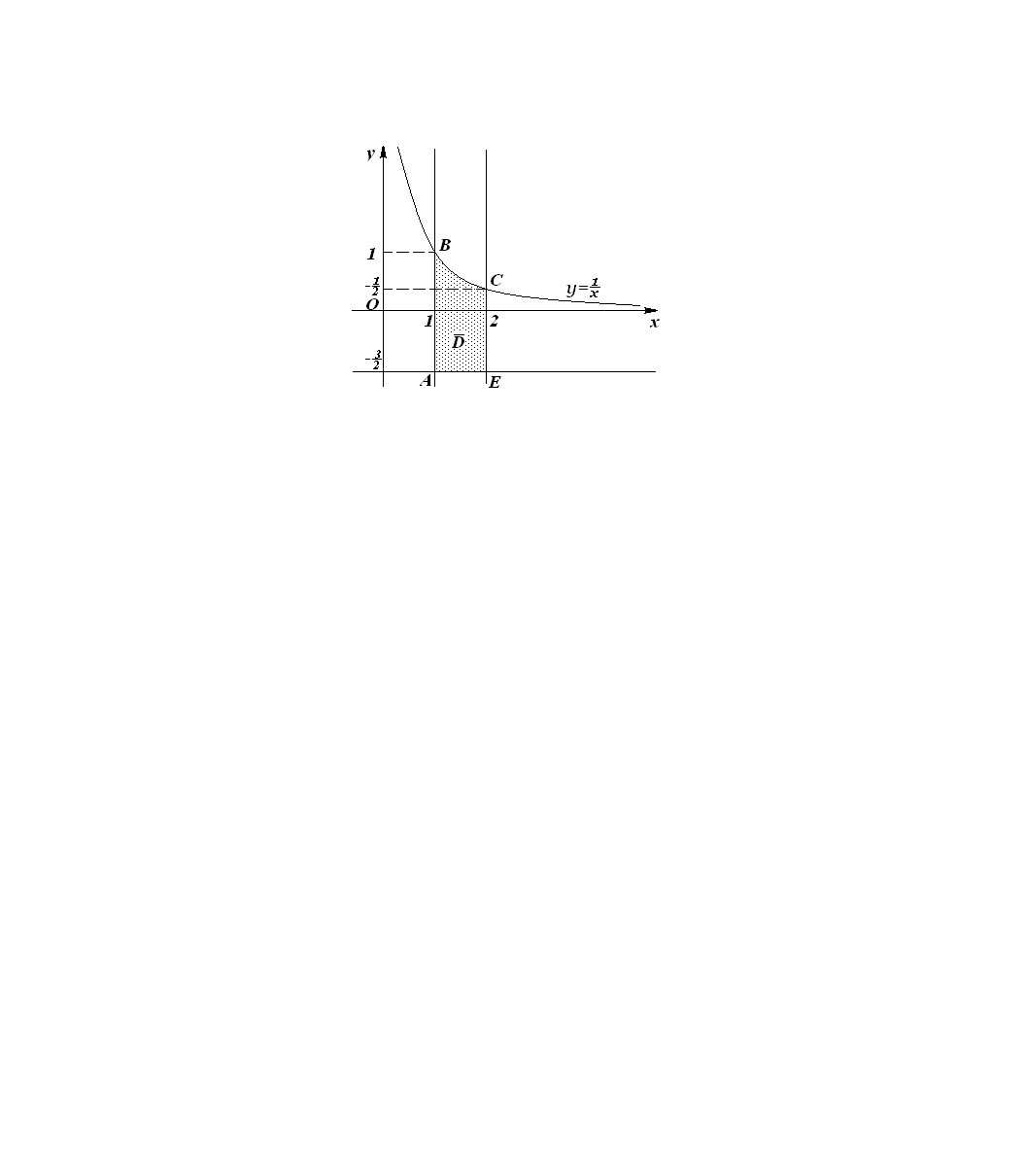 .
Порівняти всі знайдені значення
функції і вибрати з них найбільше
і найменше
.
.
Порівняти всі знайдені значення
функції і вибрати з них найбільше
і найменше
.
Приклад
2.
Знайти щонайбільше і якнайменше
значення функції
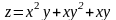 в
замкнутій області, обмеженій лініями:
в
замкнутій області, обмеженій лініями:
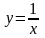 ,
,
,
,
 ,
,
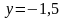 (див. рис. 7).
(див. рис. 7).
Тут
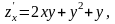

1. Знаходимо всі критичні точки:
Рис. 7
Розв’язком
системи є точки
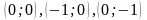
Жодна із знайдених точок не належить області .
2.
Досліджуємо функцію
на
межі області, що складається з ділянок
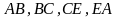 (рис. 212).
(рис. 212).
На
ділянці
 :
,
:
,
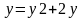 ,
де
,
де
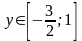
 ,
,
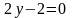 ,
,
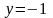 .
Значення функції
.
Значення функції
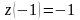 ,
,
 .
.
На
ділянці
 :
:
,
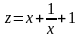 ,
де
,
де
 ,
,

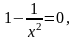
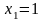 ,
,
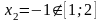 .
Значення функції
,
.
Значення функції
,
 .
.
На
ділянці
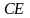 :
,
:
,

 ;
;
 ;
;
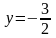 .
Значення функції
.
Значення функції

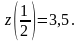
На
ділянці
 :
:

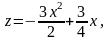 ,
,
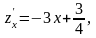

 Значення
функції
Значення
функції

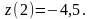
3.
Порівнюючи отримані результати, маємо:
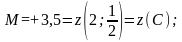 а
а