
- •Функції багатьох змінних
- •Тема 10.1. Функції двох змінних.
- •Тема 10.2. Похідні і диференціали функцій декількох змінних.
- •Тема 10.3. Дотична площина і нормаль до поверхні.
- •Тема 10.4. Екстремум функції двох змінних.
- •10.4.1. Основні поняття.
- •10.1. Функції двох змінних
- •10.1.1. Основні поняття
- •10.1.2. Границя функції
- •10.1.3. Неперервність функції двох змінних
- •10.1.4. Властивості функцій, неперервних в обмеженій замкненій області
- •10.2. Похідні і диференціали функцій декількох змінних
- •10.2.1. Частинні похідні першого порядку та їх геометричний зміст
- •Геометричний зміст частинних похідних функції двох змінних
- •10.2.2. Частинні похідні вищих порядків
- •10.2.3. Диференційовність і повний диференціал функції.
- •10.2.4. Застосування повного диференціала для наближених обчислень
- •10.2.5. Диференціали вищих порядків
- •10.2.6. Похідна складної функції. Повна похідна
- •10.2.7. Інваріантність форми повного диференціала
- •10.2.8. Диференціювання неявної функції
- •10.3. Дотична площина і нормаль до поверхні
- •10.4. Екстремум функції двох змінних
- •10.4.1. Основні поняття
- •10.4.2. Необхідні і достатні умови екстремуму
- •10.4.3. Найбільше і найменше значення функції в замкнутій області
10.1.4. Властивості функцій, неперервних в обмеженій замкненій області
Приведемо властивості функцій, неперервних в обмеженій замкнутій області (вони аналогічні властивостям неперервних на відрізку функцій однієї змінної – див. п. 19.5). Заздалегідь уточнимо поняття області.
Областю називається множина точок площини, що володіють властивостями відкритості і зв'язності.
Властивість відкритості: кожна точка належить їй разом з деяким околом цієї точки.
Властивість зв'язності: будь-які дві точки області можна з'єднати неперервною лінією, що цілком лежить в цій області.
Точка називається межовою точкою області , якщо в будь-якому околі її лежать як точки цієї області так і точки що їй не належать.
Сукупність межових точок області називається межею .
Область з приєднаною до неї межею називається замкнутою областю.
Область називається обмеженою, якщо всі її точки належать деякому кругу радіуса . Інакше область називається необмеженою. Прикладом необмеженої області може служити множина точок першого координатного кута, а прикладом обмеженої – окіл точки .
Теорема
10.1.
Якщо
функція
 неперервна
в обмеженій замкнутій області, то вона
в цій області:
неперервна
в обмеженій замкнутій області, то вона
в цій області:
а)
обмежена, тобто існує таке число
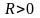 ,
що для всіх точок
,
що для всіх точок
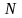 в цій області виконується нерівність
в цій області виконується нерівність
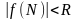 ;
;
б) має
точки, в яких приймає найменше
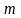 і найбільше
значення;
і найбільше
значення;
в) приймає хоча б в одній точці області будь-яке чисельне значення, розміщене між і .
Теорема дається без доведення.
10.2. Похідні і диференціали функцій декількох змінних
10.2.1. Частинні похідні першого порядку та їх геометричний зміст
Нечай
задана функція
.
Оскільки
і
–
незалежні
змінні, то одна з них може змінюватися,
а інша зберігати своє значення. Дамо
незалежній змінній
приріст
,
зберігаючи значення
незмінним. Тоді
отримає приріст, який називається
частинним
приростом
по
і позначається
 .
Отже
.
Отже
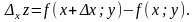 Аналогічно
одержуємо частинний приріст
по
:
Аналогічно
одержуємо частинний приріст
по
:
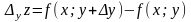
Повний
приріст функції
визначається рівністю
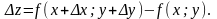
Якщо
існує границя
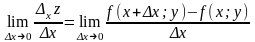 ,
то
вона називається частинною
похідною функції
в
точці
по
змінній
і позначається одним із символів:
,
то
вона називається частинною
похідною функції
в
точці
по
змінній
і позначається одним із символів:

Частинні похідні по в точці звичайно позначають символами

Аналогічно визначається і позначається частинна похідна від по змінні :
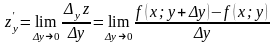
Таким чином, частинна похідна функції декількох (двох, трьох і більше) змінних визначається як похідна функції однієї з цих змінних за умови постійності значень решти незалежних змінних. Тому частинні похідні функції знаходять по формулах і правилах обчислення похідних функції однієї змінної (при цьому відповідно або вважається сталою величиною).
Приклад
1.
Знайти частинні похідні функції
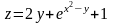
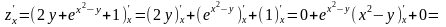
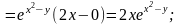
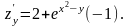
Геометричний зміст частинних похідних функції двох змінних
Г рафіком
функції
є деяка поверхня (див.
п. 12.1). Графіком функції
рафіком
функції
є деяка поверхня (див.
п. 12.1). Графіком функції
 є
перетин
цієї поверхні з площиною
є
перетин
цієї поверхні з площиною
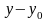 .
Виходячи з геометричного змісту похідної
для функції однієї змінної (див. п. 20.2),
заключаємо, що
.
Виходячи з геометричного змісту похідної
для функції однієї змінної (див. п. 20.2),
заключаємо, що
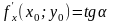 ,
де
,
де
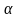 - кут між віссю
- кут між віссю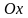 і
дотичною, проведеною
до
кривої
в
точці
і
дотичною, проведеною
до
кривої
в
точці
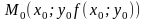 (див. рис. 3).
Аналогічно
(див. рис. 3).
Аналогічно
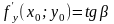 .
.
Рис.3
