Глава 5. Интеграл Фурье. Преобразование Фурье
5.1. Определение интеграла Фурье
Пусть
функция
абсолютно
интегрируема на всей действительной
оси, то есть
сходится.
Определение 1. Интеграл
,
где
называется интегралом Фурье функции .
Интеграл Фурье имеет другую форму записи
Теорема 1. (Достаточное условие представления функции интегралом Фурье).
Пусть
абсолютно
интегрируема на
и
кусочно-гладкая на любом конечном
отрезке. Тогда интеграл Фурье сходится
в каждой точке, и имеет место равенство
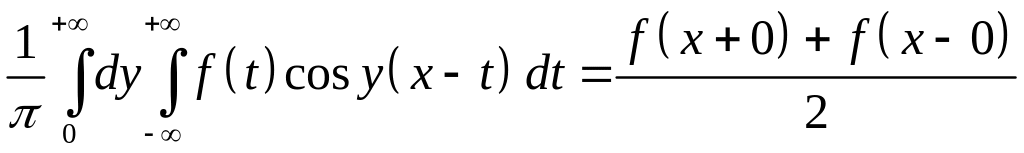
Эта формула называется формулой Фурье.
5.2. Интеграл Фурье для четной и нечетной функции
Свойства четной и нечетной функции, как и в случае с рядами Фурье, позволяет упростить форму записи интеграла Фурье.
Пусть
-четная
функция, удовлетворяющая условиям
представления интегралом Фурье. Тогда
,
,
а
интеграл будет иметь вид
.
Если -нечетная функция, то
,
,
а интеграл запишется как
.
5.3. Комплексная форма записи интеграла Фурье
Если
-
абсолютно интегрируема и кусочно-гладкая
на любом конечном отрезке, то, используя
формулу Эйлера
,
получим
комплексную форму интеграла Фурье
,
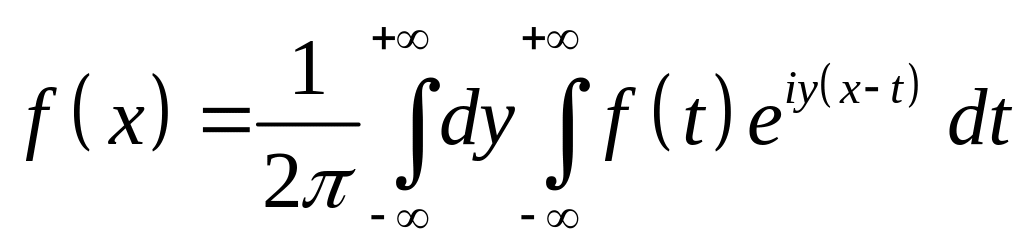при этом внешний интеграл берется в смысле главного значения.
Определение 2. Пусть функция -интегрируема на любом конечном отрезке. Если существует конечный предел
,
то
он называется главным значением интеграла
и
обозначается буквами
v.p
.
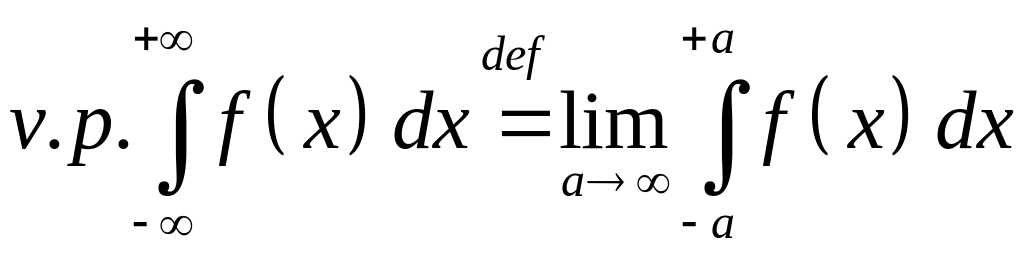5.4. Преобразование Фурье
Определение
3.
Интеграл
,
зависящий
от параметра
,
называется преобразованием
Фурье
функции
.
Другое
обозначение
.
Сходимость
интеграла следует из равенства
и
абсолютной интегрируемости
.
Определение
4.
Интеграл
называется
обратным преобразованием Фурье функции
и обозначается
.
Свойства
преобразования Фурье.
Формула обращения.
.
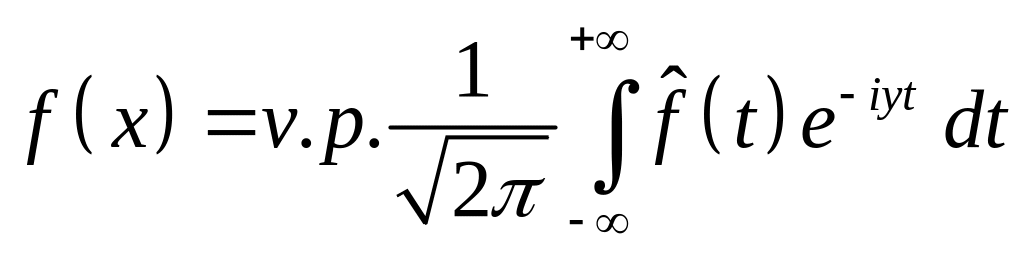Если
непрерывна,
абсолютно интегрируема на
и
кусочно-гладкая
на любом отрезке
,
то
,
то
есть
и
-
взаимно обратные отображения.
Линейность. Пусть для функций и существуют преобразования Фурье. Тогда для любых чисел и существуют преобразования Фурье для функции
,
при этом
.
Преобразование Фурье производной. Если и ее производная до -го порядка включительно непрерывны и абсолютно интегрируемы на , то
.
Производная преобразования Фурье. Если непрерывна на , а функции
абсолютно
интегрируемы на
,
то преобразование Фурье является
раз
дифференцируемым
на
и
.
5.5. Косинус и синус преобразования Фурье
Если функция имеет свойство четности или нечетности, то преобразование Фурье имеет более простую форму.
Пусть -четная и удовлетворяет условиям существования преобразования Фурье. Тогда имеет место формула
,
где
-косинус
преобразование Фурье.
Пусть -нечетная и удовлетворяет условиям существования преобразования Фурье. Тогда имеет место формула
,
где
-синус
преобразование Фурье.
Пример.
Представить
функцию
интегралом
Фурье.
Решение.
Доопределим
функцию
в
точках разрыва
значением
.
Учитывая,
что
-четная,
получим
,
,
.
Полагая , получим интеграл Дирихле
.
Варианты индивидуального задания.
Задание 1. Вычислить несобственный интеграл или установить его расходимость.
1. .
2.
3.
4.
5.
|
6.
7.
8.
9.
10.
|
.
.
.
.
.
.
.
.
.
Задание 2. Исследовать на сходимость несобственные интегралы от знакопостоянных функций.
1.
; 
; 
.
2.
; 
; 
.
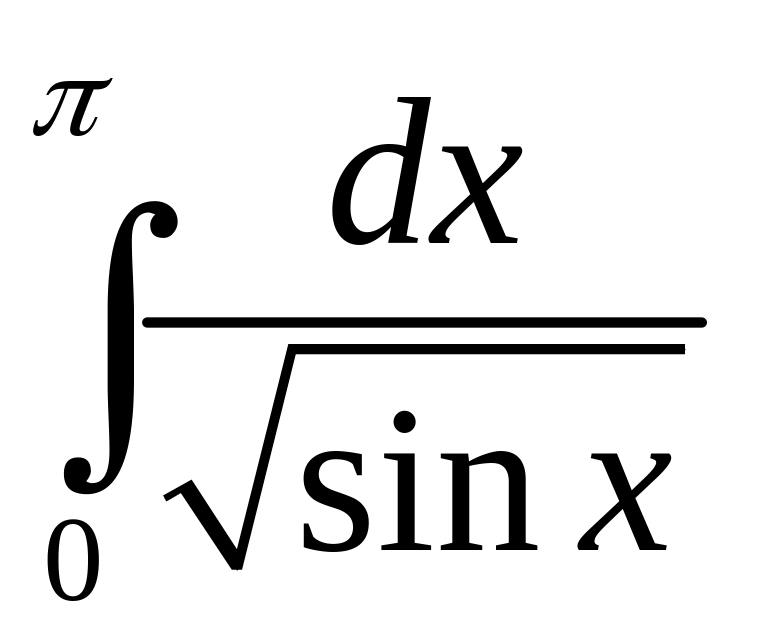3.
; 
; 
.
4.
; 
; 
.
5.
; 
; 
.
6.
; 
; 
.
7.
; 
; 
.
8.
; 
; 
.
9.
; 
; 
.
10.
; 
; 
.
Задание 3. Исследовать, при каких значениях параметров сходится интеграл
1.
2.
3.
4.
5.
|
6.
7.
8.
9.
10.
|
Задание 4. Исследовать несобственный интеграл на абсолютную и условную сходимость.
1.
2.
3.
4.
5.
|
6.
7.
8.
9.
10.
|
.
.
.
.
.
.
.
.
.
.
Задание 5. С помощью Эйлеровых интегралов найти следующие интегралы.
1.
2.
3.
4.
5.
|
6.
7.
8.
9.
10.
|
.
.
.
.
.
.
.
.
.
.
Задание 6. Разложить в ряд Фурье функции. Нарисовать график функции и суммы ряда Фурье.
1.
Пользуясь
разложением, найти
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
по синусам.
9.
по косинусам.
10.
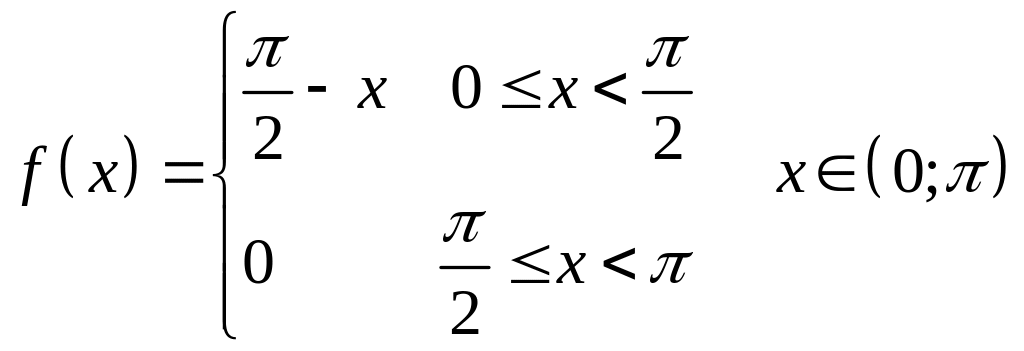по косинусам.
Задание 7. Представить функцию интегралом Фурье.
1.
.
2.
.
3.
.
4.
.
5.
.
Найти преобразование Фурье функции и восстановить по нему данную функцию.
6.
.
7. .
8.
.
9. Представить интегралом Фурье функцию по синусам
.
10. Найти преобразование Фурье функции
.
Образец контрольной работы по теме «Несобственный интеграл»
1. Исследовать на сходимость:
а)
; б)
; в)
; г)
.
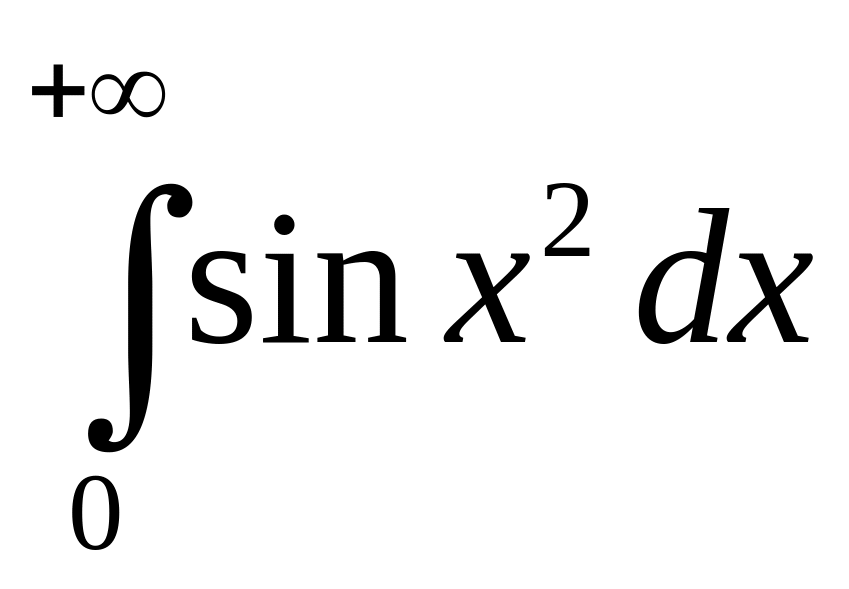2.
Найти
,
если
.
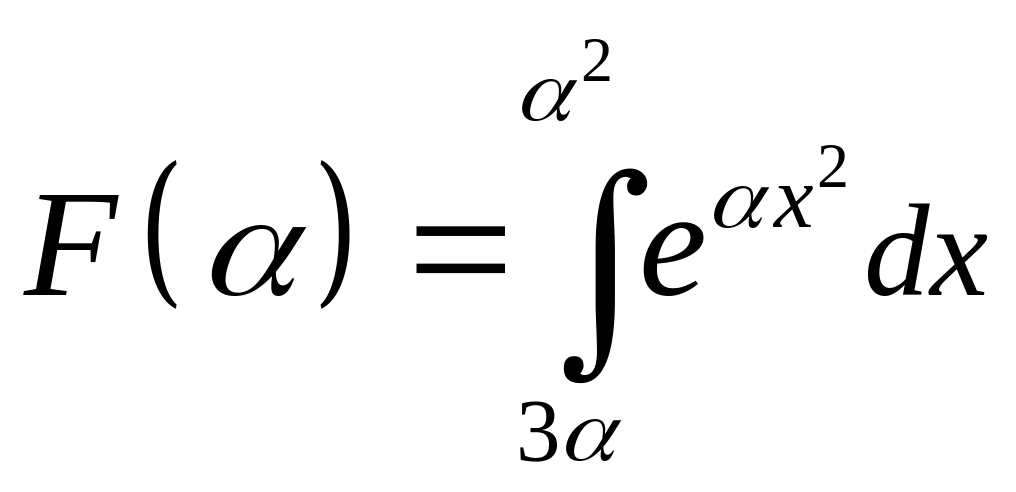3. С помощью дифференцирования по параметру вычислить
.
4. Исследовать равномерную сходимость
на
множестве
.
5. Используя Эйлеровы интегралы, вычислить
.
Учебное издание
Попова Галина Андреевна
Гридасова Ирина Васильевна
Пайков Владимир Иванович
Несобственные интегралы и ряды Фурье
Редактор Р.В. Щадько
План изд. 2010 г., поз. № 18
Подписано в печать 2010 г. Формат 60/84.1/16. Бумага офсет. Печать офсет. Усл.-печ. л. . Усл.-изд. л. . Тираж экз. Заказ № .
Издательство: Донецкий национальный университет, 83001, Донецк-01, Университетская, 24.
Напечатано: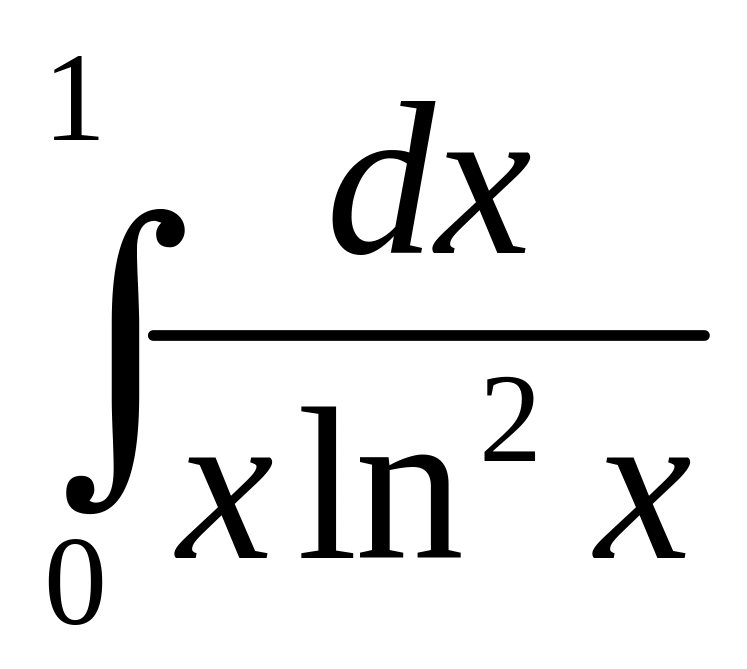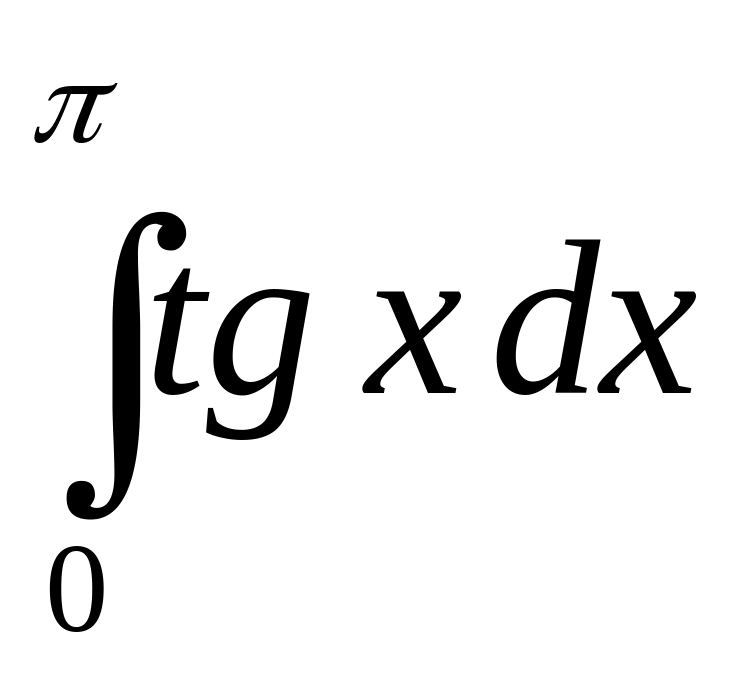
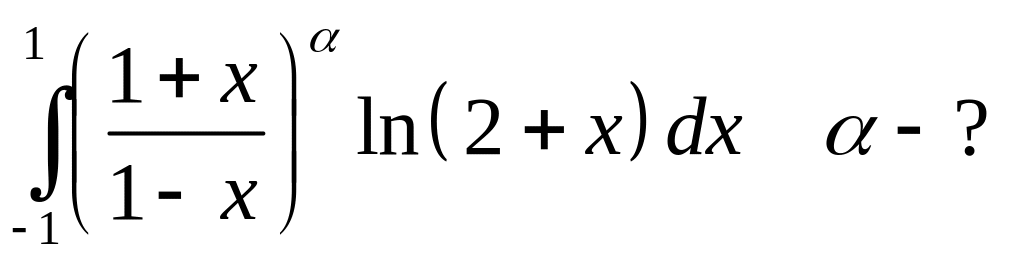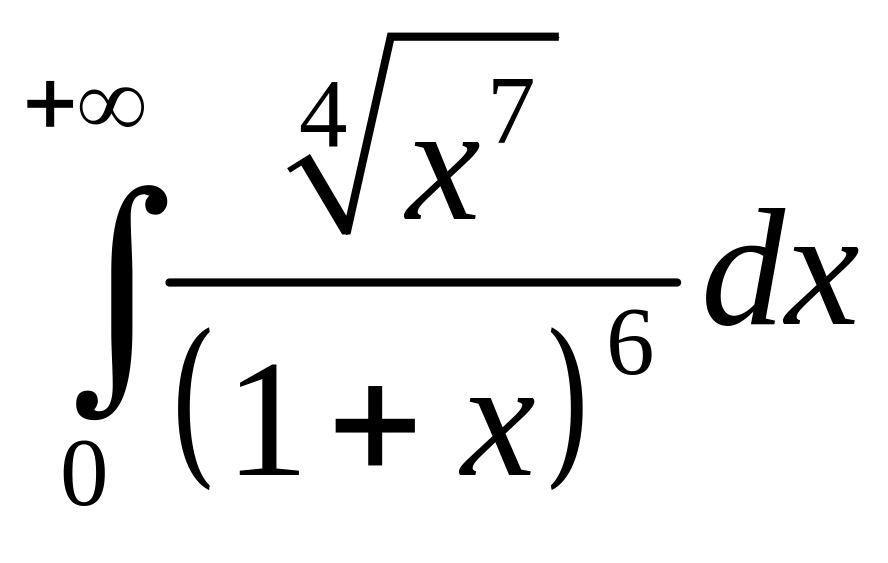