4.5. Разложение в ряд Фурье только по синусам или только по косинусам

Начнем с простого замечания: если заданная на отрезке интегрируемая функция является нечетной, то есть для всех выполняется равенство , то .

Для четной функции справедливо .

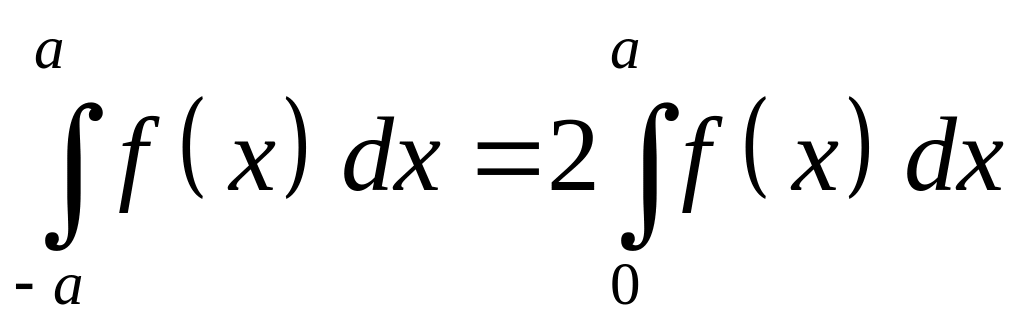Напомним некоторые свойства четных и нечетных функций на :

1. Произведение двух четных или двух нечетных функций есть функция четная;

2. Произведение четной и нечетной функций есть нечетная функция.

Утверждение. Пусть определена и интегрируема на , а -ее коэффициенты Фурье. Тогда

1. если -нечетная, то

, а ряд Фурье имеет вид .

2. если - четная, то

, а ряд Фурье имеет вид .

Допустим, что функция задана на отрезке . Если мы хотим найти разложение на этом отрезке в ряд Фурье, то сначала продолжим на симметричный промежуток произвольным образом, а потом воспользуемся формулами для коэффициентов Фурье.

Если продолжить функцию четным образом, то получим разложение только по косинусам, а если продолжить нечетным образом, то – только по синусам. При этом в первом случае продолженная функция будет иметь вид

,

а во втором случае

4.6. Разложение в ряд Фурье функции, заданной на произвольном промежутке

Пусть задана на отрезке , и на этом отрезке она кусочно-гладкая. Рассмотрим периодическую кусочно-гладкую функцию с периодом

,

которая совпадает с на , а -произвольная кусочно-гладкая функция.

Таким образом, была продолжена на симметричный отрезок. Теперь для существует разложение в ряд Фурье. Сумма этого ряда совпадает с во всех точках непрерывности отрезка , то есть функция разложена в ряд Фурье на .

Алгоритм разложения функции в тригонометрический ряд Фурье:

1. выяснить формально ряд Фурье по заданию функции;

2. найти коэффициенты ряда Фурье;

3. используя теорему о достаточном условии сходимости ряда Фурье, найти сумму ряда, построить график и . Выяснить, в каких точках совпадает с .

4.7. Контрольные вопросы и задания.

1. Какая функция называется периодической? Является ли функция Дирихле периодической? Чему равен период? Имеет ли эта функция основной период?

2. Что такое тригонометрический ряд?

3. Какой тригонометрический ряд называется рядом Фурье?

4. Являются ли тригонометрические ряды и рядами Фурье?

5. Сформулировать достаточные условия поточечной сходимости ряда Фурье.

6. Записать равенство Парсеваля и неравенство Бесселя для тригонометрического ряда Фурье.

7. Какой вид имеет ряд Фурье для нечетной интегрируемой функции?

8. Какой вид имеет ряд Фурье для -периодической функции?

4.8. Образцы решения типовых задач

При нахождении коэффициентов Фурье полезно помнить:

.

Пример 1. Разложить функцию в ряд Фурье на интервале . Построить график суммы ряда Фурье. Вычислить суммы получающихся рядов, полагая .

Построим график данной функции:

Продолжим данную функцию периодически с периодом на всю прямую.

Построим график суммы ряда Фурье

Найдём коэффициенты ряда Фурье. Так как нечётная на

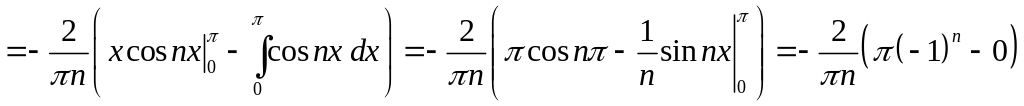
Итак, .

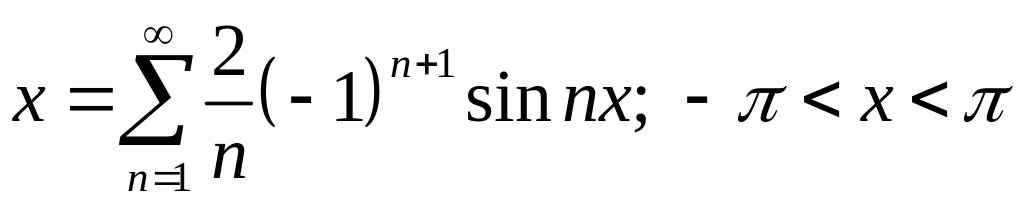Используя полученное разложение с учётом вида графика суммы ряда Фурье, из которого видно, к чему сходится ряд в точках разрыва, найдём суммы некоторых числовых рядов.

При получим .

При получим

.

При получим

.

Пример 2. Разложить в ряд Фурье по косинусам функцию 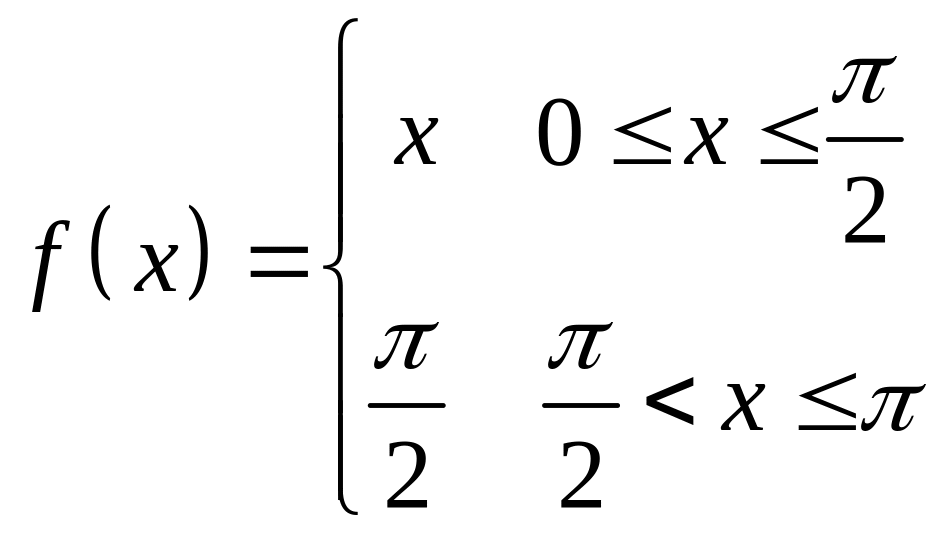(полупериод функции равен )

Изобразим график заданной функции

Продолжим функцию чётным образом на промежутке , тогда коэффициенты .

Продолжим полученную функцию с периодом на всю прямую. Так как продолжение будет непрерывной функцией, то для график суммы ряда Фурье совпадает с графиком продолженной функции

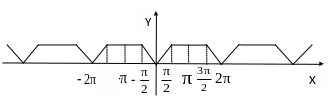
Вычислим коэффициенты ряда Фурье

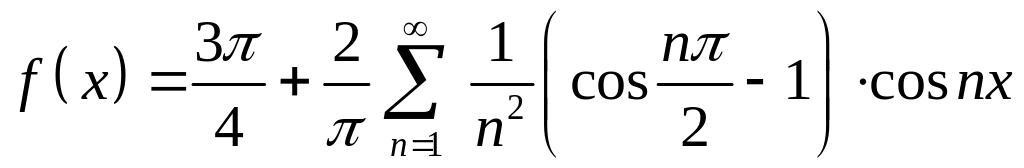
при .

Пример 3. Разложить в ряд Фурье по синусам функцию (полупериод функции равен )

Разложение функции в ряд по синусам - это ряд Фурье нечётного продолжения функции с промежутка на промежуток .

Изобразим график суммы ряда Фурье

Имеем .