Глава 4 . Ряды Фурье

4.1. Периодические функции и их свойства

Определение 1. Функция называется периодической на множестве , если существует константа такая, что для любого и и выполнено равенство

).

Константа называется периодом функции

Определение 2. Наименьшее положительное значение называется основным (или наименьшим) периодом периодической функции. Свойства периодических функций:

1. Если -период функции, то так же период, где .

2. Если периодическая с периодом , то при любом имеет период .

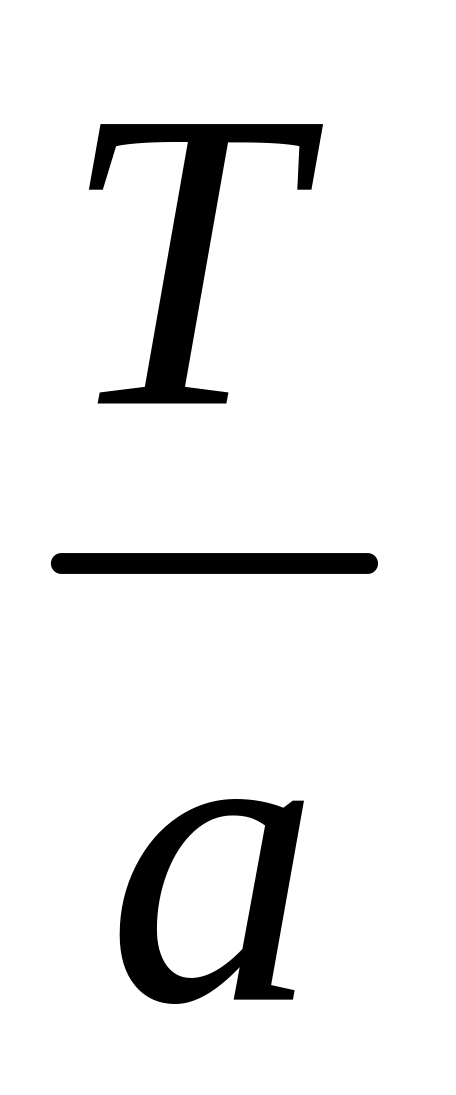3. Если -(основной) период функции , -(основной) период функции , ... , -(основной) период функции , то -периодическая с основным периодом = НОК (наименьшее общее кратное).

4. Если функция периодическая с периодом , то

при условии .

4.2. Тригонометрическая система

Система функции называется основной тригонометрической системой.

Указанная система функций обладает свойством ортогональности на отрезке :

Отметим также следующие равенства:

Пусть интегрируема на отрезке .

Числа

называются коэффициентами Фурье функции по основной тригонометрической системе.

Определение 3. Тригонометрический ряд

,

где -коэффициенты Фурье функции , называется рядом Фурье функции .

В частности, если функция четная, то ее ряд Фурье имеет вид

Ряд Фурье нечетной функции имеет вид .

Определение 4. Функция называется кусочно-непрерывной на отрезке , если она непрерывна в каждой точке за исключением, быть может, конечного числа точек, где она имеет разрывы первого рода.

Определение 5. Функция называется кусочно-дифференцируе-мой на отрезке , если эта функция кусочно-непрерывна и имеет непрерывную производную на этом отрезке за исключением, быть может, конечного числа точек, в каждой из которых производная имеет конечные односторонние предельные значения , .

4.3. Достаточные условия поточечной сходимости ряда Фурье

Теорема 1. Пусть кусочно-дифференцируемая на отрезке функция периодически с периодом продолжена на всю бесконечную прямую. Тогда тригонометрический ряд Фурье функции сходится в каждой точке к значению .

Теорема 2. Если для непрерывной и кусочно-дифференцируемой на функции выполняется , то ее тригонометрический ряд Фурье сходится равномерно на этом отрезке, и сумма ряда равна в каждой точке .

Теорема 3. (О единственности разложения в ряд Фурье). Пусть и ряд, стоящий в правой части этого равенства, сходится равномерно на . Тогда -коэффициенты Фурье функции . Иными словами, всякий равномерно сходящийся тригонометрический ряд является рядом Фурье своей суммы.

Утверждение. Для тригонометрического ряда Фурье функции справедливо неравенство Бесселя

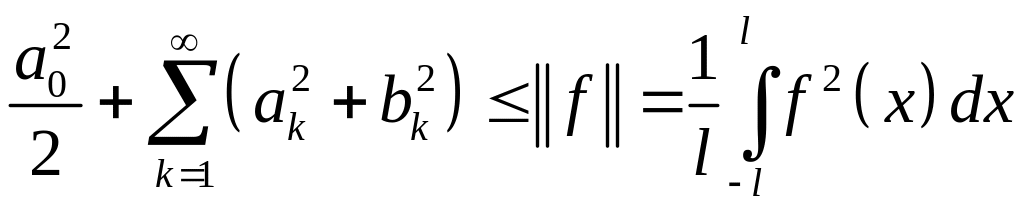
и равенство Парсеваля

.

Замечание. Из неравенства Бесселя следует, что ряд ,

составленный из квадратов коэффициентов Фурье функции , сходится.

4.4. Почленное дифференцирование и интегрирование ряда Фурье

Из теории функциональных рядов известно, насколько важно уметь дифференцировать и интегрировать функциональные ряды почленно. Известно также, что для степенных рядов нет необходимости применять общие теоремы функциональных рядов, поскольку на интервале сходимости их можно как дифференцировать, так и интегрировать. Похожая ситуация имеет место для рядов Фурье.

Теорема 4. (О дифференцировании). Пусть

1. непрерывна на ;

2. на концах отрезка принимает равные значения ;

3. кусочно-дифференцируема на .

Тогда ряд Фурье для производной можно получить путем формального почленного дифференцирования ряда Фурье функции . То есть, если

, то

.

Теорема 5. (Об интегрировании). Пусть непрерывна на и ряд -ряд Фурье . Тогда имеет место равенство

.

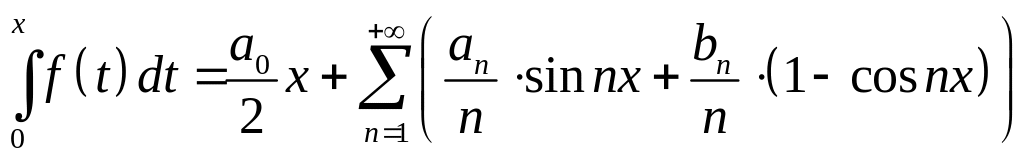При этом ряд, стоящий в правой части последнего равенства, сходится равномерно на .