
- •Глава 1. Несобственные интегралы
- •1.1. Понятие несобственного интеграла от неограниченной функции
- •1.2. Понятие несобственного интеграла по неограниченному промежутку
- •1.3. Формулы интегрального исчисления для несобственных интегралов
- •1.4. Критерий Коши сходимости несобственных интегралов.
- •1.4. Критерий Коши сходимости несобственных интегралов
- •1.5. Признаки сходимости интегралов от неотрицательных функций (признаки сравнения)
- •1.6. Абсолютная и условная сходимость несобственных интегралов. Признаки Абеля и Дирихле
- •1.7. Контрольные вопросы и задания.
- •1.8 Примеры решения типовых задач.
- •Глава 2. Собственные интегралы, зависящие от параметра
- •Глава 3. Несобственные интегралы, зависящие от параметра
- •3.1. Сходимость. Равномерная сходимость
- •3.2. Достаточные признаки равномерной сходимости
- •3.5. Контрольные вопросы и задания
- •3.6. Образцы решения типовых задач
- •Глава 4 . Ряды Фурье
- •4.1. Периодические функции и их свойства
- •4.2. Тригонометрическая система
- •4.3. Достаточные условия поточечной сходимости ряда Фурье
- •4.4. Почленное дифференцирование и интегрирование ряда Фурье
- •4.5. Разложение в ряд Фурье только по синусам или только по косинусам
- •4.6. Разложение в ряд Фурье функции, заданной на произвольном промежутке
- •4.7. Контрольные вопросы и задания.
- •4.8. Образцы решения типовых задач
- •Глава 5. Интеграл Фурье. Преобразование Фурье
- •5.1. Определение интеграла Фурье
- •5.2. Интеграл Фурье для четной и нечетной функции
- •5.3. Комплексная форма записи интеграла Фурье
- •5.4. Преобразование Фурье
- •5.5. Косинус и синус преобразования Фурье
1.8 Примеры решения типовых задач.
Пример
1.
Исследовать сходимость интеграла
 .
.
Функция
![]() на
промежутке
на
промежутке
![]() имеет
одну особую точку
.
Воспользуемся
определением несобственного интеграла
имеет
одну особую точку
.
Воспользуемся
определением несобственного интеграла
 -
не
существует
-
не
существует
![]() расходится.
расходится.
Пример
2.
Исследовать сходимость и вычислить ( в
случае сходимости ) интеграл
 .
.

Пример
3.
Исследовать сходимость
 .
.
Заметим,
что так как подынтегральная функция
рациональна, то её первообразная
выражается элементарной функцией. Но
вычисление первообразной здесь громоздко
и для ответа на вопрос воспользуемся
не определением несобственного интеграла,
а признаком сравнения, так как
подынтегральная функция положительна.
Так как особой точкой является
,
интеграл
![]() сходится
и
сходится
и
 ,
то
в силу признака сравнения исходный
интеграл сходится.
,
то
в силу признака сравнения исходный
интеграл сходится.
Пример
4.
Исследовать сходимость интеграла
 .
.
Функция
 имеет
на промежутке интегрирования две особые
точки
имеет
на промежутке интегрирования две особые
точки
![]() и
и
![]() .
Следовательно
необходимо рассмотреть сходимость
каждого из
интегралов
.
Следовательно
необходимо рассмотреть сходимость
каждого из
интегралов
 и
и
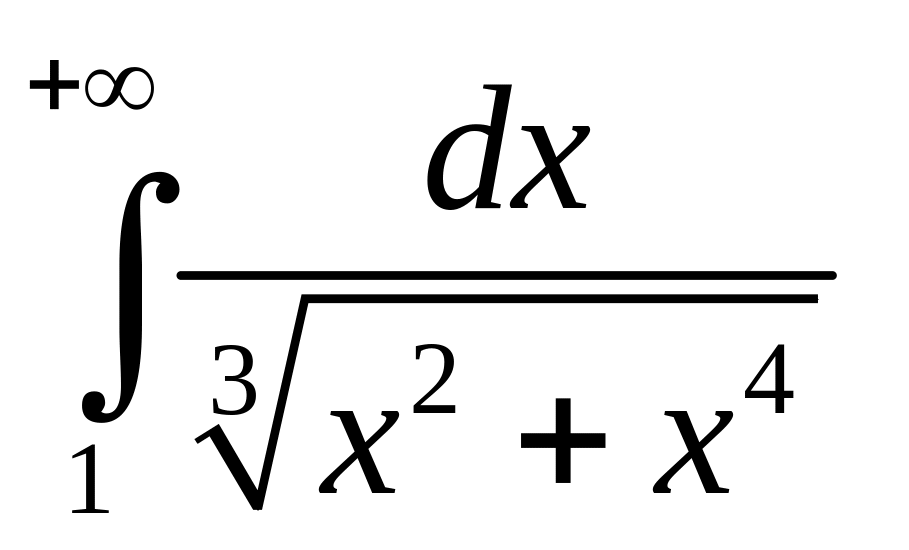 .
Воспользуемся
признаком сравнения
.
Воспользуемся
признаком сравнения
 ;
;
 .
Так
как оба интеграла
.
Так
как оба интеграла
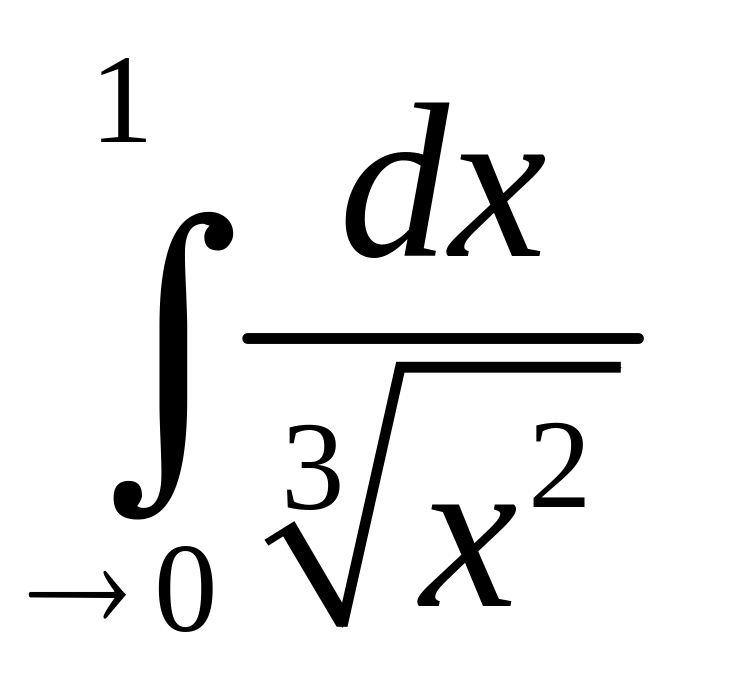 и
и
 сходятся,
то сходится и исходный.
сходятся,
то сходится и исходный.
Пример
5.
Исследовать сходимость интеграла
 .
.
Подынтегральная
функция имеет на промежутке
![]() две
особые точки
и
две
особые точки
и
![]() .
Разобьем
наш интеграл на два
.
Разобьем
наш интеграл на два
 .
Так
как
.
Так
как
 и
и
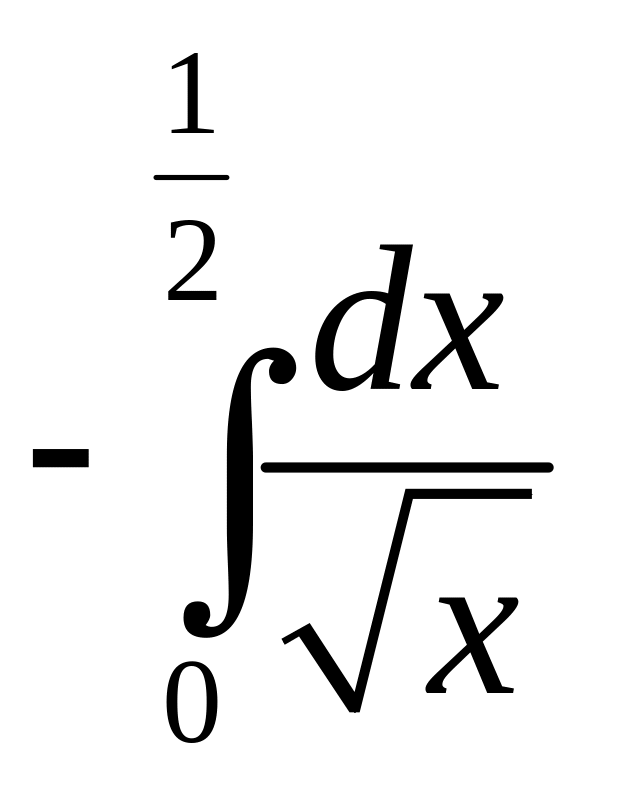 сходится,
то сходится
сходится,
то сходится
 .
Так
как
.
Так
как
 и
и
 расходится,
то
расходится,
то
 расходится.
Следовательно, исходный интеграл
расходится.
расходится.
Следовательно, исходный интеграл
расходится.
Пример
6.
Исследовать сходимость интеграла
 .
.
Особая
точка
.
Так
как
![]() при
,
то
при достаточно малых
при
,
то
при достаточно малых
![]() имеет
место оценка
имеет
место оценка
![]()
 .
Подберём
так,
чтобы
.
Подберём
так,
чтобы
 .
Тогда
интеграл от «большей» функции
будет
сходится. По признаку сравнения
исходный
интеграл сходится.
.
Тогда
интеграл от «большей» функции
будет
сходится. По признаку сравнения
исходный
интеграл сходится.
Пример
7.
Исследовать абсолютную или условную
сходимость интеграла
 .
.
Функция
![]() имеет
на
одну
особую точку
,
является
знакопроизвольной. Исследуем сходимость
интеграла по признаку Дирихле.
имеет
на
одну
особую точку
,
является
знакопроизвольной. Исследуем сходимость
интеграла по признаку Дирихле.
 -ограничена
на
,
функция
-ограничена
на
,
функция
![]() -монотонно
убывает слева в точке
,
так
как
-монотонно
убывает слева в точке
,
так
как
 при
при
![]() и
и
![]() .
Итак,
в силу признака Дирихле, интеграл
сходится.
.
Итак,
в силу признака Дирихле, интеграл
сходится.
Для
исследования абсолютной сходимости
данного интеграла воспользуемся оценкой
![]() .
Имеем
.
Имеем
 .
.
Дословно
повторяя приведённые выше рассуждения,
получим, что интеграл
 сходится. Так как
сходится. Так как
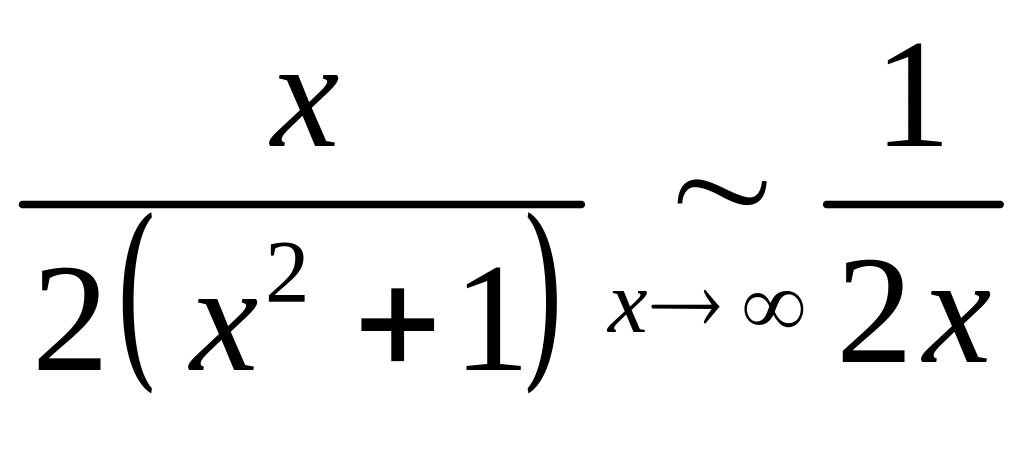 ,
то
по признаку сравнения
,
то
по признаку сравнения
 расходится. Следовательно, интеграл
расходится. Следовательно, интеграл расходится
и
исходный интеграл сходится условно.
расходится
и
исходный интеграл сходится условно.
Пример 8. Исследовать на сходимость несобственные интегралы
а) сходится.
сходится.
б) расходится.
расходится.
в) сходится.
сходится.
г) ,
(где
,
(где
![]() ,
так
как
,
так
как
![]() при
достаточно большом значении
при
достаточно большом значении
![]() верна
оценка
верна
оценка
![]() )
)
Подберём
так,
чтобы
![]() (тогда интеграл от «большей» функции
будет
сходящимся). При
(тогда интеграл от «большей» функции
будет
сходящимся). При
 данный
интеграл сходится.
данный
интеграл сходится.
д) и интеграл от «меньшей» функции
расходится
исходный интеграл расходится.
и интеграл от «меньшей» функции
расходится
исходный интеграл расходится.
е)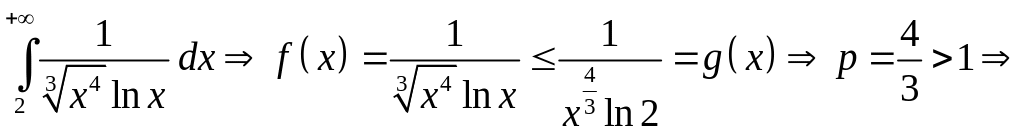 сходится.
сходится.
«Большая» функция , интеграл от неё сходится исходный интеграл сходится.
ж) .
Подберём
так,
чтобы
.
Подберём
так,
чтобы
![]() (тогда
интеграл от «меньшей» функции
будет
расходящимся). При
(тогда
интеграл от «меньшей» функции
будет
расходящимся). При
![]() данный интеграл расходится.
данный интеграл расходится.
з) .
Особая точка
,
так
как
.
Особая точка
,
так
как
 .
.
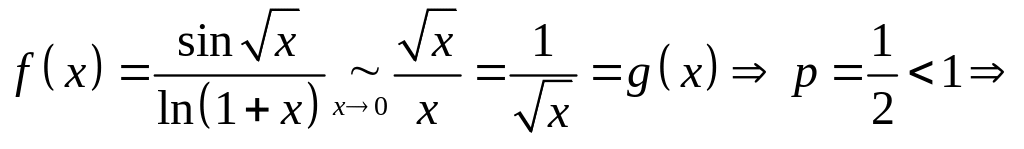 интеграл
сходится.
интеграл
сходится.
и) .
Исследуем на сходимость каждый интеграл.
.
Исследуем на сходимость каждый интеграл.
 первый
интеграл сходится.
первый
интеграл сходится.
 .
Исследуем
на сходимость интеграл
.
Исследуем
на сходимость интеграл
 .
Сделаем
замену в интеграле
.
Сделаем
замену в интеграле
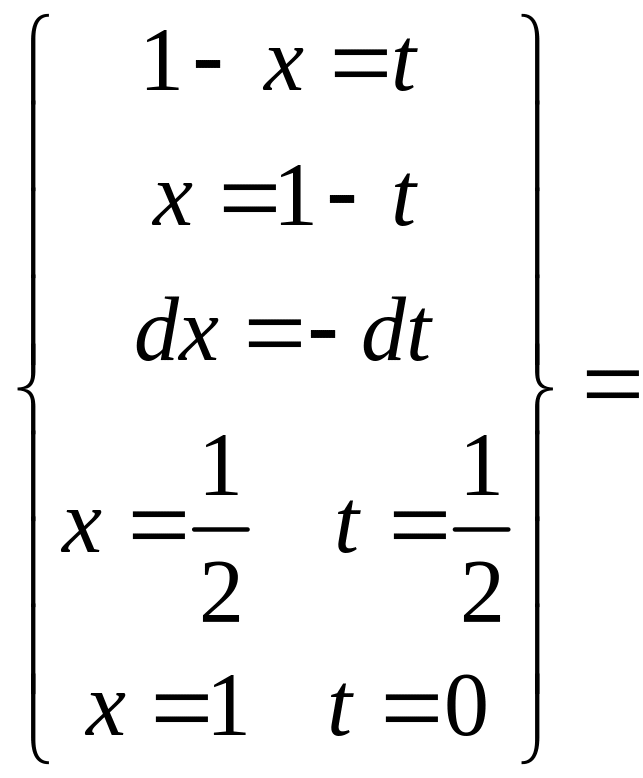
 второй
интеграл сходится.
второй
интеграл сходится.
Следовательно, исходный интеграл сходится.
