4.2. Взаимная индукция. Энергия магнитного поля. Уравнения Максвелла
Основные формулы
эдс взаимной индукции
,
(47)
где – взаимная индуктивность контуров)
Взаимная индуктивность двух катушек, намотанных на общий сердечник,
,
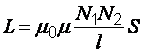(48)
где
–
длина сердечника по средней линии;
–
площадь поперечного сечения сердечника;
–
число витков первой и второй катушек.
Коэффициент трансформации двухобмоточного тансформатора
,
(49)
где
–
эдс индукции в обмотках трансформатора.
Энергия магнитного поля
,
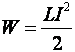(50)
где – индуктивность замкнутого контура; – сила тока.
Объёмная плотность энергии однородного магнитного поля
,
(51)
где – энергия однородного магнитного поля; – объём соленоида, – магнитная индукция, – напряженность магнитного поля.
Плотность тока смещения
,
(52)
где
–
электрическое смещение;
–
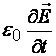плотность тока смещения в вакууме;
–
плотность тока поляризации.
Обобщенная теорема о циркуляции вектора
,
(53)
где
–
плотность тока проводимости;
–
плотность тока смещения;
–
поверхность, охватываемая замкнутым
контуром
.
Уравнения Максвелла в интегральной форме:
;
(54 а)
;
(54 б)
;
(54 в)
.
(54 г)
(54)
Методические рекомендации
1.
Взаимная индукция – частный случай
электромагнитной индукции, заключается
в возникновении эдс в одном из контуров
при изменении силы тока в другом. Поэтому
эдс индукции определяется по закону
Фарадея (47). В этой формуле
–
взаимная индуктивность контуров.
Справедливо заметить, что нужно говорить
о взаимной индуктивности каждого контура
.
Но при отсутствии ферромагнетиков
.
Это свойство принято называть теоремой
взаимности. Смысл этой теоремы заключается
в том, что магнитный поток сквозь контур
1, созданный током в контуре 2, равен
магнитному потоку сквозь контур 2,
созданный таким же током в контуре 1.
Это обстоятельство очень часто позволяет
сильно упрощать решение задач с
нахождением магнитных потоков.
При
наличие ферромагнетиков теорема
взаимности перестает выполняться. В
этом случае при вычислении магнитных
потоков
и
в
контурах нужно учитывать, что
и
разные
(они зависят от
и
),
поэтому
и
не
совпадают.
2. В отличие от индуктивности , которая является величиной положительной, взаимная индуктивность – величина алгебраическая (и может быть равна нулю).
Положительные
направления для токов (и эдс) в обоих
случаях можно выбрать произвольно.
Когда эти направления выбраны, то
величину
мы
считаем положительной ( 3. Формула (50) позволяет определить энергию магнитного поля контура с индуктивностью , по которому течет ток , в отсутствии ферромагнетика. Она выражает магнитную энергию тока через индуктивность и силу тока. Но её можно также выразить через |
|
),
если при положительных токах в обоих
контурах они «подмагничивают» друг
друга. В противоположном случае
(рис.
50).
характеристики
магнитного поля: магнитную индукцию
и
напряженность поля
.
Эта формула
справедлива
для однородного поля, заполняющего
объём
.
Однако в общей теории показывается, что
энергию
можно
выразить через
и
в
любом случае (но при отсутствии
ферромагнетиков) по формуле
.
Формула (51) относится только к пара- и диамагнетикам. К ферромагнетикам она не применима.
Используя
формулу (50) и
,
можно определить индуктивность
.
4.
Магнитная энергия двух контуров с током
определяется соотношением
,
где
и
–
собственная энергия 1 и 2 контуров;
–
взаимная энергия обоих токов.
Взаимная энергия токов – величина алгебраическая, в отличие от собственных энергий токов.
5. Энергетический метод является наиболее общим методом определения сил в магнитном поле. В этом методе используется выражение для энергии магнитного поля.
В случае системы из двух контуров с токами и работа источников тока против эдс индукции и самоиндукции, связанная с изменением потоков и , идет на приращение магнитной энергии системы и на механическую работу:
.
из данной формулы можно получить частные случаи:
а)
если потоки постоянны (
= const), то
;
б)
если токи постоянны (
= const), то
.
В
обоих случаях можно записать
.
Полученные частные формулы пригодны для системы, состоящей из любого числа контуров.
6. Ток смещения эквивалентен току проводимости в отношении способности создавать магнитное поле. Токи смещения существуют лишь там, где меняется со временем электрическое поле. В диэлектриках ток смещения складывается из тока смещения в вакууме и тока поляризации – величины, обусловленной движением связанных зарядов.
7. Уравнения Максвелла в сжатой форме выражают совокупность наших сведений об электромагнитном поле.
В уравнении (54 а) под понимается как вихревое электрическое поле, так и электростатическое.
Если поле стационарное ( = const, = const), уравнения Максвелла распадаются на две группы независимых уравнений:
,
;
,
.
Для нахождения полей и удобно пользоваться уравнениями Максвелла в дифференциальной форме:
,
;
,
.
Но
эти уравнения предполагают, что все
величины в пространстве и времени
изменяются непрерывно. В случае наличия
поверхностей разрыва эти уравнения
дополняются граничными условиями,
которые должны удовлетворять
электромагнитное поле на границе раздела
двух сред:
.
Уравнения
Максвелла также дополняются материальными
уравнениями. Они наиболее просты в
случае достаточно слабых электромагнитных
полей, медленно меняющихся в пространстве
и во времени:
,
где
–
электрическая и магнитная постоянные;
–
диэлектрическая, магнитная проницаемости
среды и электропроводимость соответственно;
–
напряженность поля сторонних сил.
Примеры решения задач
Пример
1.
Две катушки намотаны на общий сердечник.
Индуктивность первой катушки
=
0,16 Гн, второй –
=
1 Гн, сопротивление второй катушки
=
400 Ом. Определить силу тока
во
второй катушке, если ток
=
0,4 А, текущий в первой катушке, выключить
в течение 0,002с.
Решение
Сила тока во второй катушке определяем по закону Ома
,
(а)
где
–
эдс индукции, возникающая во второй
катушке при изменении силы тока в первой.
По закону электромагнитной индукции
,
(б)
– взаимная индуктивность катушек.
,
(в)
где – магнитная постоянная; – магнитная проницаемость среды; – площадь поперечного сечения сердечника; – его длина; – число витков первой и второй катушек.
(г)
Учитывая (г), формулу (в) запишем в следующем виде:
.
(д)
Из формул (а), (б) и (д) следует:
.
Подставляем
числовые значения и получаем результат
.
Пример
2.
В некоторой плоскости лежат два круговых
витка 1 и 2 , центры которых совпадают.
Радиусы витков
и
.
В витке 1 течет ток
.
Найти магнитный поток
,
охватываемый витком 2, если
.
Решение
Согласно
теореме взаимности
.
Если ток пропускается по контуру 2, магнитный поток , создаваемый этим током через виток 1 при условии , имеет вид:
=>
.
Пример
3.
Вдоль оси симметрии тороидальной
катушки, имеющей прямоугольное сечение,
проходит длинный прямой провод. Внутренний
радиус катушки
,
внешний –
,
высота сердечника
.
Число витков катушки
,
внешняя среда – воздух. Найти амплитудное
значение эдс, индуцируемой в этой
катушке, если по прямому проводу течет
переменный ток
.
Решение
По закону электромагнитной индукции
,
,
где
–
магнитный поток сквозь поперечное
сечение катушки:
Максимальное значение эдс:
.
Пример 4. Сравните энергии, содержащиеся в вакууме в объёме = 1 л, если он пронизан: 1) однородным электрическим полем с напряженностью = 100 кВ/м; 2) однородным магнитным полем с индукцией = 1 Тл.
Решение
Энергия
электрического поля
.
Энергия
магнитного поля
;
,
где
–
электрическая постоянная;
–
магнитная постоянная.
Подставим числовые значения:
=
1 л = 1·10-3
м3;
=
100 кВ/м = 1·105
В/м;
=
1 Тл;
=
8,85·10-12
Ф/м;
=
4
·10-7
Гн/м.
Вычисления
дают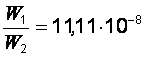 
раз.
Следовательно, практически выгоднее накапливать энергию в магнитном поле.
Пример 5. Катушка без сердечника содержит 1000 витков и имеет длину 50 см. Определить объёмную плотность магнитного поля внутри катушки, если по ней течет ток 2 А.
Решение
Объёмная
плотность энергии магнитного поля
(энергия единицы объёма)
,
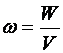где
–
энергия магнитного поля;
–
объём катушки;
,
где
–
индуктивность катушки,
,
,
тогда
.
Подставим
числовые значения:
=
1000;
=
0,5 м;
=
2 А,
Гн/м.
.
Пример
6.
Сравнить величину амплитудных значений
токов проводимости и смещения в среде
с проводимостью
и
относительной диэлектрической
проницаемостью
для
частоты поля
.
Решение
Плотность тока проводимости определяем по закону Ома
,
где
,
так как ток смещения в среде обусловлен
переменным электрическим полем.
.
Плотность тока смещения:
.
Отношение амплитудных значений:
.
Задачи для самостоятельной работы
1.
Через катушку, индуктивность которой
равна 0,021Гн, течет ток, изменяющийся со
временем по закону
,
где
=
5 А,
=
,
=
0,02 с. Найти зависимость от времени
энергии магнитного поля катушки.
Определить величину энергии магнитного
поля в момент времени
.
(Ответ:
).
2.
Две катушки имеют взаимную индуктивность,
равную 0,005 Гн.
В первой катушке сила
тока изменяется по закону
,
где
=
= 10 А,
=
,
=
0,02 с. Найти: 1) зависимость от времени
эдс, индуцируемой во второй катушке; 2)
наибольшее значение этой эдс.
(Ответ:
).
3.
Две катушки расположены на небольшом
расстоянии одна от другой. Когда сила
тока в первой катушке изменяется с
быстротой
,
во второй катушке возникает эдс индукции
=
0,1 В. Определить коэффициент взаимной
индукции катушек.
(Ответ:
20
мГн).
4.
Обмотка тороида с немагнитным сердечником
имеет
=
251 виток. Средний диаметр тороида равен
8 см, диаметр витков равен 2 см. На тороид
намотана вторичная обмотка, имеющая
=
100 витков. При замыкании первичной
обмотки в ней в течение 1 мс устанавливается
сила тока 3 А. Найти среднюю эдс индукции,
возникающей во вторичной обмотке.
(Ответ:
118
мВ).
5.
Две
длинные катушки намотаны на общий
сердечник, их индуктивности соответственно
равны
6,25
Гн и
=
1,25 Гн. Во сколько раз число витков первой
катушки отличается от числа витков
второй катушки.
(Ответ: n = 2,2).
6. Какова взаимная индуктивность двух катушек, индуктивности которых 0,36 Гн и 0,49 Гн, намотанных на общий сердечник.
(Ответ: 0,42 Гн).
7.
Автотрансформатор, понижающий напряжение
с
=
5,5 кВ до 
=
100 В, содержит в первичной обмотке
=
1000 витков. Пренебрегая сопротивлением
первичной обмотки, определите число
витков во вторичной обмотке трансформатора,
если сопротивление вторичной обмотки
=
1,5 Ом, а сопротивление внешней цепи
=
9 Ом.
(Ответ: = 140).
8. В обмотке электромагнита, находящейся под постоянным напряжением, за время 5 мс выделилось количество теплоты, равное энергии магнитного поля в сердечнике. Определите индуктивность обмотки, если её сопротивление = 10 Ом.
(Ответ: 0,1 Гн).
9.
Соленоид без сердечника длиной 0,5 м
содержит 1500 витков. Объёмная плотность
энергии магнитного поля внутри соленоида
равна
.
Чему равна сила тока в соленоиде?
(Ответ: = 0,21 А).
10. По обмотке соленоида, в который вставлен железный сердечник, течет ток 1,2 А. Соленоид имеет длину 0,6 м, площадь поперечного сечения 15 см2 и число витков 400. Определить энергию магнитного поля соленоида.
(Ответ: = 0,432 Дж).
11.
При разрядке цилиндрического конденсатора
длиной 10 см и внешним радиусом 1 см
плотность тока смещения
.
Какой ток течет в подводящих проводах?
(Ответ:
=
).
12. Длинный цилиндрический конденсатор заряжен от источника эдс. Пренебрегая краевыми эффектами, докажите, что ток смещения в диэлектрике, заполняющем пространство между обкладками конденсатора, равен току в цепи источника эдс.
13.
Найти индуктивность единицы длины
кабеля, представляющего собой два
тонкостенных коаксиальных цилиндра,
если радиус внешнего цилиндра в
раз
больше, чем радиус внутреннего. Магнитную
проницаемость среды между цилиндрами
считать равной единице.
(Ответ:
).
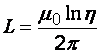14. Определить индуктивность тороидального соленоида из витков, внутренний радиус которого равен , а поперечное сечение имеет форму квадрата со стороной . Пространство внутри соленоида заполнено однородным парамагнетиком с магнитной проницаемостью .
(Ответ:
).
15.
По обмотке длинного соленоида со стальным
сердечником течет ток 2,5 А, число витков
на единицу длины соленоида
.
Найти объёмную плотность энергии
магнитного поля в сердечнике соленоида.
(Ответ:
).
16.
Внутри длинного соленоида радиусом 10
см и числом витков на единицу длины
находится
катушка радиусом 2 см и число витков
=
300, причем их оси параллельны.
1) найти взаимную индуктивность катушки и соленоида;
2) что произойдёт, если радиус катушки увеличить в полтора раза?
3) что произойдёт, если в полтора раза увеличить радиус соленоида?
(Ответ: 1) = 0,95 мГн; 2) увеличится в 2,25 раза; 3) не изменится).
17. Чему равна плотность энергии в центре витка радиусом 8 см, по которому течет ток 30 А?
(Ответ:
).
18. Чему равна плотность энергии магнитного поля длинного прямолинейного проводника круглого сечения радиусом 2 мм с током 20 А: 1) вблизи поверхности провода; 2) на расстоянии 1 м от него?
(Ответ:
1)
2)
).
19. На железное кольцо намотано 200 витков провода. Определить энергию магнитного поля, если при токе 2,5 А магнитный поток в железе равен 0,5 мВб.
(Ответ:
0,13
Дж).
20. Напряженность магнитного поля соленоида со стальным сердечником возросла от = 200 А/м до = 800 А/м. Во сколько раз изменилась объёмная плотность энергии магнитного поля?
(Ответ: возросла в 9,3 раза)
21. Пространство между двумя концентрическими металлическими сферами заполнено однородной слабо проводящей средой с удельным сопротивлением и диэлектрической проницаемостью . В момент времени 0 внутренней сфере сообщили некоторый заряд. Найти: а) связь между векторами плотностей тока смещения и тока проводимости в произвольной точке среды в один и тот же момент; б) ток смещения через произвольную замкнутую поверхность, расположенную целиком в середине и охватывающую внутреннюю сферу, если заряд этой сферы в данный момент времени равен .
(Ответ:
)
22.
Показать, что из уравнений Максвелла
следует закон сохранения электрического
заряда, т. е.
.
23. В работах П.Л. Капицы получены магнитные поля Н = 3∙107 А/м. Вычислить торцевые сжимающие напряжения, действующие на соленоид. Изобразить схематически направления действия этих сил.
(Ответ:
).
24.
В эксперименте по измерению тока смещения
использовался конденсатор ёмкостью
=
100 пФ с воздушным промежутком между
пластинками в форме дисков радиусом
=
40 см. На конденсатор подавалось напряжение
по синусоидальному закону
;
кВ,
=
50 с-1.
Какой была максимальная величина тока
смещения между пластинками конденсатора
в этом эксперименте?
(Ответ: = 6,5 мА).
25.Тонкое кольцо радиусом 20 см, несущее равномерно распределенный заряд 45 мкКл, движется с постоянной скоростью 15 м/с. Плоскость кольца все время остаётся ортогональной направлению движения. В какой точке на оси кольца плотность тока смещения равна нулю?
(Ответ: на расстоянии 14 см от оси)
26. Тонкое кольцо радиусом 20 см, несущее равномерно распределенный заряд 45 мкКл, движется с постоянной скоростью. Плоскость кольца все время остаётся перпендикулярной направлению движения. На расстоянии 14 см от оси кольца плотность тока смещения равна нулю. С какой скоростью движется кольцо?
(Ответ:
15
м/с).
27. Вычислить взаимную индуктивность длинного прямого провода и прямоугольной рамки со сторонами и . Рамка и прямой провод лежат в одной плоскости, причем ближайшая к проводу сторона рамки длины параллельна проводу и отстоит от него на расстоянии .
(Ответ:
).
28. Ток течет по длинному прямому проводнику круглого сечения с магнитной проницаемостью . Найти энергию магнитного поля внутри провода в расчете на единицу длины.
(Ответ:
).
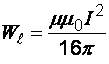29. Железный сердечник, имеющий форму тора с круглым сечением радиуса = 3,0 см, несет на себе обмотку из = 1000 витков, по которой течет ток = 1,0 А. Средний радиус тора = 32 см. Оценить магнитную энергию в сердечнике.
(Ответ:
,
где
).
30.
Тонкое кольцо из магнетика с площадью
поперечного сечения
имеет
средний диаметр
30
см и несёт на себе обмотку из
=
800 витков. В кольце сделана поперечная
прорезь ширины
=
2,0 мм. При некотором токе в обмотке
магнитная проницаемость магнетика
=
1400. Пренебрегая рассеянием поля на краях
зазора, найти:
а) отношение магнитной энергии в зазоре и магнетике;
б) индуктивность системы.
(Ответ: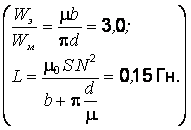
).