2.1. Сила Лоренца. Движение заряженной частицы в однородном постоянном магнитном поле

Основные формулы

     Сила, действующая на электрический заряд , движущийся со скоростью  в магнитном поле

 

,                                             (18)

где  – вектор магнитной индукции поля.

     Модуль силы, действующей на заряженную частицу, движущуюся в магнитном поле

,                                            (19)

где  – модуль заряда частицы;  – модуль вектора скорости;  – модуль вектора индукции магнитного поля,  –  угол между векторами  и .

     Направление силы  определяется по правилу левой руки:

если ладонь левой руки расположить так, чтобы в нее входил вектор магнитной индукции , а четыре вытянутых пальца направить вдоль скорости движения положительного заряда (против направления движения отрицательного заряда), то отогнутый на 90° большой палец покажет направление силы, действующей на заряд.

     Если заряд движется в области, где существуют одновременно электрическое и магнитное поля, то на него действует полная сила

,                                      (20)

формула (20) называется формулой Лоренца.

Методические рекомендации

1. Полная электромагнитная сила (сила Лоренца), действующая на заряд, определяется формулой (20). Данная формула справедлива как для постоянных, так и для переменных электрических и магнитных полей.

Эту силу разделяют на электрическую и магнитную составляющие. Если заряженная частица находится только в магнитном поле, то силу,  определяемую выражением (18), обычно и называют силой Лоренца.

Важная особенность силы Лоренца – она всегда перпендикулярна вектору скорости заряда и поэтому не совершает над зарядом работы. Следовательно, в постоянном магнитном поле энергия движущейся заряженной частицы всегда постоянна.

Разделение полной электромагнитной силы на электрическую и магнитную зависит от выбора системы отсчета, так как магнитная составляющая силы Лоренца меняется при переходе от одной системы отсчета к другой, а значит, меняется и электрическая составляющая.

2. Под действием силы Лоренца заряженные частицы движутся в магнитном поле по криволинейным траекториям. Характер движения частицы в магнитном поле зависит от угла между первоначальным направлением скорости движения частицы и направлением линий индукции магнитного поля.

     Если скорость частицы перпендикулярна линиям магнитной индуции, то частица движется по круговой траектории (рис. 23).

Радиус окружности траектории

;

 

 

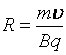Рис. 23

 

период вращения частицы по окружности:

,

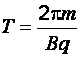где  – масса частицы;  – модуль скорости частицы;  – модуль вектора индукции магнитного поля;  – модуль электрического заряда.

     Если заряженная частица движется вдоль линий магнитной индукции, сила Лоренца на нее не действует и характер ее движения не меняется.

     Если угол  между первоначальным направлением скорости частицы и линиями магнитной индукции не равен ни 0°, ни 90°, ни 180°, траектория движения частицы представляет собой винтовую линию, накручивающуюся на линии магнитной индукции (рис. 24).

 

 

Рис. 24

 

 – тангенциальная составляющая скорости ; ;

 – нормальная составляющая скорости; ;

 – шаг винтовой линии; .

3. При движении заряженной частицы в области пространства, занятой одновременно и электрическим и магнитным полями характер ее движения зависит от направления этих полей и величины сил, действующих с их стороны, а также от скорости частицы.

► Векторы  и  взаимно-перпендикулярны и скорость  положительно заряженной частицы перпендикулярна силовым линиям этих полей. В этом случае на частицу действуют две силы: электрическая  и магнитная , которые могут быть как сонаправлены, так и противоположно направлены. Если силы противоположно направлены и равны по модулю ( ), то частица будет двигаться равномерно и прямолинейно, согласно первому закону Ньютона.

В случае  если силы не уравновешивают друг друга, то движение частицы будет сложным: она будет двигаться с ускорением вдоль линии напряженности электрического поля и совершать вращательное движение вокруг линии индукции магнитного поля.

Если силы, действующие на движущуюся заряженную частицу сонаправлены, то движение частицы также будет представлять суперпозицию двух движений: прямолинейного с ускорением вдоль линий вектора  и вращательного вокруг линий вектора .

► Частица влетает в область пространства параллельно векторам  и . В этом случае на нее действует только электрическая сила  (сила Лоренца , так как  и ). Под действием этой силы  частица движется прямолинейно с ускорением .

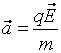Примеры решения задач

Пример 1. Протон влетает в однородное магнитное поле с индукцией 20 мкТл перпендикулярно линиям индукции магнитного поля. Сколько оборотов в секунду будет делать протон в магнитном поле?

Решение

На заряженную частицу в магнитном поле действует сила

,                                                 (а)

где  – заряд частицы,  – индукция магнитного поля,  – скорость частицы,  – угол между векторами  и .

В данной задаче , значит протон будет двигаться в магнитном поле по окружности радиуса  с центростремительным (нормальным) ускорением

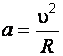                                                   (б)

По второму закону Ньютона

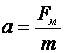,                                                   (в)

где  – масса частицы.

Приравнивая правые части выражений (б) и (в), с учетом формулы (а), получаем

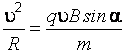,                                           (г)

так как , то после небольшого преобразования получаем

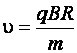.                                                  (д)

С другой стороны,

,                                                    (е)

где  – угловая скорость.

Получаем

.                                                  (ж)

Приравняем правые части уравнений (д) и (л), получим

,

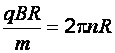откуда выразим  – частоту вращения, т. е. число оборотов в секунду,

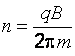.                                                    (и)

Размерность: .

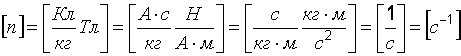Подставляем числовые значения в формулу (и):

.

Вычисления дают .

 

Пример 2. Электрон, имеющий скорость 8·10⁶ м/с, влетает в однородное магнитное поле с индукцией 31,4 мТл под углом 30° к его направлению. Определите радиус и шаг винтовой линии, по которой будет двигаться электрон (рис. 24).

Решение

Скорость  разложим на две составляющие: тангенциальную , параллельную линиям индукции магнитного поля и нормальную ,  перпендикулярную им,

;                                                 (а)

.                                                 (б)

На электрон действует магнитная сила (благодаря нормальной составляющей скорости)

.                                                  (в)

Под действием этой силы электрон будет двигаться по окружности радиуса , который можно найти из условия:

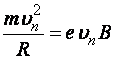,                                                 (г)

так как сила Лоренца является центростремительной силой.

Из формулы (г) получаем

,                                                      (д)

где  – модуль заряда электрона;  – масса электрона;  – индукция магнитного поля.

Вдоль силовых линий поля магнитная сила не действует, поэтому частица движется прямолинейно с постоянной скоростью .

В результате суперпозиции двух движений электрон будет двигаться по винтовой линии радиусом  и шагом винта :

,                                                 (е)

где  – период движения по окружности,

.                                                 (ж)

С учетом формул (б), (д) и (ж), уравнение (е) принимает вид:

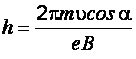.                                            (и)

Размерность: .

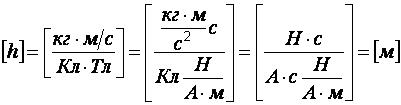Подставляем числовые данные в выражение (и):

.

Вычисления дают:

.

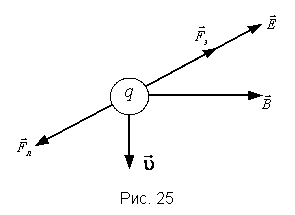
Пример 3. Перпендикулярно магнитному полю с индукцией 0,1 Тл возбуждено электрическое поле напряженностью 1·105 В/м. Перпендикулярно обоим полям, не отклоняясь от прямолинейной траектории, движется заряженная частица. Найти скорость этой частицы (рис. 25). Решение Согласно условию задачи, частица движется равномерно и прямолинейно ( ). По первому закону Ньютона геометрическая сумма сил, действующих на частицу, равна нулю. В данном случае на частицу действует сила Лоренца , где  – электрическая составляющая силы Лоренца,  – её магнитная составляющая (рис. 25).

Следовательно, , т. е. электрическая и магнитная силы равны по модулю и противоположно направлены:

откуда скорость частицы равна:

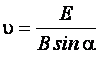
Согласно условию    ( ), поэтому

.

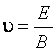Размерность:

 

.

Подставляем числовые данные: .

Получаем при вычислении: .

 

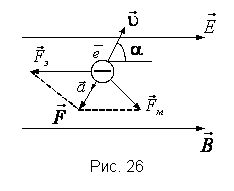
Пример 4. Электрон влетает со скоростью 600 м/с в область пространства, где имеются сонаправленные однородные электрическое и магнитное поля, под углом 60° к силовым линиям полей. Напряженность электрического поля 0,2 кВ/м, индукция магнитного поля 20 мТл. С каким ускорением станет двигаться электрон в этой области пространства? (рис. 26). Решение Согласно второму закону Ньютона, ускорение электрона имеет вид: , где  – сила Лоренца, действующая на электрон со стороны электрического и магнитного полей;  – масса электрона. Сила Лоренца определяется по формуле

,

где  – электрическая составляющая силы Лоренца;  – её магнитная составляющая (рис. 26).

Вектор направлен противоположно вектору , так как заряд электрона отрицательный. Вектор магнитной силы  перпендикулярен вектору магнитной индукции. Следовательно, векторы  и  взаимно-перпендикулярны.

Модуль силы находится по теореме Пифагора:

,

где    – модуль заряда электрона (элементарный заряд).

Ускорение

.

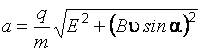Направление  совпадает с направлением вектора , определяемом по правилу сложения векторов.

Подставим числовые значения:

 = 600 м/с;  = 60°; = 0,2 кВ/м = 200 В/м;  = 20 мТл = 2·10^-2 Тл;       = 1,6 ·10^-19 Кл;  = 9,11·10^-31 кг.

Вычисления дают:  = 3,5 ·10¹³ м/с².

 

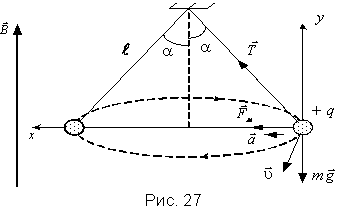
Пример 5. Шарик массой , заряженный положительным зарядом  и подвешенный на нити длиной , движется по окружности в вертикальном однородном магнитном поле с индукцией. Определите кинетическую энергию шарика, если во время движения нить образует угол  с вертикалью.

Решение

Выберем систему отсчета x0y, начало которой поместим в ту точку пространства, где находится шарик в начальный момент времени. Предположим, что нить – невесома, нерастяжима и неэлектропроводна. Заряженный шарик примем за материальную точку. Заряд шарика будем считать точечным.

На шарик действуют сила тяжести , сила натяжения нити и сила  со стороны магнитного поля (рис. 27).

По второму закону Ньютона

.                                        (а)

Направление всех сил указано на рис. 27 в предположении, что вектор магнитной индукции направлен вверх, а шарик движется по часовой стрелке.

Запишем уравнение (а) в проекциях на выбранные оси координат

;                                         (б)

.                                           (в)

После преобразования, получаем

      ;                                          (г)

  .                                            (д)

Разделим (г) на (д), получим

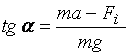.                                            (и)

Шарик движется с нормальным ускорением 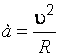,                          (к)

где  – линейная скорость шарика по окружности, – радиус окружности.

Из чертежа следует:

.                                              (л)

Сила Лоренца определяется выражением

,                                           (м)

где  = 90° (по условию задачи),

С учетом выражений (к)–(м) уравнение (и) принимает вид:

,

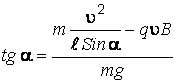или

.

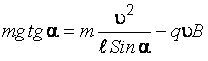Решаем квадратное уравнение относительно переменной :

,

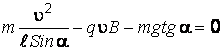получаем

.

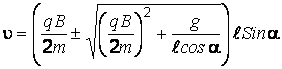Так как модуль скорости  > 0, то из последнего выражения следует:

.

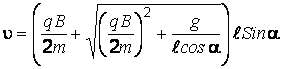Кинетическая энергия определяется соотношением:

.

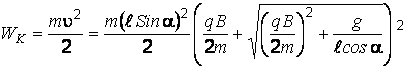Задачи для самостоятельного решения

1. Пучок электронов движется в вакууме в магнитном поле с напряженностью 5,56·10³  А/м по окружности радиусом  3 см. Определите скорость и энергию электронов, период обращения и момент импульса.

(Ответ:  = 36,3·10⁶ м/с; = 33·10^-23 Дж;  = 5·10^-9 с;  = 99·10^-26 (кг·м²)/с).

2.   В однородном магнитном поле с индукцией 0,1 Тл по окружности движется электрон. Найти величину эквивалентного кругового тока, созданного движением электрона.                                                 

(Ответ: = 4,5·10^-10 А).

3.   Однозарядный ион натрия прошел ускоряющую разность потенциалов 1 кВ и влетел в однородное магнитное поле с индукцией 0,5 Тл перпендикулярно силовым линиям поля. Определите относительную массу иона, если он описал окружность радиусом 4,37 см.

(Ответ: 23 а.е.м.).

4. Протон, прошедший ускоряющую разность потенциалов 600 В, влетел в однородное магнитное поле с напряженностью  2,4·10⁴ А/м перпендикулярно линиям магнитной индукции. Найти радиус описанной протоном окружности, его импульс и частоту вращения протона в магнитном поле.

(Ответ: = 0,33 м; = 18·10^-21 Н·с; = 3·10³с^-1).

5. Два иона, имеющие одинаковый заряд и прошедшие одинаковую ускоряющую разность потенциалов, влетели в однородное магнитное поле. Первый ион движется по дуге окружности радиусом 5 см, второй – по дуге окружности радиусом 2,5 см. Определите отношение масс ионов.

(Ответ: ).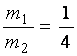

6.   Электрон влетает в область магнитного поля ширины . Скорость электрона перпендикулярна как индукции поля, так и границам области. Под каким углом к границам области электрон вылетит из магнитного поля?                  

(Ответ: , если ;  рад, если ).

7.   Предполагая, что электрон в атоме водорода движется по круговой орбите радиусом 53 пм, определите период обращения электрона вокруг ядра и индукцию магнитного поля, создаваемого движущимся электроном в центре его орбиты.                                            

(Ответ: = 1,5·10^-16 с; = 12,45 Тл).

8.   Частица, имеющая элементарный заряд, влетает в однородное магнитное поле под углом 45° к линиям индукции и движется по винтовой линии с шагом 2 см. Определите импульс частицы, если индукция поля равна 10^-2 Тл.                                                                             

(Ответ: = 7,2·10^-24 кг·м/с).

9.   Электрон, кинетическая энергия которого 1,5 МэВ, движется по окружности в однородном магнитном поле с индукцией 20 мТл. Определите период обращения электрона.                                                          

(Ответ:  = 7 нс).

10.  Электрон в однородном магнитном поле движется по винтовой линии радиусом 5 см и шагом 20 см. Определить скорость электрона, если индукция магнитного поля 0,1 Тл.                                            

(Ответ: = 1,04 Мм/с).

11.  Протон, находящийся в магнитном поле с индукцией 20 мТл описывает окружность радиусом 40 см. Найти импульс протона и его кинетическую энергию.                                         

(Ответ: = 1,3·10^-21 кг·м/с;  = 5·10^-16 Дж).

12.  Протон и альфа-частица влетают в однородное магнитное поле перпендикулярно его силовым линиям. Во сколько раз различаются радиусы окружностей, по которым движутся эти частицы, если у них одинаковы: а) скорость; б) кинетическая энергия? Заряд альфа-частицы в два раза больше заряда протона, а масса альфа-частицы в четыре раза больше массы протона.                                                

(Ответ: (а) 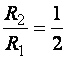; б) ).

13.  В масс-спектрографе заряженная частица, пролетев без начальной скорости ускоряющую разность потенциалов , влетает в однородное магнитное поле индукцией перпендикулярно магнитным линиям. Удельный заряд частицы . Определить диаметр окружности , по которой стала двигаться частица.

(Ответ: ).

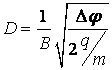14.  В вертикальном направлении создано однородное магнитное поле индукцией . Шарик массой  и зарядом , подвешенный на нити длиной , движется по окружности так, что нить составляет угол  с вертикалью. Найти угловую скорость движения шарика.

(Ответ: ).

15.  Однозарядные ионы гелия и водорода, ускоренные из состояния покоя в электрическом поле напряжением 2 кВ, влетают вместе в магнитное поле индукцией 100 мТл перпендикулярно магнитным линиям. Описав полуокружность, они попадают на фотопластинку. Найти расстояние  между следами этих ионов на фотопластинке.

(Ответ:  = 1,3 см).

16.  Электрон с кинетической энергией 1 кэВ попал в однородное магнитное поле с индукцией  21 мТл и стал двигаться по окружности. Определить магнитный момент эквивалентного кругового тока.

(Ответ: = 7,6·10^-15 А·м²).

17.  Электрон, ускоренный разностью потенциалов 300 В, движется параллельно прямолинейному длинному проводу на расстоянии 4 мм от него. Какая сила действует на электрон, если по проводнику пропустить ток силой 5 А?                                                                                    

(Ответ:  = 4·10^-16 Н).

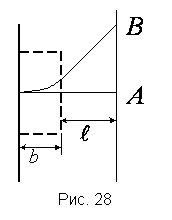
18.  Электрон влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Скорость электрона 4·107 м/с. Индукция магнитного поля 1 мТл. Найти тангенциальное и нормальное ускорения электрона в магнитном поле.     (Ответ:  = 0;  = 7·1015 м/с2). 19.  Пучок электронов, ускоренных разностью потенциалов 300 В, влетает в однородное магнитное поле, направленное от чертежа «к нам» (рис. 28). Ширина поля  = 2,5 см. В отсутствие магнитного поля пучок электронов дает пятно в точке  А флуоресцирующего экрана, расположенного на расстоянии  = 5 см от края полюсов магнита. При включении магнитного поля пятно смещается в точку В. Найти смещение x = АВ пучка электронов, если известно, что индукция магнитного поля 14,6 мкТл.

(Ответ: x = 4,9 см).

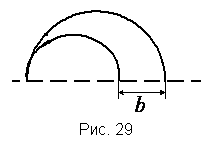
20.  S   В установке для разделения изотопов U235 и U238 пучок однократно ионизованных ускоренных ионов с энергией 5 кэВ попадает от источника через щель S (рис. 29) в однородное магнитное поле, перпендикулярное к плоскости рисунка. В магнитном поле ионы разных масс движутся по различным окружностям и, совершив полуоборот, попадают в приемники. Конструкция последних должна быть такова, чтобы расстояние между пучками изотопов на выходе было не меньше  = 5 мм. Каково должно быть магнитное поле, удовлетворяющее этому условию?                 (Ответ:  4000 Гс).

21.  В конденсаторе, электроды которого составляют часть коаксиальных цилиндрических поверхностей радиусами 5 и 6 см, вдоль оси цилиндров действует однородное магнитное поле с индукцией 0,2 Тл (рис. 30). Через узкую щель в диафрагме АА в конденсатор влетает α-частица с энергией 1 кэВ. Какую разность потенциалов следует создать между электродами конденсатора, чтобы α-частица прошла посередине между электродами? (Внешний электрод имеет отрицательный потенциал).

(Ответ:  = 38,5 В).

22.  В магнетроне анод представляет металлический цилиндр радиусом =1 см, а катод – металлическую нить радиусом , расположенную по оси цилиндра (рис. 31). Постепенно увеличивая индукцию магнитного поля, направленного вдоль оси цилиндра, добились того, что при анодном напряжении 100 В и индукции 6,7·10^-3 Тл анодный ток стал равен нулю. Какое значение удельного заряда получается по результатам этого опыта?

(Ответ:  = 1,76·10¹¹ Кл/кг).

                                   

 

                                                                                                    Рис. 30                                                                                   Рис. 31

 

23.  Магнитное поле напряженностью 8 кА/м и электрическое поле напряженностью 1 кВ/м направлены одинаково. Электрон влетает в электромагнитное поле со скоростью 10⁵ м/с. Найти нормальное, тангенциальное и полное ускорение электрона. Задачу решить для случая, когда скорость электрона направлена параллельно силовым линиям полей.

(Ответ:  = 0;  = 1,76·10¹⁴ м/с²).

24.  Магнитное поле напряженностью 8 кА/м и электрическое поле напряженностью 1 кВ/м направлены одинаково. Электрон влетает в электромагнитное поле со скоростью 10⁵ м/с. Найти нормальное, тангенциальное и полное ускорение электрона. Задачу решить для случая, когда скорость электрона направлена перпендикулярно силовым линиям полей.

 (Ответ: = 0; 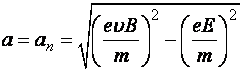 = 2,5·10¹⁴ м/с²).

25.  Магнитное поле с индукцией 0,5 мТл направлено перпендикулярно электрическому полю напряженностью 1 кВ/м. Электрон влетает в электромагнитное поле перпендикулярно к плоскости, в которой лежат векторы и . Найти скорость электронов, если при одновременном действии обоих полей пучок не испытывает отклонения. Каким будет радиус траектории движения электронов при условии включения одного магнитного поля?                                                                            

(Ответ: = 2·10⁶ м/с;   = 2,3 см)

26.  Электрон влетает в плоский горизонтальный конденсатор параллельно его пластинам со скоростью 10⁷ м/с. Длина конденсатора 5 см. Напряженность электрического поля конденсатора 10 кВ/м. При вылете из конденсатора электрон попадает в магнитное поле, перпендикулярное к электрическому. Индукция магнитного поля 10 мТл. Найти радиус и шаг винтовой траектории электрона в магнитном поле.   

(Ответ:  = 5 мм;  = 3,6 см).

27.  Протон влетел в скрещенные под углом 120° магнитное и электрическое поля. Определить ускорение протона, если его скорость 4·105 м/с перпендикулярна векторам  и , напряженность электрического поля  20 кВ/м, индукция магнитного поля 50 мТл.                        

(Ответ:  = 3,3·10¹² м/с²)

28.  Через сечение  алюминиевой пластинки ( – толщина,  – высота) пропускается ток  = 5 А. Пластинка помещена в магнитное поле, перпендикулярное к ребру  и направлению тока. Найти возникающую при этом поперечную разность потенциалов. Индукция магнитного поля = 0,5 Тл. Толщина пластинки  = 0,1 мм. Концентрацию электронов проводимости считать равной концентрации атомов.

(Ответ:  = 2,7 мкВ).

29.  Через сечение  медной пластинки ( – толщина,  – высота) пропускается ток   = 20 А. При помещении пластинки в магнитное поле, перпендикулярное к ребру  и направлению тока, возникает поперечная разность потенциалов = 3,1 мкВ. Индукция магнитного поля  = 1 Тл. Найти концентрацию электронов проводимости в меди и их скорость при этих условиях.                                                  

(Ответ:  = 8,1 ·10²⁸ м^-3;  = 0,31 мм/с).

30.  Заряженная частица, двигаясь перпендикулярно скрещенным под прямым углом электрическому ( = 400 кВ/м) и магнитному ( = 0,25 Тл) полям, не испытывает отклонений от своей траектории при определенной скорости. Определить эту скорость и возможные отклонения от нее, если значения индукции магнитного и напряженности электрического полей могут быть обеспечены с точностью, не превышающей 0,2 %.

 (Ответ: = 1,6·10⁶ м/с;  = 6,4 ·10³ м/с).
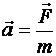