1.5Жорданов базис, существование и единственность.

Матрица, имеющая блочно диагональный вид, по главной диагонали которой расположены жордановы клетки, называется жордановой формой. Базис, в котором матрица линейного преобразования имеет жорданову форму называется жордановым.

Следствие 1.7. Для любого линейного преобразования конечномерного векторного пространства над полем комплексных чисел существует жорданов базис.

Доказательство. Базис, построенный при доказательстве предыдущей теоремы, является жордановым. Следовательно, для построения жорданова базиса достаточно линейное пространство расщепить в прямую сумму корневых подпространств и для каждого корневого подпространства найти жорданов базис.

Теорема 1.6. Жорданова форма матрицы единственна, с точностью до перестановок клеток.

Доказательство. Пусть - корни характеристического многочлена. Построим жорданов базис. Пронумеруем жордановы клетки. Пусть жорданова клетка с номером i (i=1,…,r) имеет собственное число и размер . Жордановой клетке в жордановом базисе соответствует цепочка . Первый вектор в цепочке имеет высоту , каждый следующий – на единицу меньше предыдущего. Обозначим через количество жордановых клеток с собственным числом порядка k. В корневом подпространстве содержатся все векторы высоты не большей j, следовательно, . С другой стороны, вектор x из раскладывается по тем векторам жорданова базиса, которые соответствуют собственному числу и имеют высоту не больше j. Действительно, разложим x по базису. Поскольку пространство разложено в прямую сумму корневых подпространств, то коэффициенты разложения при векторах принадлежащих другим корневым подпространствам равны нулю. Таким образом, . Применим к обеим частям равенства преобразование , получим . В силу линейной независимости векторов жорданова базиса, все коэффициенты в нем равны 0, и, значит, . Тем самым установлено равенство . Из полученных равенств выводим при k>1 и . Поскольку размерность корневых подпространств от выбора базиса не зависит, то теорема доказана.

1.6Построение Жорданова базиса.

Опишем алгоритм построения жорданова базиса.

1. Найдем все собственные числа линейного преобразования.

2. Для каждого собственного числа построим цепочку корневых подпространств . Положим .

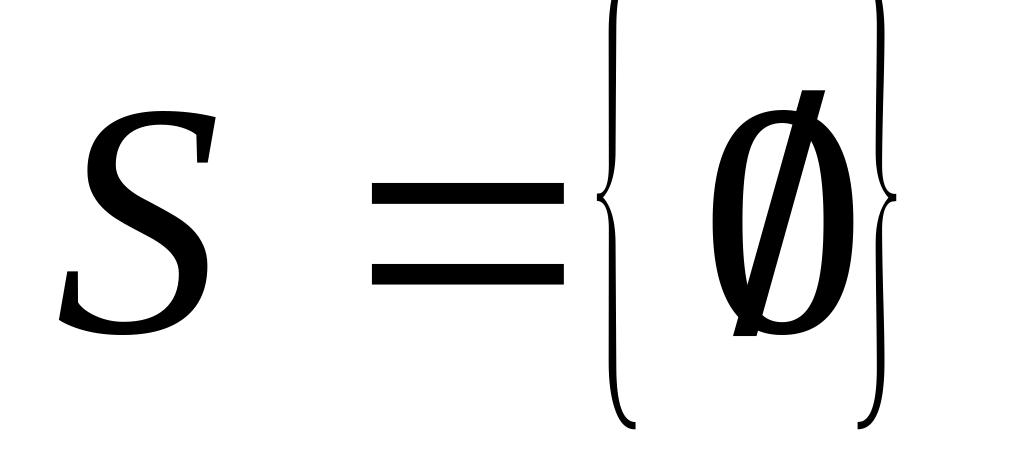3. Положим 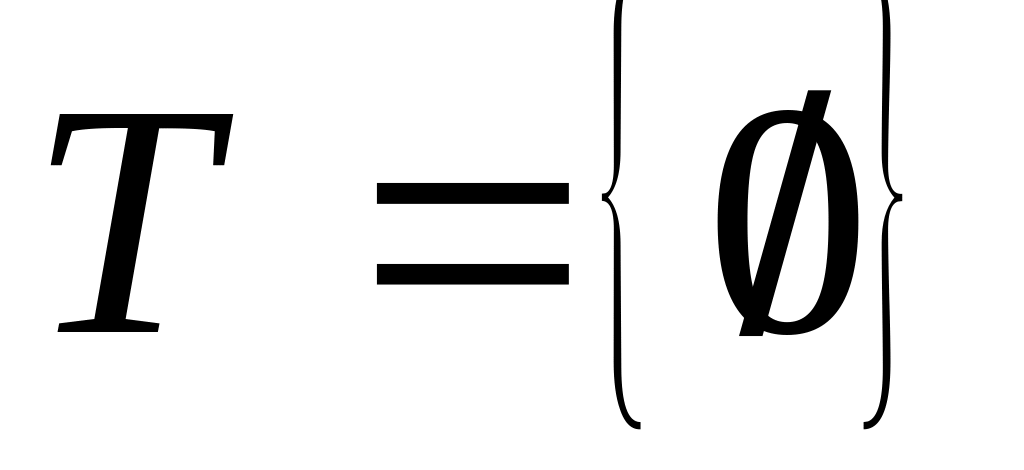i=1. Строим систему векторов T следующим образом:

   1. Добавим к T векторы из S высоты i.

   2. Если система векторов T образует базис 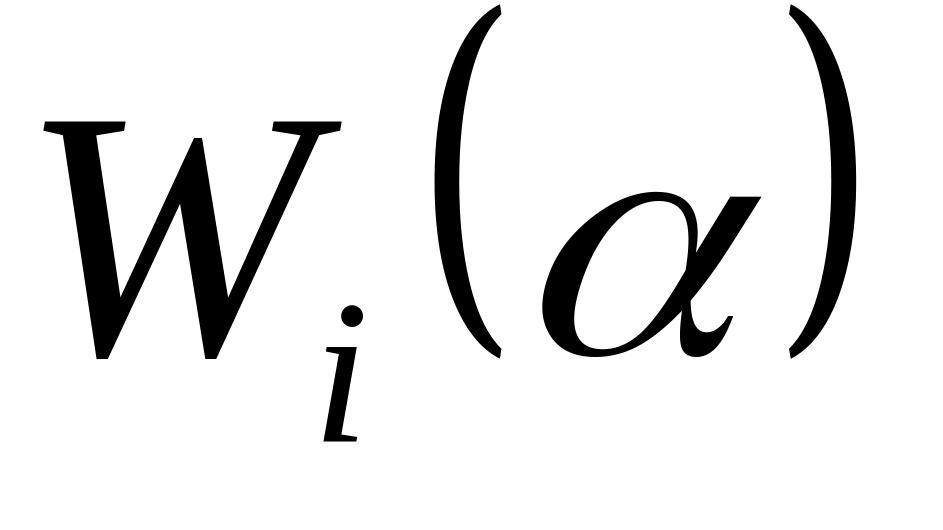, то переходим на шаг 4, а в противном случае на шаг 3.3.

   3. Дополним систему векторов T до базиса и положим i=i+1. Если i>k, то перейдем на шаг 4, а иначе вернемся на шаг 3.1.

4. Среди векторов из T не принадлежащих S выберем вектор e наибольшей высоты (эта высота равна i-1). Добавим к S векторы 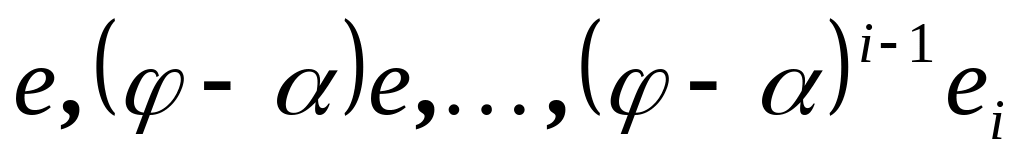. Если система векторов S еще не является базисом , то перейдем на шаг 3.

2 Алгебра, полугруппы, группы

2.1Отношение, операция, алгебра.

Пусть M некоторое множество. Любое подмножество задает k-местное отношение (при k=1 отношение называется унарным, k=2 – бинарным), которое принимает значение «истина», если набор из k-элементов принадлежит и «ложно» - иначе. Каждое k+1-местное отношение задает k-местную операцию (функцию) f следующим образом: набор принадлежит тогда и только тогда, когда . При k=1 операция называется унарной, а при k=2 – бинарной. Бинарные операции часто записывают не в виде f(a,b) а как afb.

Множество M с определенными на нем отношениями и операциями называется алгеброй. Множество отношений и операций называется сигнатурой алгебры . Алгебру записывают как .

Допустим в множестве M нашлось такое подмножество U, что на нем определены все отношения и операции из сигнатуры алгебры. Тогда алгебра называется подалгеброй алгебры .