9 Приведение квадратичных форм

9.1 Приведение квадратичных форм к главным осям.

Рассмотрим квадратичную форму . Матрица A является симметричной. Линейное преобразование, заданное матрицей A, является самосопряженным и для этого преобразования существует ортонормированный базис из собственных векторов. Другими словами, найдется ортогональная матрица T ( ), что , где - собственные числа A. Поскольку , то квадратичная форма ортогональной заменой переходит в форму . Приведение квадратичной формы к каноническому виду ортогональным преобразованием называется приведением к главным осям. Полученный факт оформим в виде теоремы.

Теорема 9.35. Квадратичная форма при помощи ортогонального преобразования всегда может быть приведена к канонической форме , де - собственные числа A.

Отметим, что для квадратичной формы выполняется закон инерции. Следовательно, используя теорему Якоби, можно определить число положительных и число отрицательных собственных значений. Собственные значения матриц A и A-tE отличаются на t, поэтому, определяя число положительных и отрицательных собственных значений матрицы A-tE, мы, тем самым, определим количество собственных значений матрицы A меньших t. Выбирая различные t можно найти собственные числа с любой точностью.

9.2 Приведение пары квадратичных форм

Рассмотрим задачу выбора базиса в котором пара квадратичных форм имеют диагональный вид. Не все пары квадратичных форм можно одновременно привести к диагональному виду, например, формы и xy привести нельзя.

9.2.1Первый способ

Пусть даны квадратичные формы и , причем квадратичная форма - положительно определена. Тогда введем скалярное произведение и найдем ортонормированный базис, а затем приведем первую квадратичную форму к главным осям. Поскольку ортогональное преобразование не меняет скалярное произведение, то обе квадратичные формы будут приведены к каноническому виду.

9.2.2Пучок матриц

Пусть даны квадратичные формы и . Рассмотрим пучок квадратичных форм . Если квадратичные формы и заменой координат x=Py приводятся к каноническому виду, то все формы из пучка приводятся к каноническому виду этой же заменой координат. Пусть и , тогда . Из последнего равенства выводим , то есть многочлен раскладывается на линейные множители над полем вещественных чисел. Из равенства выводим, что i-ый столбец матрицы P удовлетворяет однородной системе уравнений . Таким образом, получается следующий алгоритм приведения пары квадратичных форм к нормальному виду.

1. Раскладываем многочлен на линейные множители. Если разложения не существует, то искомой замены координат не существует.

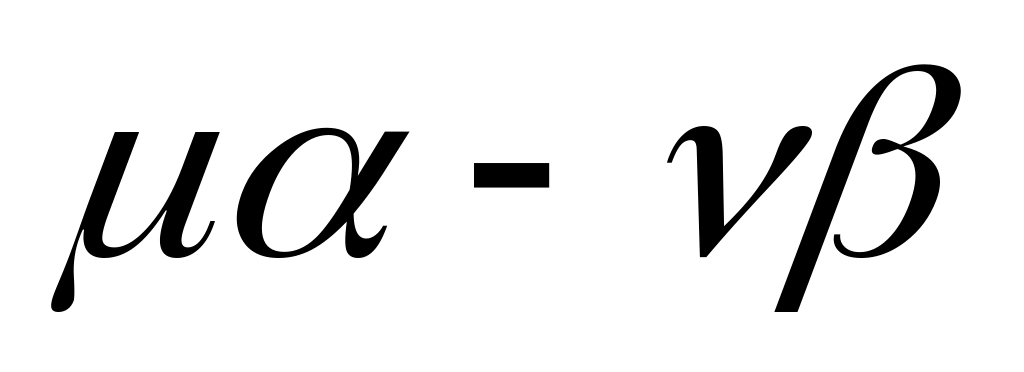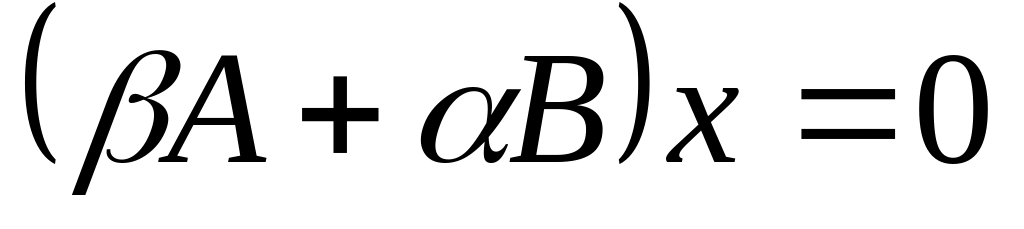2. Для каждого линейного множителя многочлена находим базис подпространства . Если размерность подпространства меньше кратности множителя, то искомой замены координат не существует. В противном случае, будет построен базис, в котором квадратичные формы имеют нормальный вид.

Для обоснования этого подхода требуется показать, что объединение линейно независимых систем векторов, соответствующих разным линейным множителям, образует линейно независимую систему. Доказательство проводится также как и для собственных векторов.