Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский авиационный институт (национальный исследовательский университет)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Алгоритм БИНСлаб работа.doc

Скачиваний:

Добавлен:

27.08.2019

Размер:

1.24 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 33

5.2.5.3 Разработка функционального алгоритма начальной выставки бинс, основанного на использовании метода векторного согласования

Среди различных методов, используемых для начальной выставки БИНС, наибольшего внимания заслуживает метод векторного согласования. К достоинствам этого метода следует отнести, прежде всего, то, что в ряде случаев он позволяет выполнить процесс выставки полностью автономно, т. е. без использования информации от других устройств.

Сущность этого метода состоит в том, что матрица, характеризующая взаимную ориентацию двух трехгранников, всегда может быть вычислена, если в них определены два естественно существующие или искусственно созданные неколлинеарные векторные величины.

Задача начальной выставки бесплатформенной инерциальной навигационной системы заключается в определении начального значения матрицы направляющих косинусов между трехгранником , жестко связанным с объектом и образованным измерительными осями акселерометров и гироскопов БИНС и горизонтным трехгранником .

Алгоритм вычисления это матрицы в процессе начальной выставки можно построить на основе информации о векторе ускорения силы тяжести и либо векторе угловой скорости вращения Земли , либо векторе напряженности ее магнитного поля . Информация об этих векторах априорно известна в базисе , а в трехграннике она может быть получена соответственно с помощью акселерометров и гироскопов БИНС, либо с помощью магнитометров

Процедуру построения этого алгоритма рассмотрим для случая использования двух векторов - вектора силы тяжести и некоторого вектора , в качестве которого в дальнейшем может быть выбран либо вектор угловой скорости вращения Земли , либо вектор напряженности ее магнитного поля .

Полагая, что процесс начальной выставки БИНС осуществляется в тех районах земной поверхности, где эти вектора неколлинеарные, сформируем три взаимно ортогональных орта

(5.2.28)

(5.2.29)

(5.2.30)

В этих соотношениях через и обозначены соответственно модули векторов и .

Учитывая, что и , орт можно записать так

. (5.2.31)

Связь между проекциями этих ортов на оси базисов и , можно описать соотношением

, (5.2.32)

где через обозначены матрицы-столбцы, составленные из проекций ортов соответственно на оси базисов и .

Поскольку векторы и единичные и взаимно ортогональные, из последнего соотношения следует, что матрица может быть вычислена следующим образом:

. (5.2.33)

Равенство (5.2.33) можно записать так

, (5.2.34)

а входящие в него единичные вектора, учитывая формулы (5.2.28) ÷(5.2.30), определить с помощью следующих соотношений

(5.2.35)

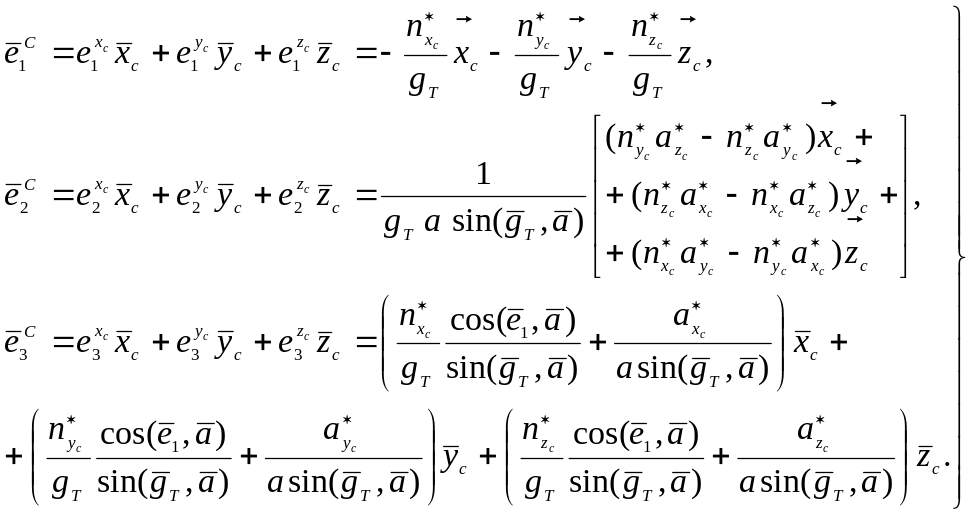(5.2.36)

В этих соотношениях через и обозначены соответственно показания акселерометров и датчиков угловой скорости БИНС либо магнитометров.

Учитывая, что проекции вектора на оси базиса равны

, , , орты , , можно описать следующими соотношениями

(5.2.37)

Если в качестве второго вектора используется вектор угловой скорости вращения Земли, т. е. , то , , , , и равенства (5.2.37) примут вид

(5.2.38)

Подставляя выражения для , , и проекций ортов , , на оси базиса в соотношение (5.2.34), алгоритм вычисления элементов матрицы можно записать так

(5.2.39)

Если же в качестве второго вектора используется вектор напряженности магнитного поля Земли, т. е. , то , , , , и равенства (5.2.37) и (5.2.36) примут вид

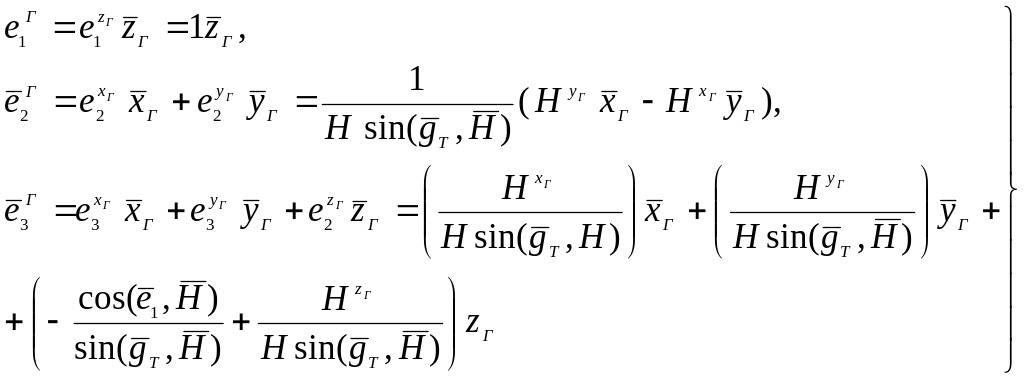(5.2.40)

(5.2.41)

Алгоритм вычисления элементов матрицы в этом случае можно получить, подставив последние выражения для проекций ортов , , и , , соответственно на оси базисов и в формулу (5.2.34).

В случае, когда получение информации о векторе угловой скорости вращения Земли , либо векторе напряженности ее магнитного поля , не представляется возможным, либо определение этой информации осуществляется с неприемлемой точностью, задача начальной выставки БИНС с помощью метода векторного согласования решена быть не может.

В этом случае решение задачи начальной выставки БИНС может быть выполнено на основе сигналов, снимаемых с акселерометров и значении стояночного курса л. а.

Информация о и , получаемая с акселерометров, измерительные оси которых совпадают с продольной осью объекта и осью , направленной по его правому крылу, позволяет определить углы тангажа и крена

, ,

а данные о стояночном курсе объекта, могут быть получены с помощью магнитного либо индукционного датчика курса, измеряющих магнитный курс , и данных о величине магнитного склонения в точке выставки

Матрица , характеризующая положение трехгранника относительно базиса в этом случае может быть вычислена с помощью следующего соотношения

(5.2.42)

Необходимо заметить, что при использовании метода векторного согласования вектора и могут быть определены лишь с погрешностями, обусловленными как ошибками измерительных элементов, используемых при выставке БИНС, так и неточностью задания координат точки старта, а также рядом других факторов. В связи с этим рассмотренные выше алгоритмы позволяют определить не идеальную матрицу , а лишь некоторое ее приближенное значение , характеризующее положение относительно базиса не трехгранника , а некоторого «вычисленного» трехгранника "В" - .

Учитывая изложенное, процесс выставки БИНС обычно осуществляется в два этапа. На первом, по изложенной выше процедуре, находится матрица , а, на втором, определяется ее уточненное значение.

Уточненное значение матрицы можно найти следующим образом.

Представим идеальную матрицу в виде произведения ее значения , полученного на первом этапе выставки, и матрицы малого углового поворота

. (5.2.43)

В этом случае задача нахождения оптимальной оценки матрицы сводится к нахождению матрицы , определяющей положение «вычисленного» трехгранника относительно базиса , рисунок 5.2.1.

Рисунок 5.2.1. Взаимное положение трехгранников , и

Матрицу можно представить в следующем виде

, (5.2.44)

где . (5.2.45)

Поскольку матрица кососимметрическая, то ей в соответствие может быть поставлен вектор малого углового поворота, элементы которого равны недиагональным элементам этой матрицы:

. (5.2.46)

Таким образом, задача определения оптимальной оценки матрицы в данном случае сводится к определению трех элементов вектора .

Этот вектор можно принять за вектор состояния и находить его значение с помощью методов оптимального оценивания.

Для описания поведения этого вектора дифференциальным уравнением вида

, (5.2.47)

где вектор представляет собой гауссову случайную величину с известными математическим ожиданием и корреляционной матрицей , предположим, что трехгранник вращается относительно абсолютного пространства с угловой скоростью . Тогда воспользовавшись модифицированным уравнением Пуассона, поведение матрицы нетрудно описать дифференциальным уравнением

, (5.2.48)

где кососимметрические матрицы

, , (5.2.49)

элементами которых являются проекции абсолютной угловой скорости вращения базисов и , на их оси.

Умножив слева члены в уравнении (5.2.48) на , получим

. (5.2.50)

Левую часть этого равенства, воспользовавшись соотношением , можно представить в виде

. (5.2.51)

Пренебрегая в этом равенстве членами выше первого порядка малости, получим

. (5.2.52)

Теперь, подставив последнее соотношение в уравнение (5.2.50), будем иметь:

. (5.2.53)

Определим теперь входящую в это уравнение вектор матрицу угловых скоростей . Для этого воспользуемся уравнением, описывающим поведение матрицы

, (5.2.54)

характеризующей угловую скорость вращения базиса относительно трехгранника ,

Необходимо заметить, что это вращение обуславливается ошибками вычисления матрицы на первом этапе выставки. Из этого равенства следует, что

. (5.2.55)

Подставив это соотношение в уравнение (5.2.53), получим

. (5.2.56)

В соответствии со свойством подобного преобразования кососимметрических матриц [1], последнее уравнение можно записать так

, (5.2.57)

или, с учетом выражения , представить в виде

, (5.2.58)

где и .

При получении этого уравнения (5.2.57) учтено, что вектор малого углового поворота был поставлен в соответствие матрице , имеющей структуру, определяемую соотношением (5.2.45). Матрицы же , и , описываемые выражениями (5.2.49) и (5.2.54), также кососимметрические, но имеют структуру, отличающуюся от структуры матрицы расположением элементов с отрицательными знаками. Поэтому при получении соотношения (5.2.57) им в соответствие должны быть поставлены вектора , и .

Фигурирующий в уравнении (5.2.58) вектор определяется вектором угловой скорости вращения Земли , а вектор угловой скорости базиса , определяется суммой вектора угловой скорости вращения Земли и вектора абсолютной угловой скорости колебаний объекта относительно Земли в процессе выставки . Поэтому уравнение (5.2.58) можно записать так

. (5.2.59)

Воспользовавшись равенством последнее выражение можно записать и так

, (5.2.60)

. (5.2.61)

Если полагать, что вычисленная на первом этапе выставки матрица постоянна, то в этом случае уравнения (5.2.60) и (5.2.61) примут вид

, (5.2.62)

. (5.2.63)

Соотношения (5.2.61) и (5.2.63), учитывая, что , можно также представить в следующей форме записи

, (5.2.64)

. (5.2.65)

Эти соотношения можно принять в качестве уравнения (5.2.47), описывающего поведение вектора состояния при решении задачи нахождения его оптимальной оценки.

Вектор измерений, необходимый для построения алгоритма фильтра, обеспечивающего нахождения оптимальной оценки малого углового поворота , можно сформировать по информации о векторе ускорения силы тяжести и векторе , в качестве которого, как и раньше, может быть выбран либо вектор угловой скорости вращения Земли , либо вектор напряженности ее магнитного поля .

Поскольку в базисе эти вектора известны априорно, а в базисе , могут быть измерены с помощью акселерометров и гироскопов, входящих в состав БИНС, либо магнитометров, вектор измерений можно сформировать следующим образом:

. (5.2.66)

Опишем связь этих измерений с вектором оцениваемых параметров соотношением

. (5.2.67)

Для этого представим входящие в выражение (5.2.66) вектора и в виде суммы их идеальных значений , а также погрешностей их измерения , и составляющих, вызванных колебаниями объекта относительно Земли в процессе выставки и :

, (5.2.68)

. (5.2.69)

Воспользовавшись соотношением , вектор измерений запишем так

. (5.2.70)

Подставляя в это равенство выражения (5.2.69), (5.2.70) и учитывая, что , а, также пренебрегая слагаемыми и как членами порядка малости выше первого, получим

. (5.2.71)

Учитывая, что и , последнее выражение можно представить в виде

. (5.2.72)

Таким образом, связь вектора с вектором измерений может быть описана соотношением

, (5.2.73)

где , (5.2.74)

. (5.2.75)

Последнее равенство и уравнение (5.2.60)

или (5.2.62)

образуют совокупность соотношений, на основе которых может быть решена задача построения алгоритма нахождения оптимальной оценки вектора .

Представим соотношения (5.2.60) и (5.2.73) в скалярной форме записи

где ,

Из приведенных уравнений видно, что задача нахождения оптимальной оценки вектора малого углового поворота может быть сведена к нахождению оптимальных оценок трех независимых его компонент:

-компоненты , поведение которой описывается уравнением