5. Понятия логического исчисления и выводимости формул. Исчисления высказываний ив.

Логическим исчислением принято называть синтаксическую (т.е. формализованную аксиоматическую) теорию математической логики. Описание всякого исчисления включает:

1. описание алфавита, т.е. множества символов, используемых для построения формул теории;

2. описание языка, т.е. правил построения допустимых последовательностей символов (слов) в алфавите, называемых формулами;

3. задание системы аксиом – некоторого множества истинных формул, называемых аксиомами;

4. определение правил вывода, позволяющих из одних истинных формул получать другие формулы рассматриваемой синтаксической теории.

Исчисление высказываний ИВ – это аксиоматическая логическая система, адекватная алгебре высказываний.

В качестве алфавита исчисления высказываний возьмем следующее множество символов:

1. счетное множество высказывательных переменных, обозначаемых прописными латинскими буквами с индексами и без них;

2. символы логических операций ;

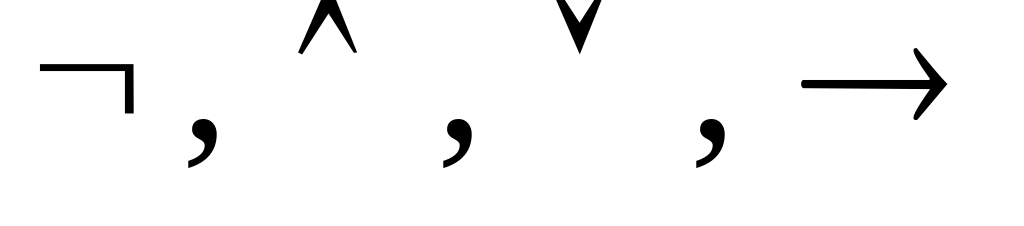3. скобки ( , ).

Формула ( ) называется выводимой из системы формул (1) в алгебре высказываний, что обозначается , . . ,  , тогда и только тогда, когда формула является ТИ-высказыванием, т.е.  .

6. Исчисления предикатов. Автоматическое доказательство теорем методом резолюций.

Предикатное исчесление – это формальная аксиоматическая теория; исчисление, предназначенное для описания логических законов, справедливых для любой непустой области объектов с произвольными заданными на этих объектах предикатами.

Доказательство теорем сводится к доказательству того, что некоторая формула   (гипотеза теоремы) является логическим следствием множества формул   (допущений). Т.е. сама теорема может быть сформулирована следующим образом: "если   истинны, то истинна и  ". Такой метод доказательства теорем называется методом резолюций.

Для доказательства того, что формула G является логическим следствием множества формул   , метод резолюций применяется следующим образом. Сначала составляется множество формул   . Затем каждая из этих формул приводится к КНФ (конъюнкция дизъюнктов) и в полученных формулах зачеркиваются знаки конъюнкции. Получается множество дизъюнктов S. И, наконец, ищется вывод пустого дизъюнкта из S. Если пустой дизъюнкт выводим из S, то формула G является логическим следствием формул  . Если из S нельзя вывести #, то G не является логическим следствием формул  .

7. Формальные определения алгоритма в терминах машины Тьюринга.

Определение. Алгоритм – это процедура, которая позволяет преобразовывать информацию:

• она четко описана

• приводит к результату.

Точные формулировки алгоритмов возникли в тридцатые годы двадцатого века.

Описание любой эффективной процедуры можно найти в терминах машины Тьюринга. Возьмем автомат , образуем , получим, что автомат на ленте работает так: 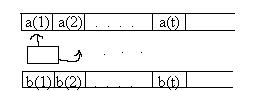. В середине изображена головка, передвигающаяся по ячейкам и содержащая информацию о состоянии в данный момент. Она считывает содержимое ячейки напротив, берет его в качестве очередной входной буквы, а на его место записывает выходную букву. Обобщим несколько ленту, а именно, будем считать, что двигаться можно не только вправо, но и влево, а также можно стоять на месте (а лента бесконечна в обе стороны). После этого получится машина Тьюринга. Команды будем задавать в следующем виде: , что расшифровывается так: в состоянии подается буква , на выходе получается буква , новое состояние – , обозначает направление движения ( – сдвиг влево, – вправо, – отсутствие сдвига). У каждой машины имеется конечный набор команд. Условимся всегда обозначать начальное состояние как , конечное как (когда получается состояние , машина останавливается; если оно никогда не получается, то машина не останавливается и называется неприменимой к ).

Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.