Нормальные формы

Элементарной конъюнкцией называется конъюнкция, в которой участвуют высказывательные переменные или их отрицания.

Элементарной дизъюнкцией называется дизъюнкция, в которой участвуют высказывательные переменные или их отрицания.

Дизьюнктивной нормальной формой называется формула, имеющая вид дизъюнкции элементарных конъюнкций.

Коньюнктивной нормальной формой называется формула, имеющая вид конъюнкции элементарных дизъюнкций.

Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ в каждой конъюнкции которой содержатся точно одно вхождение всех переменных или их отрицаний. Такие конъюнкции называются полными.

Совершенной конъюнктивной нормальной формой (СКНФ) называется КНФ в каждой дизъюнкции которой содержатся точно одно вхождение всех переменных или их отрицаний. Такие дизъюнкции называются полными.

Теорема 4.4. Всякая булева функция (кроме 0) имеет единственную СДН-форму

.

Теорема 4.5. Всякая булева функция (кроме 1) имеет единственную СКН-форму

.

3. Полнота систем логических операций и функций. Алгебра и полином Жегалкина. Теорема Поста.

Система операций  называется полной, если любая логическая операция может быть представлена формулой над .

Так как всякая формула может быть представлена приведенной формулой, то система 0 = {, , } - полна. Полной будет и любая система , через операции которой можно выразить конъюнкцию, дизъюнкцию и отрицание.

Если все операции полной системы * представимы формулами над системой , то  полна, в этом случае говорят, что  сводится к *.

Алгебра над множеством логических функций с двумя операциями  и  называется алгеброй Жегалкина. В алгебре Жегалкина выполняются следующие соотношения:

, , , , а также ассоциативность, коммутативность, идемпотентность конъюнкции и свойства констант.

Теорема 5.1 (Поста). Система булевых функций полна тогда и только тогда, когда она содержит хотя бы одну функцию, не сохраняющую 0, хотя бы одну функцию, не сохраняющую 1, хотя бы одну несамодвойственную функцию, хотя бы одну немонотонную функцию и хотя бы одну нелинейную функцию.

Если в произвольной формуле алгебры Жегалкина, реализующей булеву функцию f, раскрыть скобки и произвести все возможные упрощения, то получится формула, имеющая вид суммы произведений, то есть полинома по mod 2. Такая формула называется полиномом Жегалкина для данной функции. Таким образом, линейной называется функция, полином Жегалкина которой линеен.

4. Предикаты. Операции с предикатами. Формулы алгебры предикатов. Допустимые модели. Приведенные нф.

Предикат можно определить как отображение n-ной степени множества M, называемой местностью или арностью предиката в двухэлементное множество B = {И, Л}

.

Так как предикаты принимают значения из множества B, то для них определены логические операции ~. Кроме того, для предикатов вводятся операции утверждения общности и утверждения существования.

Операция утверждение общности ставит в соответствие высказывательной форме P(x) высказывание (читается как, P(x) истинно для всех x из множества M, на котором определен предикат). Высказывание истинно тогда и только тогда, когда высказывание P(a) истинно для любого элемента .

Операция утверждение существования ставит в соответствие высказывательной форме P(x) высказывание (читается как, существует такой x из множества M, для которого высказывание P(x) истинно). Высказывание истинно тогда и только тогда, когда высказывание P(a) истинно хотя бы для одного элемента .

Определим формулу алгебры предикатов сигнатуры . Так же как и в алгебре высказываний, такое определение является индуктивным.

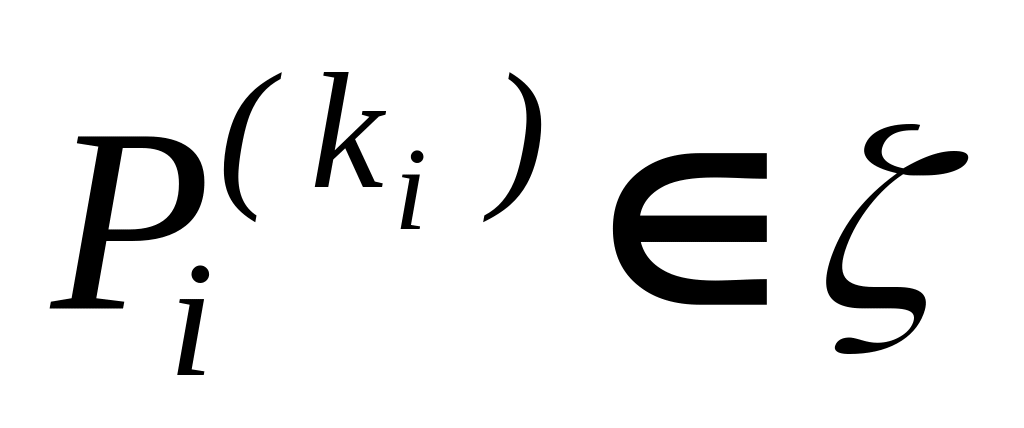1. Если и 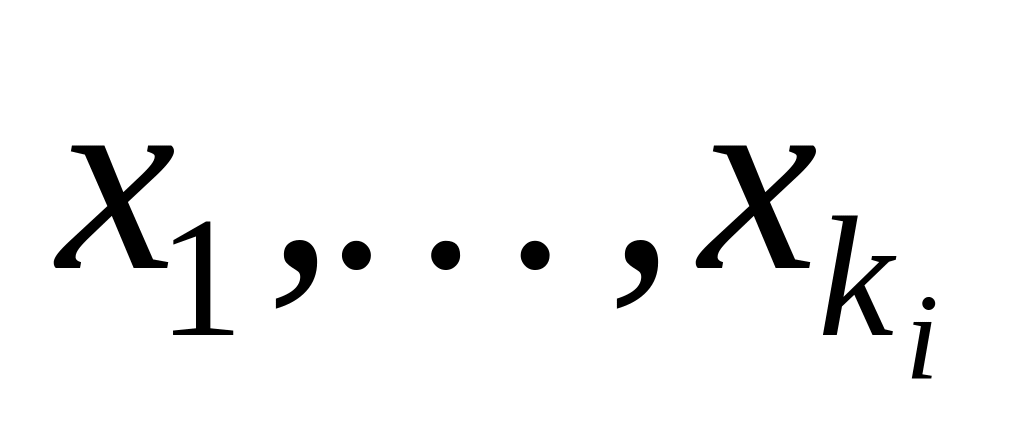– предметные переменные, то выражение 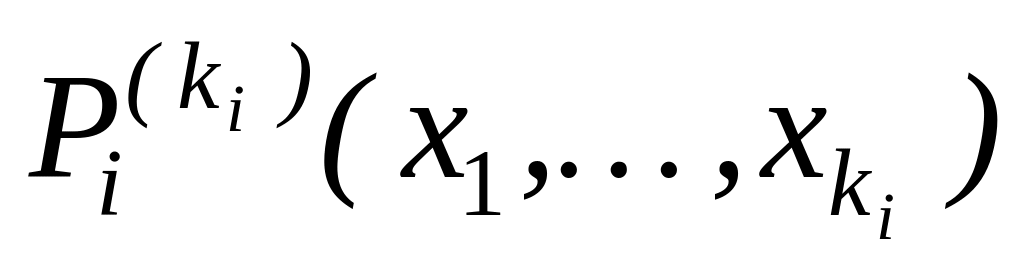есть формула. Такая формула называется атомарной, в ней все вхождения предметных переменных называются свободными.

2. Если U есть формула, в которой имеются свободные вхождения переменной x_i, то выражения x_i (U) и  x_i (U) – формулы, в которых все вхождения x_i являются связанными, а все вхождения остальных предметных переменных такие же, какими они были в формуле U. При этом формула U называется областью действия соответствующего квантора общности или существования.

3. Если U есть формула, то  U – также формула, и все свободные и связанные вхождения предметных переменных в формулу U являются соответственно свободными и связанными вхождениями в формуле  U.

4. Если U и V есть формулы, то выражения (U)  (V), (U)  (V), (U)  (V), (U) ~ (V) также являются формулами, причем все вхождения предметных переменных в этих формулах такие же, как и в формулах U и V.

5. Формулы могут быть образованы только с помощью правил 1 – 4.

Формула логики предикатов, в которой из операций логики высказываний имеются только конъюнкция, дизъюнкция и отрицание, причем отрицание относится только к элементарным предикатам, называется приведенной формой предиката.

Предикатная формула вида   , где  Кi  –  кванторы,  хi  –  различные  связанные  переменные,  а  F – предикатная формула без кванторов, находящаяся в приведенной форме, называется предваренной нормальной формой предиката.