Санкт-Петербургский Государственный
Политехнический Университет
Ф
акультет
Технической Кибернетики
Кафедра Информационных и Управляющих Систем
Лабораторная работа по «тау» №4 Тема: Метод пространства состояний.
Вар: 18.
Выполнил:
Матвеева Наталья
Группа :3084/1
2012
Цель работы:
Анализ системы управления методом пространства состояний.
Задачи работы:
Записать уравнения состояния.
Вычислить собственные числа матрицы состояний и определить устойчивость системы.
Проверить наблюдаемость и управляемость системы.
Вычислить переходную матрицу состояния.
Вычислить отклик системы на заданное входное воздействие, используя:
А)полученную переходную матрицу состояния,
Б)процедуру Фаддеевой построения матрицы передаточных функций,
В)процедуру simulation
Задание:
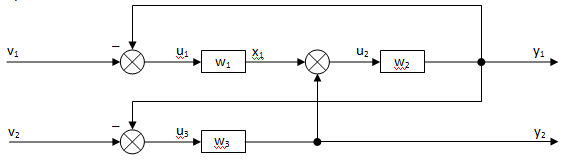
Вид передаточных функций для звеньев(из результатов прошлой лабораторной работы):
(1*)
передаточные функции всей цепи:
;
(2*)
;
Входные воздействия: Начальные условия:
Теоретические основы
Существует 2 подхода к синтезу и анализу САУ. Первый- классический, основанный на преобразованиях Лапласа, Фурье и z-преобразований, представляет собой анализ систем в частотной области. Название же второго метода отождествляют с современной ТАУ. Он базируется на анализе системы во временной области, причем описание системы происходит в пространстве состояний. Что же будет являться состоянием? Состоянием системы в момент времени t=t0 называют минимальный по размеру набор значений переменных, связанных с системой, характеризующих поведение системы в будущем. Здесь следует еще раз подчеркнуть, что будущие значения выходов системы не зависят от характера достижения системой её текущего состояния. Текущие и будущие значения выходов единственным образом определяются состоянием системы и текущим и будущим значением его входов.
Любая система описывается уравнением состояний, имеющим следующий вид:
, где x(t0)-состояние в момент времени t=t0(векторная функция);u(t)-входной сигнал(векторная ф-я) h(),g()-векторные функции от векторных аргументов. Из класса систем, описываемых уравнением состояний выделяют- дифференциальные системы, имеющие след вид:
Именно данный метод описания САУ лег в основу данной лабораторной.
Формирование уравнения состояний
Теоретические основы
А) Запись уравнений состояний линейной стационарной системы с одним входом и одни выходом.
Пусть система задана передаточной
функцией
.
Для выявления состояний системы проводят
её параллельную декомпозицию (разложение
передаточной функции на простые дроби),
затем составляют соответствующую схему
моделирования. Следующим шагом является
непосредственно запись системы, при
этом в качестве переменных состояния
выбирают выходы интеграторов.
В случае если характеристический полином
системы не имеет кратных корней,
параллельная декомпозиция будет иметь
вид:
,а
соответствующая схема моделирования:
Тогда непосредственно система:
(*)
Если же характеристический полином
имеет корни краткости k,
то H(s) после
декомпозиции будет иметь вид
,схема
моделирования
:
При этом в (*) изменится лишь вид м-цы A, которая примет форму Жордановой с размерами ящика, равным кратности корня.
NotaBene: Размерности матриц
х- вектор состояний системы размерности -n;
u- вектор входа системы размерности -m;
y- вектор выхода системы размерности -p;
A-матрица (n,n) состояний;
B-матрица (n,m) связи вход-состояние;
C-матрица (p,n) связи состояние-выход;
D-матрица (p,m) связи вход-выход.
Б) Запись уравнений состояний для системы звеньев.
Пусть схема моделирования имеет вид
,где x(i) –вектор состояния i-ого звена; u(i),y(i)-одномерный вход/выход i-ого звена.u(i)-одномерный внешний вход i-ого звена.
Для записи общего уравнения состояния вводят матрицу соседства Г, определяющую связь входа i-ого звена с выходом j-ого. Тогда уравнение состояний системы примет вид: (***)
,где
x-объединенный вектор
состояний
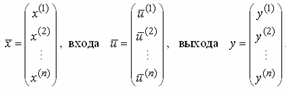
Но! Система (***) верна лишь в случае отсутствия прямых связей вход-выход для каждого звена. В противном случае, следует прейти к описанию звеньев дифференциальными уравнениями, затем, учитывая связи между звеньями, объединить все уравнения в одну систему, ввести объединенный вектор состояний, исключить промежуточные переменные и составить матрицы A,B,C,D для уравнений состояний.
Часто при рассмотрении уравнения систем состояний его приводят к нормальной форме, в котором матрица A имеет жорданов вид. Переход к нормальной форме осуществляется выполнением преобразования подобия, а именно заменой x=Mq, где М- модальная матрица(составлена из столбцов пропорциональных собственным векторам матрицы A). Преобразование приводит систему к виду :
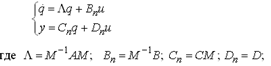
Причем матрица Λ – жорданова матрица, которая в случае отсутствия кратных корней является диагональной, в противном случае-недиагональной.
Опыт
В нашем случае мы имеем многосвязную сложную систему. Поэтому запишем уравнения состояний для отдельных блоков, а затем, устанавливая связи между состояниями в соответствии со схемой, выпишем уравнения состояний системы в целом. В реализации поставленной задачи нам помогают такие библиотечные функции CC, как CCF, OCF, DCF. Результаты выполнения команд различны, но соответствуют одной и той же системе.
Первоначально обозначим входы и выходы звеньев:
А) Для первого звена имеем:
,
вход
,
выход
,
порядок
В СС:
CC>ccf(w1)
ans.a = -18
ans.b = 1
ans.c = 2
ans.d = 0
,т.е.
,
,
,
,
И уравнения состояния для звена имеют вид:
(а*)
Б)Для второго звена:
,
вход
,
выход
,
порядок
В CC:
CC>ccf(w2)
ans.a =
0 1
-7 -5
ans.b =
0
1
ans.c =
4 0
ans.d = 0
, т.е.
,
,
,
И уравнения состояний:
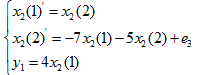(б*)
,где x2(1) и x2(2)-состояния для второго звена.
В)Для третьего звена:
,
вход
,
выход
,
порядок
В CC:
CC>ccf(w3)
ans.a = -2
ans.b = 1
ans.c = 4
ans.d = 0
, т.е.
,
,
,
,а уравнения состояний:
(в*)
Г)Учитываем связи между входами и выходами звеньев:
Выходы сумматоров e1,e3,e4 равны:
(д*)
Тогда имеем:
(е*)
Введём векторы состояний, входа и выхода:
И приведём систему к виду:
(ж*)
С учетом (а*),(б*),(в*),(е*) имеем:
z[1]’=-18z[1]+v[1]-4z[2]
z[2]’=z[3]
z[3]’=-7z[2]-5z[3]+2z[1]+4z[4]
z[4]’=-2z[4]+v[2]-4z[2]
y[1]=4z[2]
y[2]=4z[4]
Т.е Матрицы в (ж*) имеют вид:
