Санкт-Петербургский государственный политехнический университет

Факультет технической кибернетики

Кафедра компьютерных систем и программных технологий

Отчёт по расчетному заданию №1

Многокритериальная оптимизация

по курсу

Методы оптимизации

Работу выполнил студент группы № 5081/12 Бойцев Андрей Сергеевич

Работу принял преподаватель ________ Сиднев Александр Георгиевич

Санкт-Петербург

2012

Задание

Цех предприятия должен изготовить 100 изделий трёх типов. Каждого изделия нужно сделать не менее 20 штук. На изделия уходит соответственно 4, 3.4 и 2 кг металла при его общем запасе 340 кг, а также по 4.75, 11 и 2 кг пластмассы при её общем запасе 700 кг. Время изготовления изделий составляет 15, 10 и 5 минут соответственно. Вследствие различной формы изделий затраты на транспортировку всей партии определяются по формуле f = х₁ + х₂­­­­­­² + х₃­². Сколько изделий каждого типа х₁ , х₂ и х₃ надо выпустить для получения максимального выпуска в денежном выражении, если цена изделия составляет по калькуляции 40, 30 и 20$, при минимизации затрат на транспортировку и минимизации общего времени изготовления продукции?

Пункты расчетного задания.

1. Осуществить переход от многокритериальной задачи к однокритериальной с использованием следующих подходов:

А) Выделение главного критерия

Б) Свертка критериев

В) Максимин или минимакс (он же метод максиминной свертки)

Г) Метод последовательных уступок

Д) fgoalattain

2. Решить задачу стохастического программирования для одной из однокритериальных задач, превратив детерминированное ограничение в вероятностное по схеме

Менять в следующем диапазоне

Разрешается изменить формулировку исходной задачи, придумать собственную задачу, найти другую аналогичную задачу, которая могла бы быть сформулирована как многокритериальная.

Решение

Экономико-математические методы задачи:

х₁ – количество изделий первого типа, х₂ – второго типа, а х₃ – третьего типа.

Целевые функции будут иметь вид:

Прибыль: f₁ = 40x₁ + 30x₂ + 20x₃ → max

Общее время изготовления продукции: f₂ = 15x₁ + 10x₂ + 5x₃ → min

Затраты на транспортировку: f₃ = x₁ + x₂² + x₃² → min

Ограничениями задачи будут:

по общему количеству изготовленных изделий: x₁ + х₂ + х₃ = 100

по минимальному количеству каждого типа изделий: x₁ ≥ 20, x₂ ≥ 20, x₃ ≥ 20

по количеству металла для изготовления: 4x₁ + 3,4х₂ + 2х₃ ≤ 340

по количеству пластмассы для изготовления: 4,75x₁ + 11х₂ + 2х₃ ≤ 700

Приведенные неравенства можно представить следующим образом:

где

Приведенные равенства можно представить следующим образом:

где

1. Осуществление перехода от многокритериальной задачи к однокритериальной с использованием следующих подходов:

А) Выделение главного критерия

В данном методе выбирается один из критериев, например С_i, который наиболее полно отражает цель принятия решений. Остальные критерии учитываются только с точки зрения возможного указания их нижних границ С_j(a) ≥ γ_i, j i. Таким образом, исходная задача многокритериального принятия решений заменяется однокритериальной задачей с критерием C_i, т.е.

при ограничениях

За главный критерий в данной задаче необходимо взять прибыль (f₁). Следовательно, для оставшихся целевых функций необходимо указать нижние границы. Предположим, что общее время изготовления продукции (f₂) должно быть более 800 часов, а затраты на транспортировку должны превышать 1032. Данные величины были получены путем вычисления оптимального решения задачи для 2-го и 3-го критериев в отдельности. Откуда взяты предельные значения двух оставшихся показателей? Таким образом, к задаче добавляются еще 2 ограничения:

15x₁ + 10x₂ + 5x₃ ≥ 800 (1)

x₁ + x₂² + x₃² ≥ 1032 (2)

Решение задачи представлено как программа в среде Matlab, с использованием функции fmincon (Листинг 1).

Листинг 1. Метод главного критерия

% Исходные данные

x0=[20;20;20];

%%f1=40*x(1)+30*x(2)+20*x(3) -> max

%%f2=15*x(1)+10*x(2)+5*x(3) -> min

%%f3=x(1)+x(2)*x(2)+x(3)*x(3) -> min

A=[-1 0 0; 0 -1 0; 0 0 -1; 4 3.4 2; 4.75 11 2]

b=[-20; -20; -20; 340; 700]

Aeq=[1 1 1]

beq=[100]

[x2, f2] = fmincon(inline('15*x(1)+10*x(2)+5*x(3)'), x0, A, b, Aeq, beq)

[x3, f3] = fmincon(inline('x(1)+x(2)*x(2)+x(3)*x(3)'), x0, A, b, Aeq, beq)

%%

A=[-1 0 0; 0 -1 0; 0 0 -1; 4 3.4 2; 4.75 11 2; -15 -10 -5]

b=[-20; -20; -20; 340; 700; -800]

Aeq=[1 1 1]

beq=[100]

[x, fval] = fmincon(inline('-(40*x(1)+30*x(2)+20*x(3))'), x0, A, b, Aeq, beq, [], [], @mycon)

function [c, ceq] = mycon(x)

c = -(x(1)+x(2)*x(2)+x(3)*x(3)-1032); %x(1)+x(2)*x(2)+x(3)*x(3)>=1032

ceq = 0;

Из листинга 1 видно, что изменилась матрица А и b. В каждую из них была добавлена

строка, отвечающая за неравенство (1). Так как неравенство (2) является нелинейным, то для его реализации потребовалось создание функции mycon.

Функция fmincon находит минимум для скалярной функции нескольких переменных с ограничениями начиная с начального приближения (переменная x0). Так как для f₁ необходимо найти максимум, то в fmincon передается –f₁.

После выполнения программы были получены следующие результаты:

x =

56.0000

20.0000

24.0000

fval = 3320

Таким образом, для получения максимальной прибыли необходимо изготовить 56 штук изделия первого типа, 20 штук изделия второго типа и 24 штуки изделия третьего типа.

Б) Свертка критериев

Свертка критериев имеет вид:

здесь .

Так же справедлива формула с нормированными критериями:

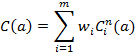
здесь , где - оптимальное решение задачи по каждому критерию в отдельности.

Решение задачи представлено как программа в среде Matlab, с использованием функции fmincon (Листинг 2).

Листинг 2. Свертка критериев

% Исходные данные

x0=[20;20;20];

%%f1=40*x(1)+30*x(2)+20*x(3) -> max

%%f2=x(1)+x(2)*x(2)+x(3)*x(3) -> min

%%f3=15*x(1)+10*x(2)+5*x(3) -> min

A=[-1 0 0; 0 -1 0; 0 0 -1; 4 3.4 2; 4.75 11 2]

b=[-20; -20; -20; 340; 700]

Aeq=[1 1 1]

beq=[100]

%%

% Вычисление оптимального решения задачи для 1-го критерия

[x1, fval1] = fmincon(inline('-(40*x(1)+30*x(2)+20*x(3))'), x0, A, b, Aeq, beq)

%%

% Вычисление оптимального решения задачи для 2-го критерия

[x2, fval2] = fmincon(inline('15*x(1)+10*x(2)+5*x(3)'), x0, A, b, Aeq, beq)

%%

% Вычисление оптимального решения задачи для 3-го критерия

[x3, fval3] = fmincon(inline('x(1)+x(2)*x(2)+x(3)*x(3)'), x0, A, b, Aeq, beq)

%%

% Суммирование

[x4, F] = fmincon(inline('-((0.5*(40*x(1)+30*x(2)+20*x(3))/3320)+(0.3*(x(1)+x(2)*x(2)+x(3)*x(3))/1032)+(0.2*(15*x(1)+10*x(2)+5*x(3))/800))'), x0, A, b, Aeq, beq)

Комментарии желательно добавить

Как видно из блока «Исходные данные», матрицы А, b, Aeq и beq не изменились по сравнению с начальными. Далее происходит вычисление оптимальных решений задачи для каждого критерия в отдельности:

fval1 = 3320

fval2 = 800

fval3 = 1032

Далее в fmincon передается сумма нормированных значений (1-ый критерий делится на fval1, 2-ой на fval2, а 3-ий на fval3), каждое из которых умножено на определенный весовой коэффициент (0,5 для 1-го критерия, 0,3 для 2-го и 0,2 для 3-го).

После выполнения программы были получены следующие результаты:

x4 =

20.0000

38.2974

41.7026

F =

1.5797

Странный результат! Должно было получиться больше 0,5!

В функции свертки были перепутаны знаки

Таким образом, для получения максимальной прибыли необходимо изготовить 20 штук изделия первого типа, 38 штук изделия второго типа и 42 штуки изделия третьего типа.

Этот рез-т взят из предыдущей задачи

В) Максимин или минимакс (он же метод максиминной свертки)

Максиминная свертка имеет вид:

Решение является наилучшим, если для всех a выполняется условие , или

Решение задачи представлено как программа в среде Matlab, с использованием функции fminimax (Листинг 3).

Листинг 3. Максиминная свертка

maxmin.m

% Исходные данные

x0=[20;20;20];

%%f1=40*x(1)+30*x(2)+20*x(3) -> max

%%f2=15*x(1)+10*x(2)+5*x(3) -> min

%%f3=x(1)+x(2)*x(2)+x(3)*x(3) -> min

A=[-1 0 0; 0 -1 0; 0 0 -1; 4 3.4 2; 4.75 11 2];

b=[-20; -20; -20; 340; 700];

Aeq=[1 1 1];

beq=[100];

[x, fval] = fminimax(@funminmax, x0, A, b, Aeq, beq)

funminmax.m

function f = funminmax(x)

f(1)=-(40*x(1)+30*x(2)+20*x(3)/3320); % Нормированные критерии

f(2)=-(15*x(1)+10*x(2)+5*x(3)/800);

f(3)=-(x(1)+x(2)*x(2)+x(3)*x(3)/1032);

Так как в среде Matlab реализована только функция fminimax, которая минимизирует наихудшие значения системы функций нескольких переменных, начиная со стартовой оценки (x0), то для реализации максиминной свертки необходимо в fminimax передавать функции обратные целевым (функция funminmax). Так как оцениваемые показатели разновелики, необходимо нормировать критерии. Критерии нормированы, так же как и в предыдущем пункте.

Задача лишена смысла, поскольку здесь фигурируют разновеликие показатели!

После выполнения программы были получены следующие результаты:

x =

48.0196

31.4006

20.5798

fval =

1.0e+003 *

-2.8629 -1.0344 -1.0344

Таким образом, для получения максимальной прибыли необходимо изготовить 48 штук изделия первого типа, 31 штуку изделия второго типа и 21 штуку изделия третьего типа.

Г) Метод последовательных уступок

Для решения данной задачи была выбрана уступка = 10%. Решение задачи представлено как программа в среде Matlab, с использованием функции fmincon (Листинг 4).

Листинг 4. Метод последовательных уступок

% Max $

x0=[20;20;20];

%%f1=40*x(1)+30*x(2)+20*x(3) -> max

%%f2=15*x(1)+10*x(2)+5*x(3) -> min

%%f3=x(1)+x(2)*x(2)+x(3)*x(3) -> min

A=[-1 0 0; 0 -1 0; 0 0 -1; 4 3.4 2; 4.75 11 2];

b=[-20; -20; -20; 340; 700];

Aeq=[1 1 1];

beq=[100];

[x, fval] = fmincon(inline('-(40*x(1)+30*x(2)+20*x(3))'), x0, A, b, Aeq, beq)

%%

% Min общего времени изготовления продукции

A=[-1 0 0; 0 -1 0; 0 0 -1; 4 3.4 2; 4.75 11 2; -40 -30 -20]

b=[-20; -20; -20; 340; 700; -2988]

[x1, fval1] = fmincon(inline('15*x(1)+10*x(2)+5*x(3)'), x0, A, b, Aeq, beq)

fval = 40*x1(1)+30*x1(2)+20*x1(3)

%%

% Min затрат на транспортировку

A=[-1 0 0; 0 -1 0; 0 0 -1; 4 3.4 2; 4.75 11 2; -40 -30 -20; 15 10 5]

b=[-20; -20; -20; 340; 700; -2988; 1093.4]

[x2, fval2] = fmincon(inline('x(1)+x(2)*x(2)+x(3)*x(3)'), x0, A, b, Aeq, beq)

fval = 40*x2(1)+30*x2(2)+20*x2(3)

fval1 = 15*x2(1)+10*x2(2)+5*x2(3)

Предположим, что критерии пронумерованы в порядке убывания важности. Первый блок программы решает задачу f1 → max. Результат выполнения:

x =

56.0000

20.0000

24.0000

fval = 3.3200e+003

Затем определим величину уступки по первому критерию: Δ₁ = 3320*0,1 = 332. Вводим дополнительное ограничение f₁ ≥ 2988 (добавляется строка в матрицу А и вектор b). Далее второй блок решает задачу f₂ → min, с учетом нового ограничения, а затем высчитывает новое значение f_1. Результаты выполнения:

x1 =

32.7333

33.3333

33.9333

fval1 = 994

fval = 2988

Видно, что значение f₁ изменилось. Определим величину уступки по второму критерию: Δ₂ = 994*0,1 = 99,4. Вводим дополнительное ограничение f₂ ≤ 1093,4 (добавляется строка в матрицу А и вектор b). Далее третий блок решает задачу f₃ → min, с учетом нового ограничения, а затем высчитывает новое значение f₁ и f_2. Результаты выполнения:

x2 =

49.3400

20.0000

30.6600

fval2 = 1.3894e+003

fval = 3.1868e+003

fval1 = 1.0934e+003

Таким образом, для получения максимальной прибыли необходимо изготовить 49 штук изделия первого типа, 20 штук изделия второго типа и 31 штуку изделия третьего типа.

Д) fgoalattain

fgoalattain решает задачу достижения цели, которая является одной из формулировок задач для векторной оптимизации.

Синтаксис:

x = fgoalattain(fun,x0,goal,weight), где

fun – целевая функция,

х0 – начальные значения,

goal – целевые значения,

weight – веса.

Решение задачи представлено как программа в среде Matlab, с использованием функций fminicon и fgoalattain (Листинг 5).

Листинг 5. Функция fgoalattain

fgoal.m

% Исходные данные

x0=[20;20;20];

%%f1=40*x(1)+30*x(2)+20*x(3) -> max

%%f2=15*x(1)+10*x(2)+5*x(3) -> min

%%f3=x(1)+x(2)*x(2)+x(3)*x(3) -> min

A=[-1 0 0; 0 -1 0; 0 0 -1; 4 3.4 2; 4.75 11 2]

b=[-20; -20; -20; 340; 700]

Aeq=[1 1 1]

beq=[100]

%%

% Goal

[x1, fval1] = fmincon(inline('-(40*x(1)+30*x(2)+20*x(3))'), x0, A, b, Aeq, beq);

goal=[0 0 0]

goal(1)=-fval1;

[x2, fval2] = fmincon(inline('15*x(1)+10*x(2)+5*x(3)'), x0, A, b, Aeq, beq);

goal(2)=fval2;

[x3, fval3] = fmincon(inline('x(1)+x(2)*x(2)+x(3)*x(3)'), x0, A, b, Aeq, beq);

goal(3)=fval3;

goal;

weight = abs(goal);

[x, fval4, attainfactor] = fgoalattain(@myfu, x0, goal, weight, A, b, Aeq, beq)

myfu.m

function [ F ] = myfu( x )

F = [40*x(1)+30*x(2)+20*x(3); 15*x(1)+10*x(2)+5*x(3); x(1)+x(2)*x(2)+x(3)*x(3)];

Сначала происходит заполнение вектора goal предельными значениями критериев. Затем weight берутся как модули goal. Функция myfu возвращает вектор, состоящий из 3-х элементов, каждый из которых содержит значение целевой функции. Результаты выполнения:

x =

49.0528

20.0000

30.9472

fval4 =

1.0e+003 *

3.1811

1.0905

1.4068

attainfactor = 0.3632

Так как attainfactor – положительный, то цели (goal) не достигнуты. Таким образом, для получения максимальной прибыли необходимо изготовить 49 штук изделия первого типа, 20 штук изделия второго типа и 31 штуку изделия третьего типа.