Натуральні рівняння кривої

Вище ми довели, що з кожною точкою регулярної кривої можна зв’язати два поняття:

• кривизну

• скрут

Виникає питання: з якою ж точністю вказані дві величини характеризують криву лінію?

Відповідь дає така теорема:

Якщо дано дві криві та , які мають однакові довжини і у відповідних точках, мають однакову кривизну і скрут, то існує переміщення, яке переводить лінію у .

Із теореми маємо, що кривизна і скрут визначають криву з точністю до положення у просторі.

З іншого боку, якщо дано дві функції , причому , то завжди існує крива для якої ці дві величини будуть кривизною і скрутом.

Виходячи із всього сказаного рівняння:

називаються натуральними рівняннями кривої

Якщо крива задана звичайною параметризацією ( ), то для того щоб написати натуральні рівняння кривої визначаємо спочатку кривизну і скрут, і тоді переходимо в отриманих виразах до натуральної параметризації.

Формули Френе

Нехай крива лінія задана в натуральній параметризації , тоді має місце така теорема:

Для всякої регулярної, принаймні тричі неперервно-диференційовної кривої мають місце рівності (формули):

(1) – Формули Френе

Доведення:

Формули Френе виражають співвідношення між векторами , , і їх похідними по параметрах аргументу.

1. перша формула випливає із теореми про існування кривизни:

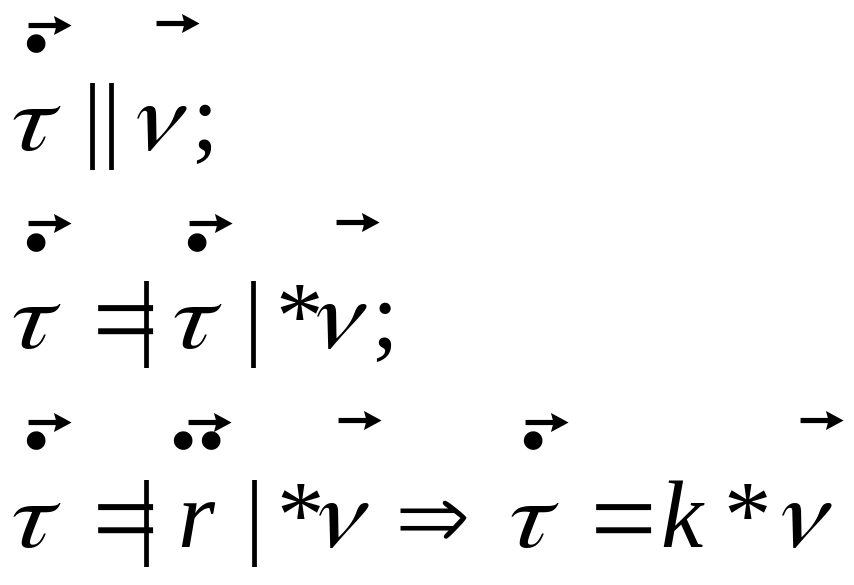
2. друга формула випливає із теореми про існування скруту:

знак “-” ставимо тому що в просторі введено праву систему координат

3)

Плоскі криві

Лінія називається плоскою якщо всі її точки належать одній і тій же площині.

На плоскі криві можна розширити ряд понять по аналогії для просторових кривих. Наприклад можна ввести поняття дотичної до плоскої кривої, як граничне положення січної.

Нехай задано плоску лінію і припустимо, що вона належить одній з координатних площин, наприклад xOy, тоді

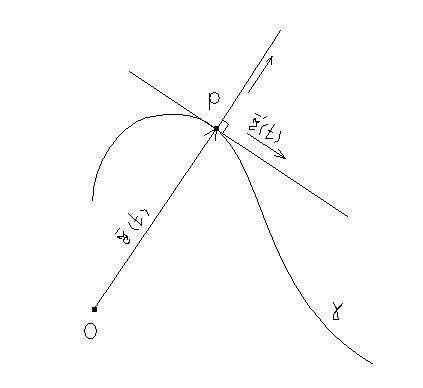, тому

Напишемо канонічне рівняння дотичної:

- канонічне рівняння дотичної

Пряма, яка проходить через т. Р кривої, перпендикулярно до дотичної, називається нормаллю.

- канонічне рівняння нормалі

вони будуть ортогональні:

Ax+By+C=0

Обчислимо кривизну даної плоскої кривої:

ЗАУВАЖЕННЯ: натуральні рівняння плоскої кривої мають вигляд:

Введемо поняття радіуса і центра кривизни даної плоскої кривої:

Радіусом кривизни кривої будемо називати величину обернену до кривої:

Розглянемо і зафіксуємо т. Р₀ , в ній побудуємо нормаль

(перпендикулярну до дотичної), і від т. Р₀, в напрямку вгнутості, відкладемо на нормалі відрізок (радіус), отримаємо т. О –центр кривизни кривої.

Аналогічну процедуру можна провести з будь-якою точкою кривої .

Геометричне місце центрів кривизни кривої називається еволютою даної кривої.

Евольвентою даної кривої називається крива лінія, по відношенню до якої дана лінія є еволютою.

Поверхні в трьохвимірному евклідовому просторі

Векторні функції двох скалярних аргументів

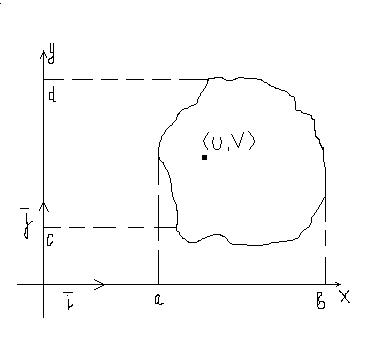Розглянемо в просторі деяку двохвимірну область: [a,b]*[c,d]=D

Кожна точка цієї області характеризується парою дійсних чисел U та V;

Векторною функцією двох скалярних аргументів U та V називається відповідність (відображення) при якій точці області D ставиться у відповідність вектор трьохвимірного евклідового простору .

Границя векторної функції двох скалярних аргументів

Сталий вектор називається границею векторної функції при , якщо виконується умова

Теорема:

Якщо існують границі

то мають місце рівності:

1)

2)

3)

4)

Доведення: (аналогічне).

Поняття неперервності векторних функцій

двох скалярних аргументів

Векторна функція двох змінних називається неперервною в точці , якщо границя функції дорівнює значенню функції в даній точці

Векторна функція називається неперервною в області Д, якщо вона непевна в кожній точці цієї області.

Векторна функція називається непевною, якщо вона є непевною на всій області визначення.

Похідна векторної функції двох скалярних аргументів

Нехай дано векторну функцію двох скалярних аргументів , зафіксуємо в ній змінну V=V₀ ,

Похідна векторної функції по параметру U називається частинною похідною векторної функції по параметру U ; .

Похідна векторної функції по параметру V називається частинною похідною векторної функції по параметру V ; .

Вектор функції двох скалярних аргументів в координатах

Розглянемо вектор функцію в базисі , тоді цю функцію можна розкласти по базисних векторах: , тому

Теорема:

Для того, щоб сталий вектор з координатами був границею векторної функції необхідно і достатньо, щоб виконувались співвідношення:

Доведення: аналогічне до теореми векторної функції одного скалярного аргументу.

Для того щоб функція була диференційованою потрібно щоб були диференціали , тобто

Поняття поверхні в просторі

Параметричні рівняння поверхонь

Розглянемо в просторі область Д

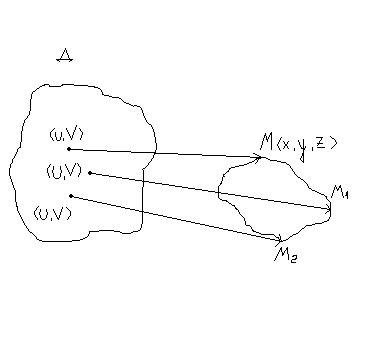
Область Д називається елементарною, якщо вона є гомеоморфною відкритому кругу.

Будемо відображати всі точки області Д задапомогою гомеоморфного відображення у простір, отримаємо геометричне місце точок, яке буде елементарною поверхнею.

Елементарною поверхнею втрьох вимірному евклідовому просторі називається геометричне місце точок простору, яке є образом елементарної області при гомеоморфному відображенні її у простір.

- параметричні рівняння елементарної поверхні (1)

домножимо кожну із рівностей (1) відповідно на і додамо, маємо:

- векторне рівняння поверхні (2)

Припустимо, що в рівностях (1), наприклад 1 і 2 рівняння ми змогли розв’язати відносно U та V, тоді U та V будуть функціями від x та y, підставимо вирази для U та V в третє рівняння:

(3)

поверхню можна задати рівнянням в неявному вигляді:

(4)

Поверхнею у просторі називається геометричний образ, яки складається з численного числа елементарних поверхонь.

ЗАУВАЖЕННЯ: в дальнішому нас повністю задовольнятиме поняття елементарної поверхні.

Поверхня називається к-регулярною, якщо к-регулярними є функції x, y, z із рівняння (1).