
- •Векторні функції скалярного аргументу і їх властивості
- •Границя векторних функцій
- •Tеорема:
- •Доведення:
- •Неперервність векторних функцій
- •Векторна похідна
- •Елементи тригранника Френе
- •Дотична до кривої
- •Теорема:
- •Доведення:
- •Нормальна площина кривої
- •Бінормаль кривої
- •Спрямна площина
- •Головна нормаль
- •Довжина дуги кривої Натуральна параметризація
- •Кривизна кривої
- •Теорема:
- •Доведення:
- •Натуральні рівняння кривої
- •Формули Френе
- •Доведення:
- •Плоскі криві
- •Лінія на поверхні
- •Дотична площина і нормаль до поверхні
- •Перша квадратична форма поверхні
- •Застосування першої квадратичної форми
- •Друга квадратична форма поверхні
- •Кривизна кривої на поверхні Нормальна кривизна поверхні Теорема Меньє
- •Теорема Меньє
- •Нормальна кривизна поверхні в даному напрямку є величина стала.
- •Геодезична кривизна і її обчислення
- •Головні кривизни на поверхні
- •Індикатриса кривизни Дюпена
- •Класифікація точок на поверхні:
- •Класифікація точок на основі поняття ідекатриси Дюпена
- •Класифікація точок поверхні на основі поняття Гаусової (повної) кривизни поверхні
- •Класифікація точок з використанням поняття стичного параболоїда поверхні
- •Поверхня обертання і її рівняння
- •Головні напрямки на поверхні
- •Асимптотичні напрямки на поверхні Асимптотичні лінії
- •Геодезичні напрямки на поверхні
- •Сферичне зображення області на поверхні Теорема Гауса
- •Теорема :
- •Ізометричні поверхні Згинання поверхні
- •Теорема Гауса-Бонне(без доведення)
- •Теорема Гауса-Бонне:
- •Топологічний простір
- •I. Об'єднання будь-якої кількості (скінченної або нескінченної) відкритих множин є відкрита множина.
- •II. Перетин будь-яких двох відкритих множин є відкрита множина.
- •Топологічні перетворення і їх властивості
- •Замкнені множини Граничні точки
- •3°. Перетин будь-якої системи (скінченої чи нескінченної) замкнених множин є замкнена множина.(якщо - сукупність замкнених множин, то множина замкнена).
- •4°. Множина м простору замкнена тоді і тільки тоді, коли вона містить всі свої граничні точки.
- •Кліткове розбиття поверхні Орієнтовні поверхні
- •Теорема Ейлера для многогранників
- •Приклади топологічно правильних многогранників
- •Топологічні властивості проективної площини
Елементи тригранника Френе
Нехай
у просторі задано деяку регулярну криву
![]() ,
зафіксуємо на ній деяку точку Р. З точкою
Р, регулярної кривої, можна зв’язати
такі елементи:
,
зафіксуємо на ній деяку точку Р. З точкою
Р, регулярної кривої, можна зв’язати
такі елементи:
три криві:
-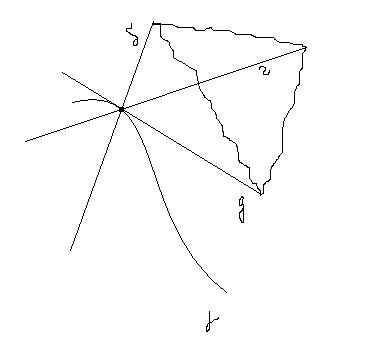 дотичну
дотичну
- бінормаль
- головну нормаль
три площини:
- стична
- нормальна
- спрямна
Тригранником Френе кривої, у даній точці, називається конфігурація, яка складається із трьох прямих (дотичної, бінормалі, головної нормалі) і трьох площин (стичної, нормальної, спрямної).
Інколи його називають супроводжуючим тригранником кривої.
Дотична до кривої
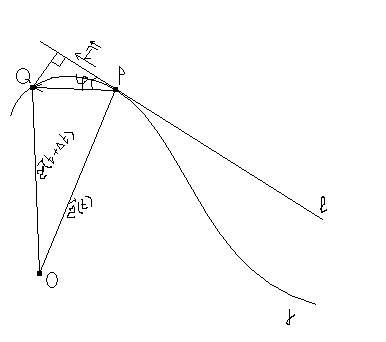 Будемо
розглядати у просторі криву лінію
,
задану векторним рівнянням.
Будемо
розглядати у просторі криву лінію
,
задану векторним рівнянням.
![]() (1)
(1)
т.Q- нескінченно близька до т.P
|PQ|=d - довжина
![]() (Q,l)=h
– відстань
(Q,l)=h
– відстань
Дотичною до кривої в т. Р називається пряма,яка проходить через т.Р,кривої, і для якої виконується така умова:
![]() (2)
(2)
Теорема:
Всяка гладка крива у кожній своїй точці має дотичну, причому єдину.
Якщо
![]() -
векторна параметризація кривої, то
дотична паралельна до вектора
-
векторна параметризація кривої, то
дотична паралельна до вектора
![]()
Доведення:
П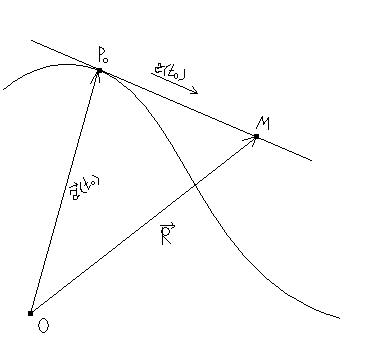 рипустимо,
що пряма l
є дотичною до кривої (1) в т.Р.
рипустимо,
що пряма l
є дотичною до кривої (1) в т.Р.
Покажемо, що ця дотична паралельна до вектора . Для цього скористаємось означенням дотичної, тобто рівністю (2).
Нехай
вектор
![]() - одиничний вектор, паралельний до
дотичної |
|=1
- одиничний вектор, паралельний до
дотичної |
|=1
|PQ|=d
кут між
векторами
![]()
![]()
Нехай т.О – початок просторової координат (полюс)
Тоді
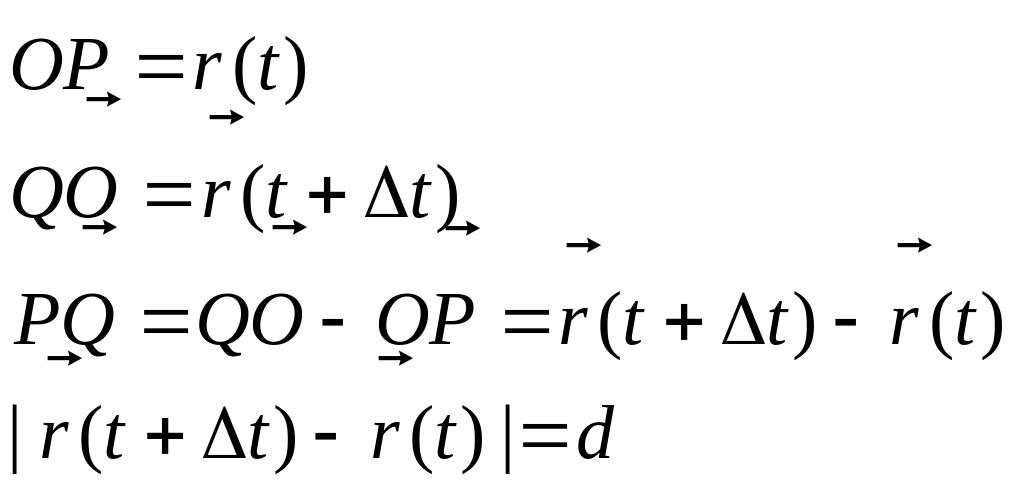
Для знаходження h розглянемо модуль векторного добутку:
![]()
отже
h=![]()
Скористаємось рівністю (2):
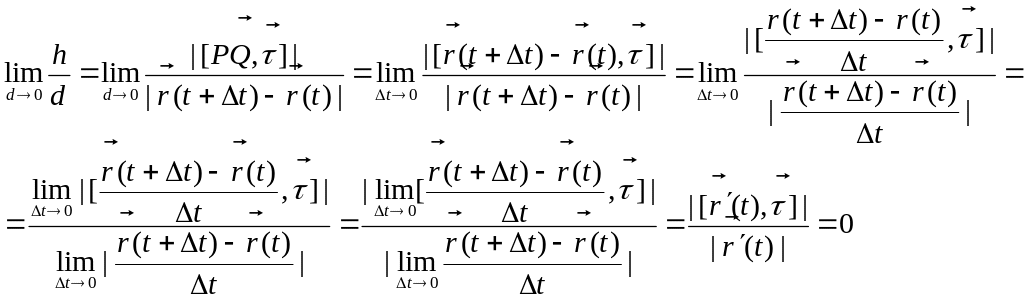
Звідси
випливає,що
![]() вектор
колінеарний до вектора
, вектор
колінеарний до дотичної, отже і
колінеарний до дотичної.
вектор
колінеарний до вектора
, вектор
колінеарний до дотичної, отже і
колінеарний до дотичної.
Єдиність дотичної випливає з того, що для похідна єдина.
Покажемо тепер, що всяка пряма, яка проходить через т.Р кривої, і паралельна до вектора є дотичною, тобто для неї виконується рівність (2).
![]() =0,
так як вектор
||
=0,
так як вектор
||
Знайдемо тепер рівняння дотичної для різних способів параметризації кривої
1)
Нехай крива лінія
задана векторним рівнянням
![]() (1)
(1)
побудуємо дотичну у т.Р0
візьмемо довільну т.М
![]()
З
![]() маємо:
маємо:
![]() (3)
(3)
![]() підставивши
в (3), отримаємо:
підставивши
в (3), отримаємо:
![]() -
векторно-параметричне рівняння дотичної
-
векторно-параметричне рівняння дотичної
2) Нехай тепер лінія задана параметрично (5)
нехай
т.М (x,y,z),
тоді і вектор
![]()
![]()
з рівності (4) отримаємо
![]() (6) –
параметричні рівняння дотичної
(6) –
параметричні рівняння дотичної
3)
Припустимо,
що
задана рівнянням
![]()
визначивши
у кожному з рівнянь (6)
![]() матимемо:
матимемо:
![]() (7)-
канонічне рівняння дотичної
(7)-
канонічне рівняння дотичної
Нехай тепер крива лінія задана так:
(8)
припустимо,що наша лінія задана параметрично:
тоді рівняння лінії запишеться так:
![]() (9)
(9)
продиференціюємо по t
![]()
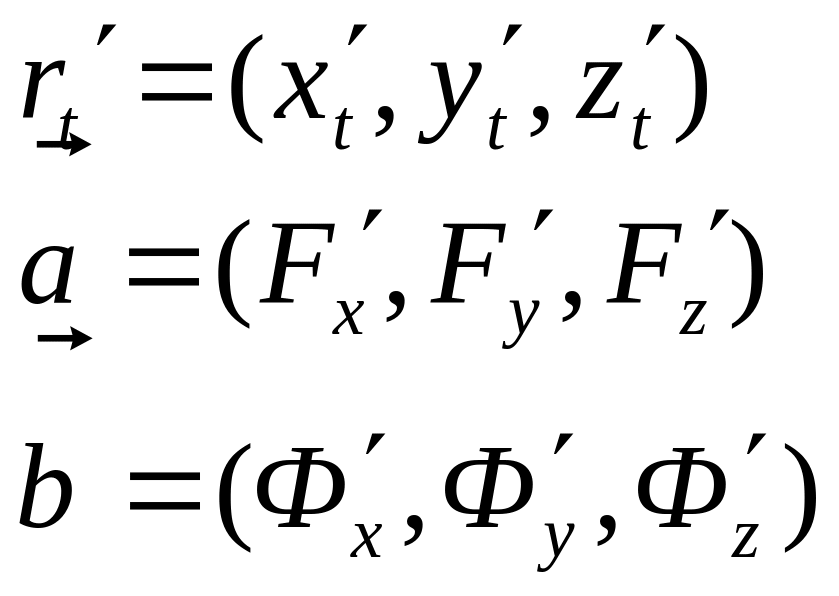
![]()
отже за напрямний вектор дотичної в даному випадку можна прийняти векторний добуток векторів a і b
![]()
-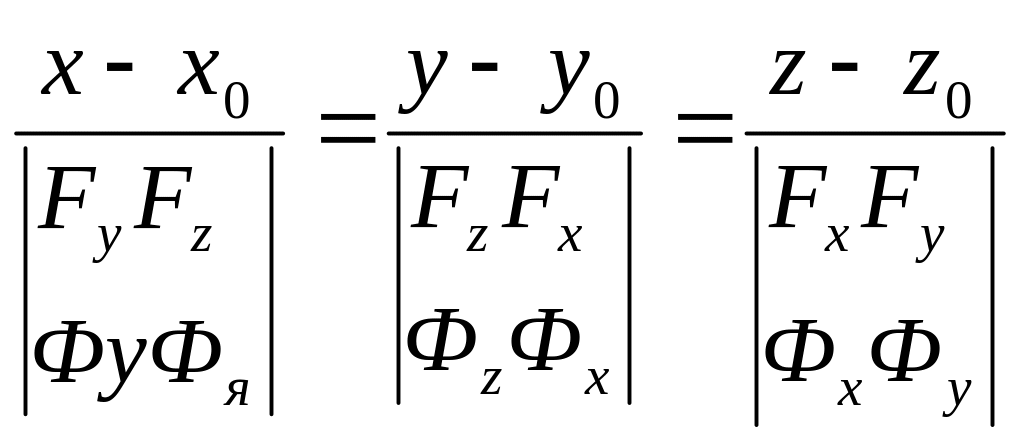 канонічне
рівняння дотичної
канонічне
рівняння дотичної
